Todo lo visible oculta algo invisible.
En Los paseos de Euclides (1955), el pintor surrealista René Magritte (1898-1967) representa un caballete con un cuadro situado frente a una ventana a través de la cual se observa un paisaje urbano. La escena pintada corresponde exactamente al fragmento de paisaje sobre el que se sitúa el cuadro. ¿O quizás no?

No es la única propuesta paradójica de «lienzo sobre lienzo» (o de «paisaje frente a una ventana rota») del pintor. Desde la primera mirada al cuadro se provoca la incertidumbre: ¿qué parte es real y qué parte está pintada? ¿El lienzo oculta parte de esa realidad, la altera, o la reproduce con exactitud? ¿Acaso el pintor camufla tras el lienzo situado dentro del cuadro una situación que ha decidido transformar?
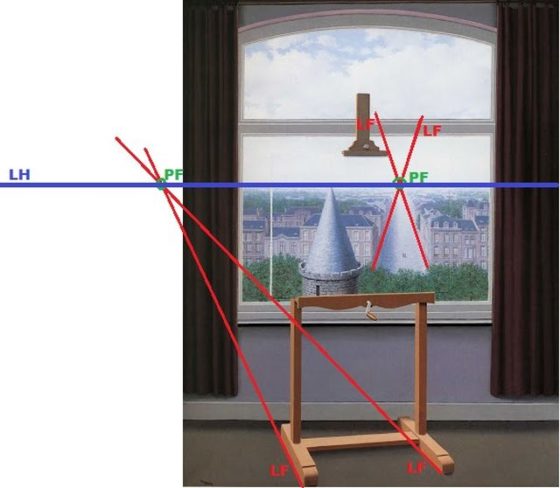
¿Y por qué Magritte hace referencia a Euclides (ca. 325 a. C.-ca. 265 a. C.) en el título de su cuadro? Aunque el geómetra no aparece en el lienzo, el cuadro contiene algunas ilusiones ópticas provocadas por formas geométricas y por ciertos efectos de la perspectiva.
En esta pintura el autor superpone exactamente el cuadro situado en la habitación sobre el paisaje real que se puede divisar a través de la ventana. Debido a este solapamiento, la imagen del cuadro se prolonga en el paisaje que se encuentra a su alrededor.
A la izquierda del lienzo, una línea blanca marca un tenue corte que separa la imagen del cuadro de su extensión a la imagen real. Además, en la parte superior derecha, una ligera diferencia de brillo actúa también como elemento separador.
A pesar de que el caballete puede pensarse como una manera de diferenciar el cuadro del paisaje exterior, también puede verse como un elemento integrador: se apoya en el suelo de la habitación (una estancia oscura, poco iluminada), se pone en contacto con él, y después se eleva verticalmente, se conecta en continuidad con el lienzo que soporta y a través de él se prolonga en el paisaje exterior (que contrasta con el interior por su gran claridad). ¿Qué está dentro de la habitación y qué está fuera?
Una segunda ilusión óptica hace percibir un cono que en realidad no está dibujado. La larga avenida situada entre las casas se asemeja al tejado cónico de la torre situada a su izquierda. Aunque no se confunden; ¿la vía parece quizás un tejado inacabado de una torre que en realidad no existe?
La perspectiva de la obra también produce un cierto desconcierto. El cuadro con su caballete tiene una ligera inclinación, como lo muestra el ángulo entre el alféizar de la ventana y la tabla inferior del caballete: el paisaje visto por la ventana se contempla de frente y el del cuadro se observa de manera oblicua. aunque los dos ángulos de visión no tienen nada que ver entre sí y corresponden a imágenes diferentes, sincronizan con precisión.
Finalizamos sin olvidar a Magritte; porque esto no es una «pi», es una aproximación de pi. De hecho, es la mejor aproximación de pi que se puede encontrar en el calendario. ¿Por qué? Porque 22/7 = 3,14285714… es una buena aproximación del número pi, el día que más «se acerca» a su valor durante todo el año (al dividir el número del día entre el número del mes). Por este motivo, el 22 de julio se celebra el Casual Pi Day (Día de aproximación de Pi), una de esas inocentes excentricidades que divierten a gran parte de la comunidad matemática.

Referencias
- Magritte : les promenades d’Euclide, Quator, 8 octubre 2006
- Marta Macho Stadler, Los paseos de Euclides, ZTFNews, 21 noviembre 2013
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
