Como escribí en mi anterior entrada del Cuaderno de Cultura Científica, titulada Geometría en los pavimentos romanos cosmatescos, observando el hermoso pavimento de la Basílica de Santa María en Cosmedin en Roma, en la cual se encuentra la Boca de la Verdad, me llevé algunas sorpresas.

Una de esas sorpresas, además de las mencionadas en mi anterior entrada, fue que en parte de ese pavimento de estilo cosmatesco pude observar el triángulo fractal de Sierpinski, o, para ser más preciso, una estructura geométrica que me recordaba claramente al triángulo de Sierpinski. En concreto, en este pavimento, que os muestro en la siguiente imagen, observé que la mitad de las baldosas triangulares del mosaico estaban formadas por un triángulo equilátero dividido en cuatro triángulos equiláteros, de los cuales el central estaba dotado de color, mientras que los otros tres apoyados en los vértices, estaban divididos de nuevo en cuatro triángulos equiláteros, con color solamente los pequeños triángulos centrales.

Aunque la mayor sorpresa en mi viaje a Roma, en relación con esta estructura geométrica, me la encontré en el suelo de la Basílica de Santa María en Trastevere (siglo XII). Al entrar en el interior de esta basílica romana uno descubre tanta belleza geométrica que no sabe a dónde mirar. Entre todas las bellezas del pavimento, también de estilo cosmatesco, se encontraba esta que os muestro a continuación y que es una versión más compleja aún del triángulo fractal de Sierpinski “romano”.

Pero expliquemos qué es eso del triángulo fractal de Sierpinski. Este objeto fractal (véase la entrada Fractus, arte y matemáticas para saber qué es un fractal) debe su nombre al matemático polaco Waclaw Franciszek Sierpinski (1882-1969). Este gran matemático del siglo XX, que escribió más de 700 artículos de investigación y 50 libros (entre ellos: Números cardinales y ordinales (1958), Introducción a la topología general (1934), Topología general (1952), Triángulos pitagóricos (1952) o Teoría elemental de números (1914 y 1959)), trabajó en teoría de conjuntos –con contribuciones al axioma de elección y la hipótesis del continuo-, teoría de números, teoría de funciones, topología y lógica matemática. Su nombre se ha asociado a algunos objetos matemáticos, como los fractales denominados curva de Sierpinski, triángulo de Sierpinski y alfombra de Sierpinski, o a los conocidos como números de Sierpinski.

El triángulo de Sierpinski es un objeto fractal introducido por el matemático Wraclaw Sierpinski en 1916. Satisface algunas de las propiedades características de los fractales: es autosemejante (es decir, al hacer zoom sobre el objeto, se observa que partes más pequeñas del objeto son exactamente, o aproximadamente, iguales a todo el objeto), se puede construir mediante un algoritmo recursivo (en este caso, a partir de un triángulo equilátero), tiene área cero (si se calcula el área del objeto en cada paso de su construcción cada vez es más pequeña y su límite es cero) y tiene dimensión no entera, de hecho, irracional (1,58496…), aunque esto necesitaría de una explicación más larga que ahora no abordaremos.

La construcción es la siguiente. En el primer paso se considera un triángulo equilátero (en negro en la siguiente imagen). En el segundo paso se divide el triángulo inicial en cuatro triángulos equiláteros más pequeños de la siguiente forma. Se considera los puntos medios de los tres lados del triángulo y se unen mediante segmentos rectos, esto nos genera un triángulo central, que se elimina (por eso queda blanco en la imagen), y tres triángulos equiláteros que tocan los vértices del triángulo inicial (que se mantienen negros). En el tercer paso se realiza la misma operación para cada uno de los tres pequeños triángulos (negros) que se han mantenido, es decir, se eliminan los tres pequeños triángulos equiláteros centrales (blancos) y se mantienen los otros nueve triángulos (negros). De esta forma se continua en cada paso, dividiendo cada triángulo equilátero negro, en cuatro triángulos más pequeños y eliminando el central (blanco) y dejando los exteriores (negros), como se muestra en la siguiente imagen. El triángulo de Sierpinski es el objeto fractal que se obtiene al continuar este proceso de forma infinita.

La construcción de este fractal de Sierpinski se puede explicar de otra manera. Como antes, partimos en el primer paso de un triángulo equilátero (negro). En el segundo paso se realizan tres copias, de la mitad de altura y la mitad de anchura, del anterior triangulo y se pegan de manera que cada uno de esos tres nuevos triángulos toque a los otros dos por uno de sus vértices, como se observa en la imagen. En el tercer paso se realizaría una operación similar, pero para el objeto geométrico obtenido en el segundo paso. Y así se continua de forma infinita. Esta construcción nos da una idea de la autosemejanza de este fractal.

Como podemos observar, la imagen del pavimento de Santa María en Cosmedin se corresponde con el tercer paso de esta construcción fractal, mientras que el pavimento de Santa María en Trastevere se corresponde con el objeto geométrico tras cinco pasos. Claramente los artesanos romanos que construyeron estos maravillosos pavimentos de estilo cosmatesco, alrededor del siglo XII, no sabían qué era un fractal, pero sí eran capaces de realizar hermosas construcciones geométricas como esta.

La construcción del triángulo fractal de Sierpinski se puede realizar con cualquier otro tipo de triángulo, no necesariamente equilátero. De hecho, en la Basílica de Santa María en Cosmedin también nos encontramos la realización, hasta el tercer paso, para triángulos rectángulos isósceles (véase la siguiente imagen).

El triángulo de Sierpinski, que nos lo podemos encontrar en diferentes contextos, como el grafo asociado al rompecabezas de la torre de Hanoi (como puede verse en el libro Del ajedrez a los grafos, RBA, 2015) o los patrones geométricos del triángulo de Pascal (véase la entrada de Marta Macho Triangulando: Pascal versus Sierpinsaki, la novela El diablo de los números, de Hans Magnus Enzensberger, publicado en Siruela en 1997, o el libro La gran familia de los números, Catarata, 2021), aparece también asociado al conocido como “juego del caos”, al que vamos a dedicar la última parte de esta entrada.

Para jugar al juego del caos se necesita una hoja de papel, un lápiz, una regla y un dado, para una versión manual del mismo. Lo primero que debemos hacer es pintar tres puntos A, B, C que forman un triángulo equilátero, es decir, cada punto está a la misma distancia de los otros dos (aunque el juego funciona para cualquier tipo de triángulo).

Se empieza pintando un punto cualquiera P(0) dentro del triángulo formado por los puntos A, B y C (que hemos pintado de rojo en la imagen siguiente).

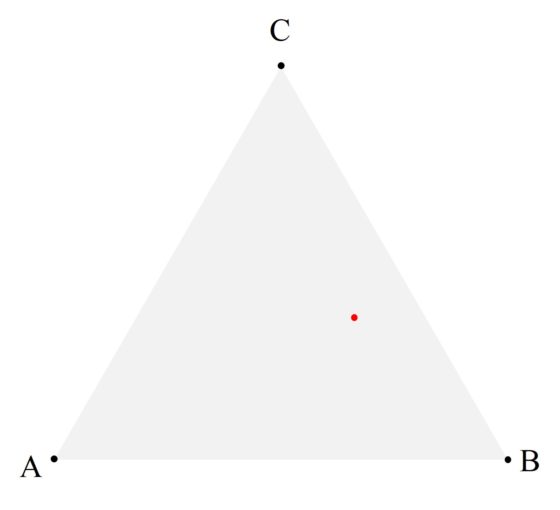
A continuación, vamos a lanzar el dado y pintaremos el siguiente punto P(1) en el triángulo en función del resultado:

i) si sale 1 o 2, entonces P(1) será el punto medio entre el punto inicial P(0) y A;

ii) si sale 3 o 4, entonces P(1) será el punto medio entre el punto inicial P(0) y B;

iii) si sale 5 o 6, entonces P(1) será el punto medio entre el punto inicial P(0) y C.

La regla se utiliza para determinar el punto medio entre los dos puntos correspondientes, en cualquiera de las tres circunstancias anteriores. Obtenido el punto P(1), tomamos este punto y calculamos el punto P(2) utilizando el mismo algoritmo anterior, pero considerando P(1) en lugar de P(0). De esta forma, se irán obteniendo los diferentes puntos P(3), P(4), etc. Es decir, obtenidos n puntos mediante este algoritmo, desde P(0) hasta P(n – 1), se calcula el punto P(n) de la misma forma a partir del punto P(n – 1). Esto es,

i) si sale 1 o 2, entonces P(n) será el punto medio entre el punto inicial P(n – 1) y A;

ii) si sale 3 o 4, entonces P(n) será el punto medio entre el punto inicial P(n – 1) y B;

iii) si sale 5 o 6, entonces P(n) será el punto medio entre el punto inicial P(n – 1) y C.

En la siguiente imagen hemos pintado los cinco primeros puntos descritos con este algoritmo, empezando en el punto rojo (que es el punto inicial P(0)), después de sacar con el dado 6, 1, 5, 4 y 1.

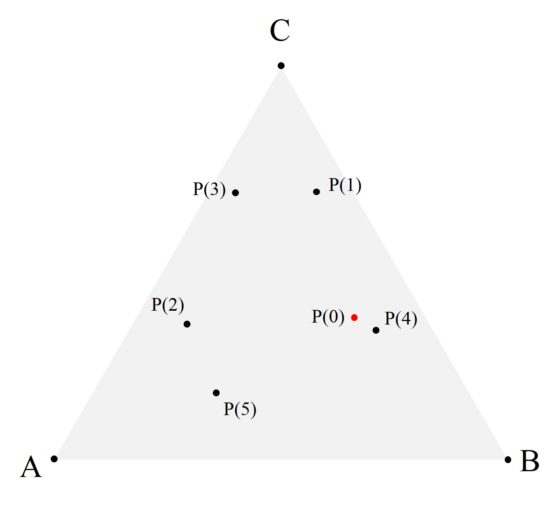
Lo sorprendente de este juego es que según se van representando cada vez más puntos mediante ese algoritmo, independientemente de cual sea el punto inicial, empieza a surgir el triángulo de Sierpinski.

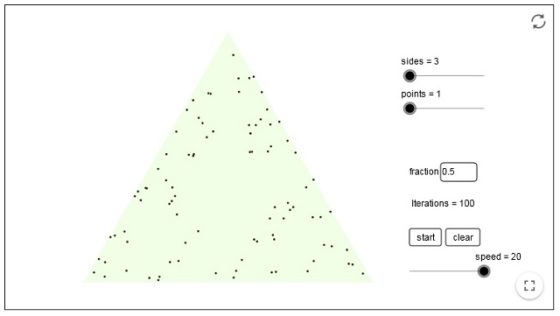
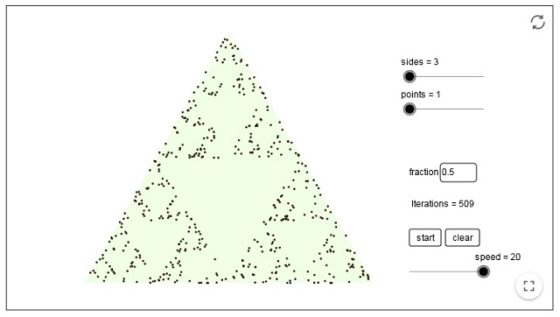
Veamos una sucesión de imágenes –obtenidas con un simulador del juego del caos realizado con Geogebra, diseñado por slik y que podéis ver aquí – que nos ofrecen los diferentes resultados del juego del caos para un determinado punto inicial, tras 100, 500, 1.000, 2.000 y 5.000 pasos.

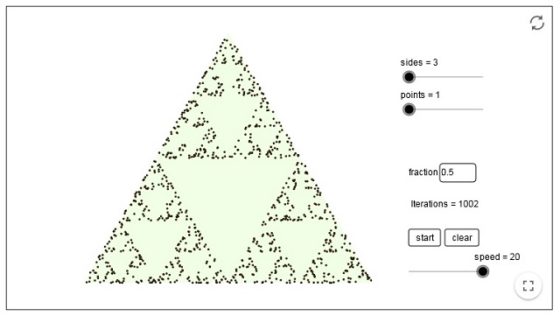
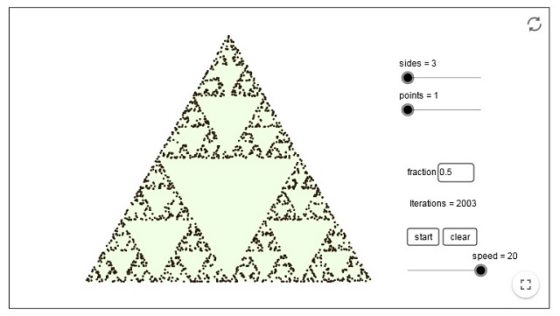
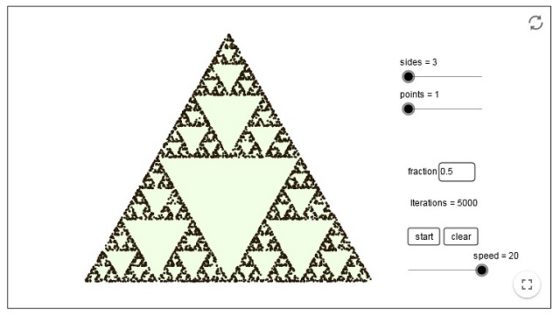
Este algoritmo fue introducido por el matemático británico Michael Barnsley en su libro Fractals Everywhere (1988) y no solo sirve para triángulos y la mitad de a distancia, sino para polígonos de n lados y una fracción de distancia r. Por ejemplo, para n = 5, sobre un pentágono, y para una fracción de distancia de r = 3/8 se obtiene el siguiente objeto fractal, tras 10.000 pasos.

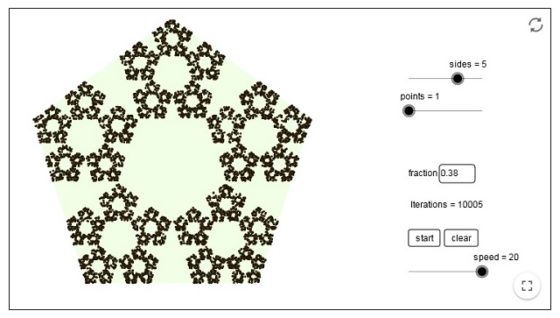
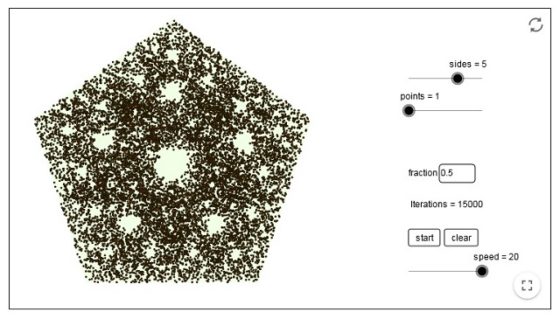
Mientras que si tomamos una fracción de distancia de r = 1/2 el resultado, tras 15.000 pasos es el siguiente conjunto.

O para n = 6, sobre un hexágono, con una fracción de distancia de r = 1/3 se obtiene el siguiente resultado tras 10.000 pasos.

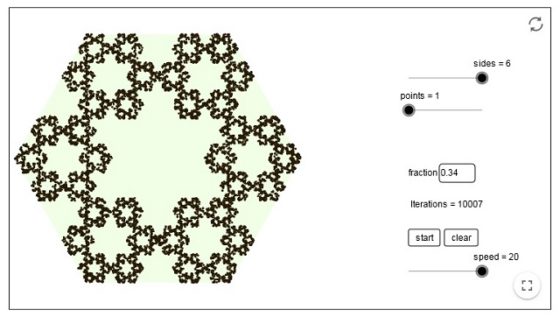
Y en esta última imagen obtenemos un nuevo fractal clásico, el copo de nieve de Koch (véase la entrada Fractus, arte y matemáticas), justo como la frontera interior del mismo.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica