Estos días estaba yo buscando información sobre los triángulos pitagóricos cuando he descubierto un curioso resultado geométrico, el conocido como primer teorema de Haga, un sencillo método para construir un triángulo pitagórico doblando una hoja de papel cuadrada. El objetivo de esta entrada del Cuaderno de Cultura Científica es explicar esta hermosa construcción.

Para empezar, recordemos que un triángulo pitagórico es un triángulo rectángulo, es decir, cuyos lados (a, b, c), siendo a y b los catetos y c la hipotenusa, no solo verifican la igualdad derivada del teorema de Pitágoras a² + b² = c² (véase la entrada Pitágoras sin palabras), sino que son números enteros, como las ternas (3, 4, 5), (5, 12, 13) o (8, 15, 17).

Aunque debemos el estudio general del resultado geométrico conocido como teorema de Pitágoras y su demostración al matemático griego Pitágoras (aprox. 585-500 a.n.e.), lo cierto es que el resultado ya era conocido anteriormente en Babilonia, Egipto, India o China, quienes desarrollaron métodos para obtener ternas pitagóricas (números naturales (a, b, c) que satisfacen la ecuación a² + b² = c²) y las utilizaron para trazar ángulos rectos en construcción y agrimensura. Por ejemplo, el método chino consistía en coger dos números u y v (el primero mayor que el segundo) y obtener la terna pitagórica mediante las expresiones:

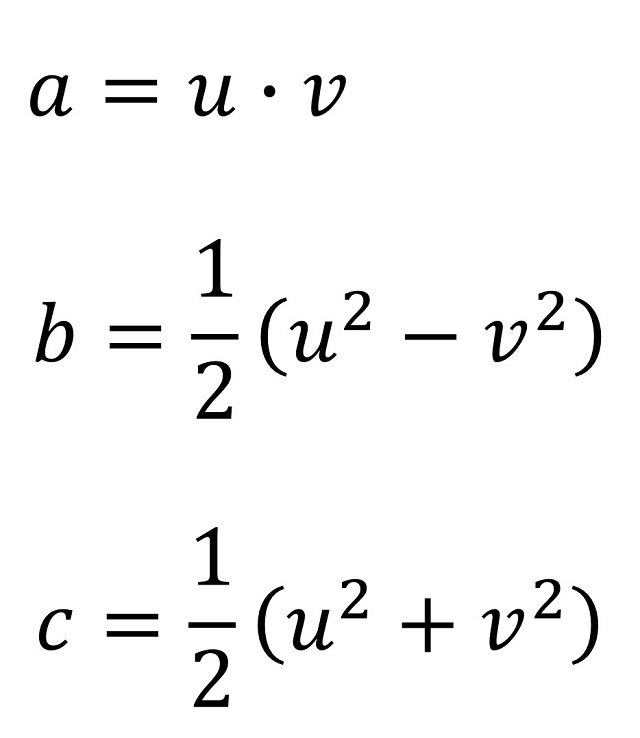
Para u = 3 y v = 1 se obtiene la terna pitagórica (3, 4, 5) que da lugar al triángulo egipcio o para u = 5 y v = 1 se obtiene la terna (5, 12, 13) cuyo triángulo rectángulo asociado se conoce como triángulo indio.

Pero vayamos con la construcción de un triángulo pitagórico doblando una hoja de papel cuadrada, el primer teorema de Haga, extraída del libro del octogenario biólogo japonés Kazuo Haga, Origamics, Mathematical Explorations through Paper Folding.

Para empezar, necesitamos una hoja de papel cuadrada. De forma natural, esto quiere decir que el plegado es reproducible, su resultado lo podemos obtener en cualquier otra hoja cuadrada, podemos doblarla de dos maneras distintas. Un plegado consiste en unir un lado del cuadrado con su opuesto lo cual da lugar a un pliegue por la mitad de la hoja, mientras que el otro consiste en unir un vértice del cuadrado con el vértice opuesto dando lugar a un plegado por la diagonal del cuadrado.

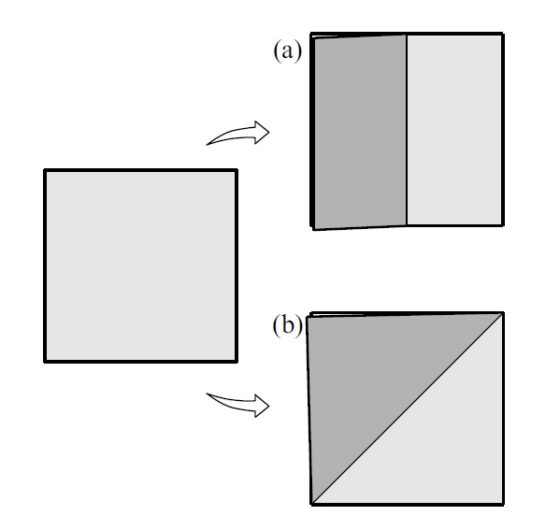
Para la construcción de Haga necesitamos marcar el punto medio de uno de los lados, lo cual se consigue fácilmente con el primer plegado comentado anteriormente, como se muestra también en la siguiente imagen (para quien quiera realizar la construcción en su casa), y después volver a desplegar la hoja volviendo a su posición cuadrada original.

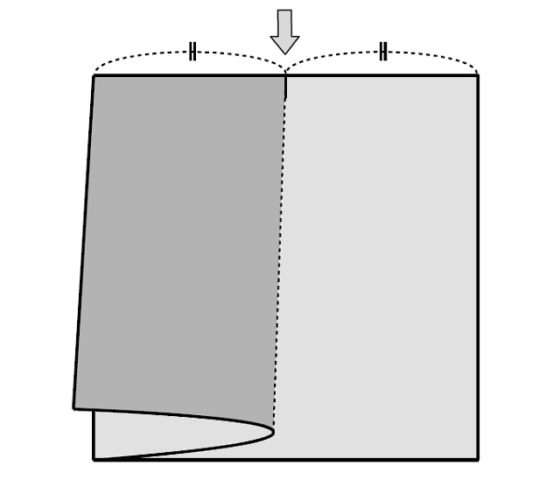
El plegado que nos va a dar lugar al triángulo pitagórico consiste en coger el vértice de abajo a la derecha, cuando tenemos la hoja cuadrada desplegada, y situarlo sobre el punto medio del lado de arriba (como se muestra en la siguiente imagen), lo cual nos genera el plegado de la hoja cuadrada sobre una línea que va desde lado izquierdo al derecho.

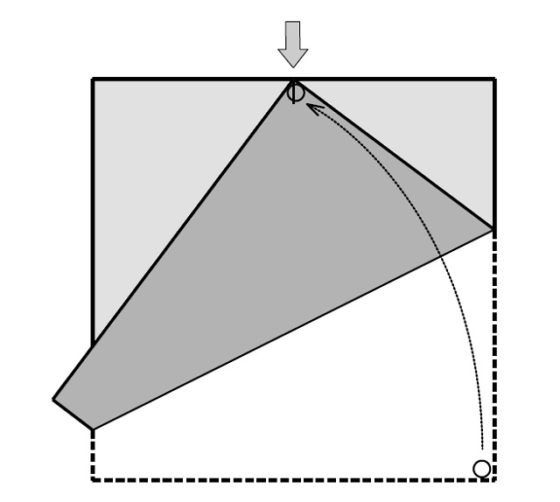
El plegado realizado es el único que se necesita, pero vamos a comprobar que hemos generado tres triángulos rectángulos cuyos lados son proporcionales al triángulo egipcio 3:4:5. Para demostrar esto vamos a marcar una serie de puntos en la figura: los vértices del cuadrado A, B, C, D (empezando arriba a la izquierda y siguiendo el sentido contrario a las agujas del reloj), el punto medio E del lado AD, los puntos F, G en los que la línea de plegado toca a los lados laterales del cuadrado y el punto H marcado por la intersección del lado CB (que se convierte al plegarse en CI) con el lado BA al ser plegado sobre el anterior.

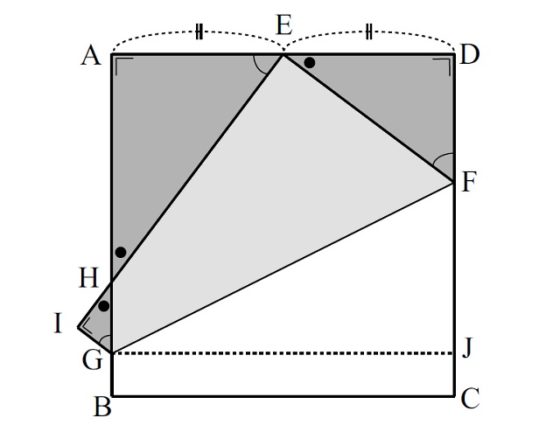
Lo primero que se podría observar en la imagen anterior es que los tres triángulos rectángulos generados sobre el papel cuadrado con el pliegue, AHE, DEF y IGH, son semejantes. Recordemos que dos triángulos son semejantes si tienen la misma forma, es decir, tienen los tres ángulos iguales, solo se diferencian por su tamaño.

Pero empecemos por el triángulo DEF y veamos que es proporcional al triángulo egipcio 3:4:5, es decir, tomando la hoja de papel cuadrada de un cierto tamaño obtendríamos el triángulo pitagórico 3:4:5. Consideremos que la longitud de los lados de la hoja de papel cuadrada es la unidad, 1. Si llamamos a (es nuestra incógnita) a la longitud del lado DF, entonces la longitud de FC es 1 – a, pero como FE = FC, por el plegado, tenemos que la hipotenusa del triángulo rectángulo DEF, el lado FE, tiene longitud 1 – a. La longitud del lado ED la conocemos, ya que E es el punto medio de AD, es 1/2. Si aplicamos ahora el teorema de Pitágoras al triángulo rectángulo DEF se tiene que

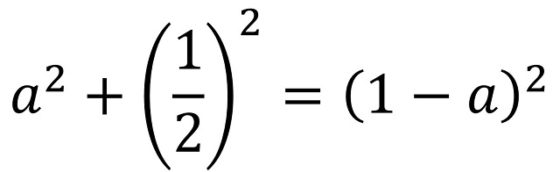
de donde se puede despejar y obtener el valor de a, que es a = 3/8. Por lo tanto, los lados del triángulo rectángulo tienen longitud 3/8, 1/2 y 5/8. Estas longitudes son proporcionales al triángulo 3:4:5, para lo cual basta multiplicar por 8, o dicho de otra forma, si el cuadrado original tiene lado igual a 8, las longitudes del triángulo rectángulo originado por esta doblez son 3, 4 y 5. ¡El triángulo pitagórico egipcio!.

Resultado 1 (teorema de Haga): el triángulo rectángulo DEF es proporcional a un triángulo pitagórico 3:4:5.

A continuación, razonemos sobre el triángulo AHE. Para empezar, el ángulo BCD, que es un ángulo recto, se ha convertido mediante el plegado en el ángulo IEF, luego también es recto. Por lo tanto, los ángulos DEF y AEH son complementarios, de donde se deduce que los triángulos DEF y AHE son semejantes, como se comentaba más arriba, es decir, uno es una ampliación –mediante un cierto factor- del otro. En consecuencia, el triángulo AHE es proporcional al triángulo DEF, luego también lo es un triángulo rectángulo con lados proporcionales a 3:4:5. Pero calculemos cual es esa proporción.

Por la proporcionalidad, tenemos que:

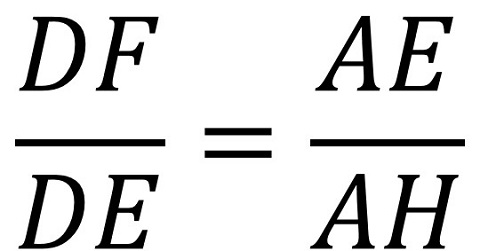
Como conocemos tres de las longitudes AE = 1/2 = DE y DF = 3/8, se obtiene la cuarta, AH = 2/3. Por lo tanto, BH = 1/3 y el punto H nos marca la trisección del lado BA (obteniendo así, de paso, una manera mediante plegado de dividir un segmento –en este caso BA– en tres partes iguales, ya que BH = 1/3 y si M es el punto medio de HA, entonces HM = MA = 1/3).

De nuevo, por la proporcionalidad de los lados de los triángulos AHE y DEF se obtiene que:

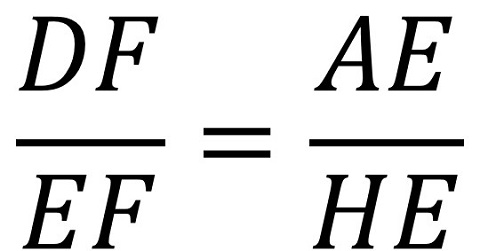
Conocemos tres de las longitudes, DF = 3/8, EF = 5/8 y AE = 1/2, luego se puede calcular la otra, HE = 5/6. Por lo tanto, las medidas del triángulo AHE, si el cuadrado original tiene lado 1, son 1/2, 2/3 y 5/6, proporcional al triángulo 3:4:5 multiplicando por 6. Más aún, el punto H nos da la sexta parte del segmento IE, ya que HI = 1 – 5/6 = 1/6.

Resultado 2 (teorema de Haga):

a) el triángulo rectángulo AHE es proporcional a un triángulo pitagórico 3:4:5;

b) el punto H es un punto de trisección del lado BA, BH = 1/3;

c) el punto H es un punto de “hexasección” del lado IE, HI = 1/6.

Finalmente, utilizando argumentos similares, es decir, la proporcionalidad de los triángulos semejantes y el teorema de Pitágoras, podemos obtener las medidas del tercer triángulo rectángulo IGH. En concreto, HI = 1/6, IG = 1/8 y GH = 5/24, que también es proporcional al triángulo 3:4:5, multiplicando por 24. Más aún, como GB = IG = 1/8, el punto G nos da la octava parte del segmento BA.

Resultado 3 (teorema de Haga):

a) el triángulo rectángulo IGH es proporcional a un triángulo pitagórico 3:4:5;

b) el punto G es un punto de “octosección” del lado BA, BG = 1/8.

Incluso, utilizando el teorema de Pitágoras podemos obtener la longitud del segmento GF, que es la hipotenusa del triángulo JFG (véase la imagen anterior), cuyo cálculo os dejo para vosotros.

En resumen, si consideramos una hoja de papel cuadrada de longitud 1, las medidas obtenidas tras el pliegue aparecen en la siguiente imagen.

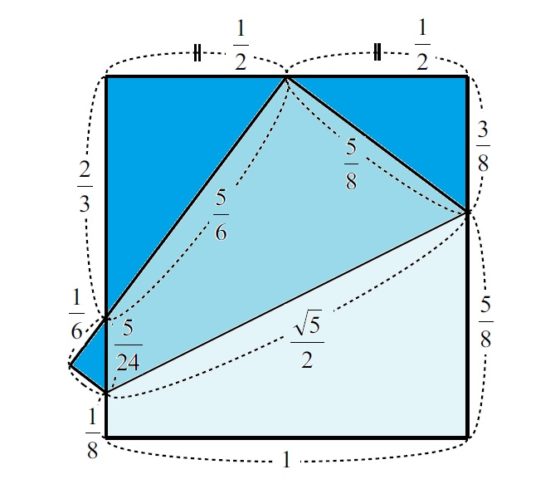
Como hemos visto a lo largo de esta entrada, el primer teorema de Haga nos dice que mediante el plegado “del vértice al punto medio de uno de los lados contrarios” se obtienen tres triángulos rectángulos proporcionales al triángulo egipcio 3:4:5 cuyas medidas son a) 3/8, 1/2 y 5/8; b) 1/2, 2/3 y 5/6; c) 1/8, 1/6 y 5/24, de la longitud del cuadrado original. Por lo tanto, si tomamos una hoja de papel cuadrada de longitud 24 se obtienen tres triángulos pitagóricos de tamaño (9, 12, 15), (12, 16, 20) y (3, 4, 5), como aparece en la imagen.

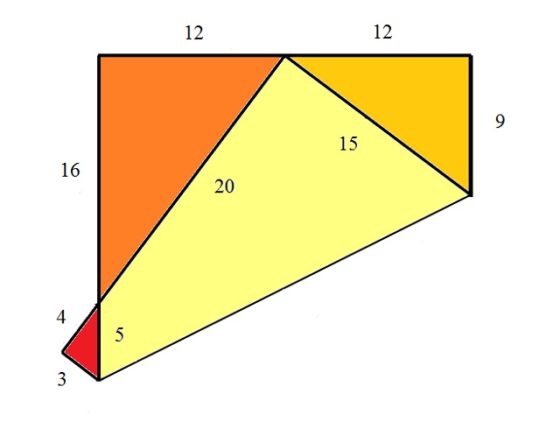
Más aún, podemos observar que también es cierta la siguiente igualdad:

Resultado 4 (teorema de Haga): La suma de los perímetros de los triángulos DEF y IGH es igual al perímetro del triángulo AHE.

Este resultado, el primer teorema de Haga, a caballo entre el origami y la geometría euclídea, fue descubierto por Kazuo Haga en 1978, cuando trabajaba como biólogo especializado en morfología de artrópodos y utilizaba el origami como método para relajarse. Un año más tarde el físico japonés Koji Fushimi publicó en una revista japonesa el resultado de Haga etiquetándolo por vez primera como el “teorema de Haga”.

Bibliografía

1. Pedro Miguel González Urbaneja, Pitágoras, el filósofo del número, Nivola, 2001.

2. Kazuo Haga, Origamics, Mathematical Explorations through Paper Folding, World Scientific, 2008.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica