El mundo está lleno de casualidades. Mi anterior entrada del Cuaderno de Cultura Científica titulada Paseando entre árboles de Pitágoras terminaba con una construcción similar al árbol de Pitágoras, pero tomando como base un triángulo equilátero, en lugar de un triángulo rectángulo, junto a los tres cuadrados apoyados en los lados del triángulo. Esta construcción da lugar, no a un árbol fractal, sino al mosaico rhombitrihexagonal.
Las dos siguientes imágenes son las que cerraban la anterior entrada. La primera es la estructura generada utilizando el triángulo equilátero y los tres cuadrados laterales, después de cuatro pasos, aunque representando solo los cuadrados.
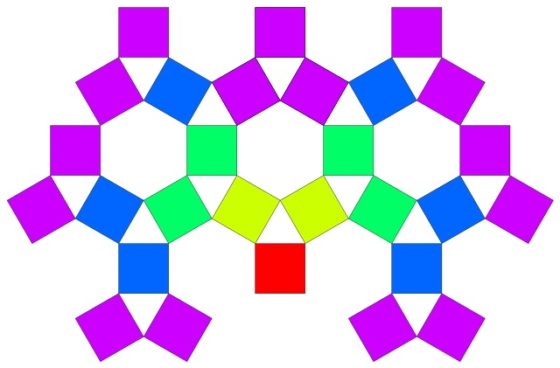
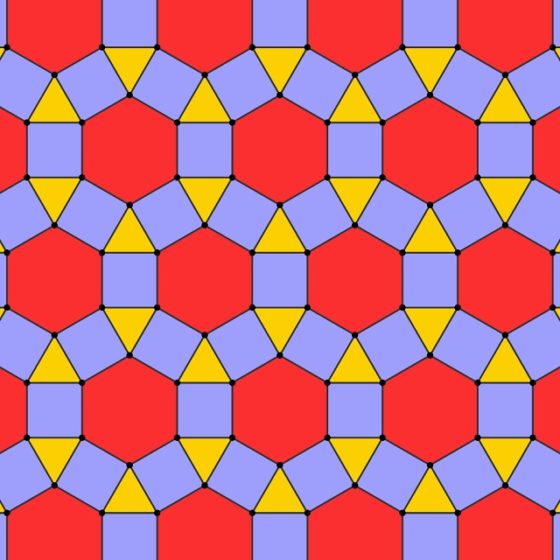
Mientras que la segunda es el mosaico rhombitrihexagonal que, como comentábamos, se puede generar con esta construcción.
Lo curioso es que unos días después de publicarse esa entrada me fui de viaje a Roma, esa monumental y hermosa ciudad italiana que muchos hemos conocido a través del cine, de la mano de Gregory Peck y Audrey Hepburn subidos a una moto Vespa en la película Vacaciones en Roma (1953) de William Wyler o junto a Anita Ekberg y Marcelo Mastroianni en la Dolce Vita (1960) de Federico Fellini, con la mítica escena de sus personajes bañándose en la Fontana de Trevi, entre otras películas.
Mi primera sorpresa llegó nada más aterrizar en el Aeropuerto de Roma-Fuimicino, mientras salía del mismo. Uno de los carteles publicitarios del aeropuerto mostraba la siguiente imagen.


Esta imagen, que pertenecía a la publicidad del pabellón italiano en la Expo Dubai 2020, que debido al covid 19 se está celebrando entre octubre de 2021 y marzo de 2022, no era otra que la de la construcción geométrica anterior. ¡Qué bonita casualidad!
La siguiente casualidad no lo era tanto si tenemos en cuenta que la ciudad de Roma está llena de hermosos mosaicos geométricos muy bien conservados. Con la intención de visitar la Boca de la Verdad, para emular a Gregory Peck y Audrey Hepburn, entré en la Basílica de Santa María en Cosmedin. Allí se encuentra esta antigua máscara de mármol pavonazzetto, que según cuenta la leyenda quién miente se queda sin mano al meterla en el hueco de la boca de la misma. La Basílica de Santa María en Cosmedin fue construida en el siglo VIII sobre los restos romanos del Templum Herculis Pompeiani, templo de la Antigua Roma dedicado a Hércules, y destaca por su decoración en estilo cosmatesco. Este estilo de decoración debe su nombre a la familia Cosmati, una familia de artesanos, de alrededor del siglo XII, que cogían mármol de antiguas ruinas romanas y utilizaban sus fragmentos para crear nuevas decoraciones geométricas, como las que podemos ver en la Basílica de Santa María en Cosmedin.

Observando este hermoso pavimento me llevé algunas sorpresas. Una de ellas fue una parte del pavimento en el que aparecía el mosaico rhombitrihexagonal anteriormente mencionado, que está formado por triángulos equiláteros (aunque en este mosaico cosmatesco estos están divididos a su vez en cuatro pequeños triángulos equiláteros), cuadrados y hexágonos regulares, con mármoles blancos veteados, rojos y verdes. ¡Qué bella realización del mosaico rhombitrihexagonal!

Llegados a este punto podríamos pensar un poco en los mosaicos desde el punto de vista de las matemáticas, de la geometría.
Para empezar, imaginemos que queremos embaldosar un suelo con baldosas que tengan la misma forma y tamaño. En concreto queremos que las baldosas sean sencillas, que sean polígonos regulares, que son aquellos polígonos cuyos lados –y también ángulos interiores- son iguales entre sí, como en el triángulo rectángulo, el cuadrado o polígonos con más lados como el pentágono, el hexágono, el heptágono o el octógono regulares. Además, queremos embaldosar el suelo de forma regular, es decir, no solo que las baldosas sean polígonos regulares, sino que estén pegadas lado con lado. Si pensamos en mosaicos de este tipo, llamados embaldosados o teselaciones regulares, se nos ocurrirán tres sencillos ejemplos que están muy presentes en nuestro día a día, con triángulos equiláteros, con cuadrados y con hexágonos, como se muestra en la siguiente imagen.

El siguiente mosaico del pavimento de la Basílica de Santa María en Cosmedin toma como base el embaldosado regular con cuadrados, aunque algunos cuadrados no son lisos, sino que tienen su propio diseño geométrico (con pequeños cuadrados y triángulos).

Mientras que este otro mosaico del mismo lugar, toma como base el mosaico regular hexagonal. Aunque en este ejemplo los propios lados de los hexágonos están muy marcados al ser pequeñas baldosas –es lo que se llama un teselado hexagonal achaflanado- y además el interior de los hexágonos está a su vez decorado a base de rombos.

Pero volviendo a la geometría, la cuestión importante es si hay más embaldosados regulares. Ya en la entrada Diseños geométricos con chocolate abordábamos esta cuestión, que recuperamos en esta entrada.
Si nos fijamos en un vértice cualquiera de alguno de los tres embaldosados anteriores, formados por triángulos equiláteros, cuadrados o hexágonos regulares, en él confluyen un cierto número de baldosas (triangulares, cuadradas o hexagonales). En el caso del mosaico triangular, en cada vértice se juntan 6 triángulos equiláteros, puesto que el ángulo interior del triángulo equilátero es de 60 grados, y seis veces 60 grados son 360 grados (6 x 60 = 360), que es la vuelta completa alrededor del vértice. En la teselación por cuadrados se juntan 4 de estos polígonos, cada uno de ellos con un ángulo interior de 90 grados en el vértice, y de nuevo, 4 veces 90 grados son 360 grados (4 x 90 = 360). Finalmente, los ángulos interiores de los hexágonos son de 120 grados, lo cual es coherente con el hecho de que alrededor de cada vértice del embaldosado por hexágonos, hay exactamente tres hexágonos en la configuración alrededor del vértice (es decir, 120 x 3 = 360).
La pregunta, llegados a este momento, es si es posible que existan más embaldosados mediante polígonos regulares. La respuesta viene de la mano de la configuración alrededor de cualquier vértice del mosaico. Dada una teselación, alrededor de cada vértice hay un cierto número n de baldosas, luego los ángulos del polígono medirán 360 / n grados, por lo que podemos ver qué posibilidades existen: i) 360 / 2 = 180 grados (que no nos da ningún polígono); ii) 360 / 3 = 120 grados (hexágonos); iii) 360 / 4 = 90 grados (cuadrados); iv) 360 / 5 = 72 grados (pero no hay ningún polígono regular con un ángulo interior de 72 grados); v) 360 / 6 = 60 grados (triángulos); y no hay más posibilidades que nos den un polígono. En consecuencia, acabamos de demostrar el siguiente teorema:
Los únicos embaldosados regulares lado a lado son los formados con triángulos equiláteros, con cuadrados o con hexágonos regulares.
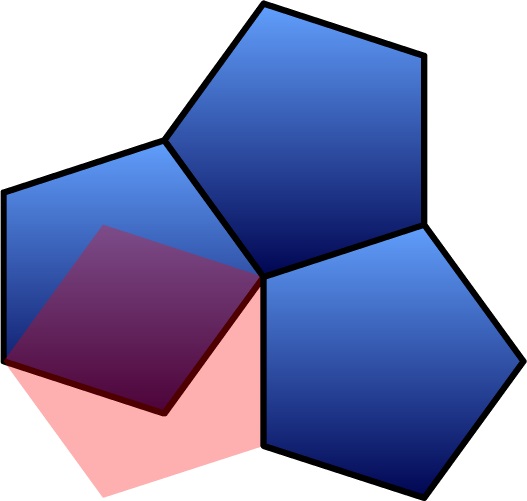
Por cierto, que los ángulos interiores de un pentágono miden 108 grados, de un heptágono 128,6 grados, y en general, para un polígono regular de n lados, no es difícil de probar que el ángulo interior vale (n – 2) x 180 / n grados.
Este tipo de embaldosado regular –con triángulos equiláteros, cuadrados o hexágonos regulares- es muy frecuente en la decoración de nuestra vida. Sin embargo, consideremos embaldosados un poco más complejos. Imaginemos que ahora en lugar de considerar únicamente baldosas con la forma de un único polígono regular, se construyen mosaicos utilizando varios polígonos regulares distintos como baldosas. El número de lados de las baldosas puede variar, pero no la longitud de cada lado, ya que las baldosas se seguirán pegando lado con lado. Por ejemplo, en el mosaico rhombitrihexagonal se utilizan baldosas triangulares, cuadradas y hexagonales, con lados de la misma longitud. Otro ejemplo aparece en la siguiente imagen, que es un mosaico formado por hexágonos y triángulos equiláteros cuyos lados son iguales (aunque de nuevo, en este pavimento, los triángulos equiláteros están divididos a su vez en cuatro pequeños triángulos equiláteros, para darle más riqueza geométrica al pavimento), que se llama mosaico trihexagonal.

Estos dos ejemplos de mosaicos se llaman embaldosados o teselaciones uniformes, o semiregulares, ya que alrededor de cualquiera de sus vértices se tiene la misma configuración de polígonos regulares, en el primer caso en cada vértice vemos cuadrado, triángulo, cuadrado y hexágono, mientras que en el segundo es triángulo, hexágono, triángulo, hexágono. Si queremos estudiar qué tipos de teselaciones uniformes existen, el procedimiento es similar al anterior para las regulares.
Para empezar, el número de polígonos regulares –denotémoslo k– alrededor de cada vértice del embaldosado semiregular es menor o igual que 6, ya que el polígono regular con menor ángulo interior es el triángulo, con un ángulo de 60 grados, y solo puede haber 6 triángulos en un vértice. Por lo tanto, tomando los posibles valores de k como 3, 4, 5 o 6, y realizando un pequeño razonamiento sobre los ángulos interiores de los polígonos regulares se puede deducir que las únicas posibilidades son las siguientes:
i) Para k = 6 (seis polígonos en cada vértice), solo puede haber 6 triángulos equiláteros alrededor de cada vértice. A esta configuración la denotamos (3, 3, 3, 3, 3, 3) y da lugar a la teselación regular triangular.
ii) Para k = 5 (cinco polígonos en cada vértice), hay tres configuraciones posibles (3, 3, 3, 3, 6) –cuatro triángulos y un hexágono-, (3, 3, 3, 4, 4) –tres triángulos y dos cuadrados- y (3, 3, 4, 3, 4) –de nuevo, tres triángulos y dos cuadrados, pero en otro orden-.
iii) Para k = 4, hay siete configuraciones posibles, a saber (3, 3, 6, 6) –dos triángulos y dos hexágonos-, (3, 6, 3, 6) –dos triángulos y dos hexágonos, con otro orden-, (3, 4, 4, 6) –un triángulo, dos cuadrados y un hexágono-, (3, 4, 6, 4) –un triángulo, dos cuadrados y un hexágono, con otro orden-, (3, 3, 4, 12) –dos triángulos, un cuadrado y un dodecágono-, (3, 4, 3, 12) –dos triángulos, un cuadrado y un dodecágono, en otro orden- y (4, 4, 4, 4) –cuatro cuadrados-.
iv) Y para k = 3, hay diez configuraciones posibles, que son (3, 7, 42), (3, 8, 24), (3, 9, 18), (3, 10, 15), (3, 12, 12), (4, 5, 20), (4, 6, 12), (4, 8, 8), (5, 5, 10) y (6, 6, 6).
En la siguiente imagen vemos todas las 21 posibles configuraciones en los vértices de una teselación uniforme.
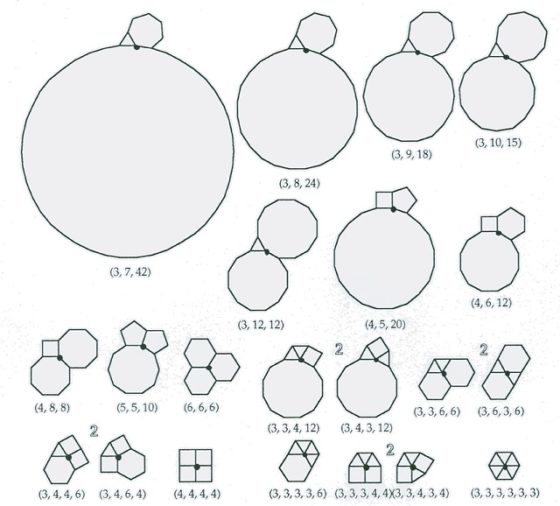
Por lo tanto, no puede haber embaldosados uniformes tal que los vértices tengan configuraciones diferentes a estas 21 que acabamos de mostrar. Sin embargo, esto no quiere decir que todas estas configuraciones den lugar a mosaicos semiregulares. De hecho, trabajando configuración a configuración se puede obtener que solamente existen 8 embaldosados uniformes, obviando los 3 regulares ya conocidos (luego 11 en total), que se muestran en la siguiente imagen.
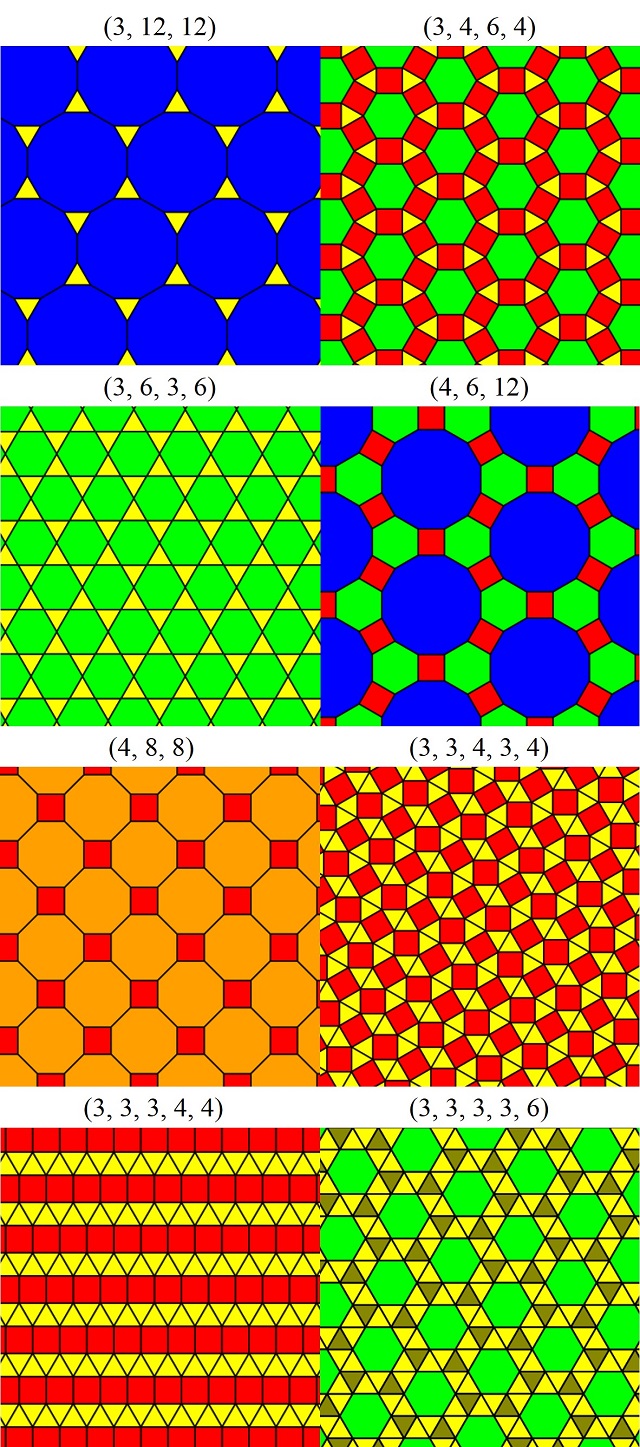
Por ejemplo, si se hacen “baldosas” de cartón (o de cualquier otro material) de triángulos equiláteros (3) y hexágonos (6) se puede ver que la configuración (3, 3, 6, 6) no da lugar a ningún embaldosado, aunque la configuración (3, 6, 3, 6) sí, como se muestra en la anterior imagen. Veamos el razonamiento. Dada la configuración (3, 3, 6, 6) en un vértice (como se muestra en la siguiente imagen, en gris las dos baldosas hexagonales y en azul las dos triangulares) e intentamos completar el vértice marcado en amarillo con un hexágono solo hay dos opciones. En la primera (imagen superior) en el vértice amarillo quedaría la configuración (3, 6, 3, 6), que no es la buscada, mientras que en la segunda (imagen inferior) nos provocaría que en el vértice marcado en rosa aparecieran ya tres triángulos, lo que tampoco es la configuración buscada (3, 3, 6, 6). Luego esta configuración es imposible.
Volviendo a la Basílica de Santa María en Cosmedin, los dos mosaicos mostrados arriba se corresponden con las configuraciones (3, 4, 6, 4), el rhombitrihexagonal, y (3, 6, 3, 6), el trihexagonal. Pero veamos que aún hay algún otro embaldosado uniforme en esta hermosa iglesia. En la siguiente imagen podemos apreciar el mosaico (3, 6, 3, 6) anteriormente comentado y el (4, 8, 8), llamado embaldosado cuadrado truncado, formado por cuadrados y octógonos.

Si a la teselación (3, 3, 3, 3, 6), que se conoce con el nombre de teselado hexagonal romo, se le juntan los dos triángulos de cada vértice del hexágono para formar un rombo, como se muestra en esta imagen
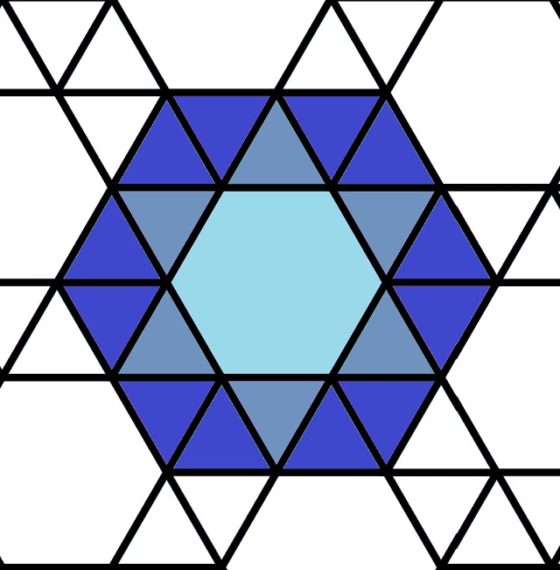
se obtiene el siguiente pavimento de esta basílica romana.

Llegados a este punto de la escritura de esta entrada, me puse a buscar algún ejemplo más de pavimento cosmatesco con alguno de los mosaicos uniformes que me faltaban, entonces me encontré con esta imagen (aunque como la descarté en un inicio no tengo la referencia de la misma, ¡perdón!).

En la misma teníamos triángulos, cuadrados y octógonos, luego no podía ser uno de los once embaldosados uniformes. Entonces me fijé en los vértices y observé que había dos tipos de vértices, aquellos con una configuración (3, 8, 3, 8) y otros con (3, 4, 3, 8). Como el ángulo interior de un octógono es de 135 grados, en la primera configuración los ángulos alrededor del vértice sumarían 60 + 135 + 60 + 135 = 390 grados, lo cual supera la vuelta entera, mientras que en el otro caso, la suma de los ángulos alrededor del vértice sería 60 + 90 + 60 + 135 = 345, que no llega a una vuelta entera. Por lo tanto, en este mosaico hay una pequeña trampa y las baldosas no son polígonos regulares, por ejemplo, el triángulo puede no ser equilátero o el cuadrado ser realmente cualquier otro cuadrilátero, ya sea un paralelogramo, un trapecio o un trapezoide.
Aunque podíamos haber tenido un mosaico con polígonos regulares y dos tipos de vértices con configuraciones distintas, es lo que se llama teselaciones 2-uniformes. Por ejemplo, en la siguiente imagen podemos ver un mosaico de la Catedral de Santa María de la Asunción en Sutri.

Si nos fijamos bien en la parte posterior de la imagen y consideramos el rombo formado por dos triángulos equiláteros, entonces la estructura del mosaico sería la siguiente.

Es un mosaico que tiene dos tipos de vértices, con configuraciones (3, 3, 6, 6) y (3, 6, 3, 6), es decir, es un embaldosado 2-uniforme. Pero dejemos este tipo de embaldosados para otra ocasión.
Aunque como decía al principio de esta entrada del Cuaderno de Cultura Científica, la Basílica de Santa María en Cosmedin me deparó alguna sorpresa más, pero de eso hablaremos en una siguiente entrada.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

¿Conocían los romanos el triángulo fractal de Sierpinski? — Cuaderno de Cultura Científica
[…] escribí en mi anterior entrada del Cuaderno de Cultura Científica, titulada Geometría en los pavimentos romanos cosmatescos, observando el hermoso pavimento de la Basílica de Santa María en Cosmedin en Roma, en la cual se […]
Los embaldosados de Truchet y el puzle del diamante — Cuaderno de Cultura Científica
[…] es un interesante tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. En la entrada de hoy del Cuaderno de Cultura Científica vamos a centrarnos en los patrones de […]