En esta entrada del Cuaderno de Cultura Científica vamos a hablar de una bella construcción geométrica relacionada con el teorema de Pitágoras, el conocido como árbol (fractal) de Pitágoras.

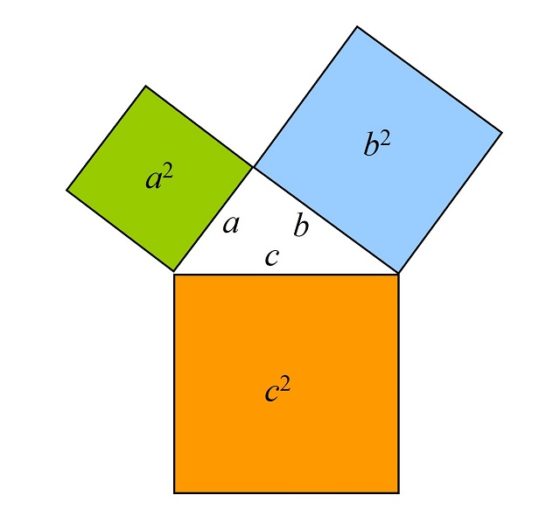
Esta construcción geométrica surge del diagrama básico asociado al teorema de Pitágoras. Recordemos que este resultado geométrico digno de una hecatombe (véase Pitágoras sin palabras) dice que “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” o en su versión más algebraica, que a² + b² = c², si a y b son los catetos y c la hipotenusa del triángulo rectángulo. El esquema básico asociado es el siguiente.

El árbol de Pitágoras es un fractal (véase Fractus, arte y matemáticas) que fue inventado por el ingeniero y profesor de matemáticas neerlandés Albert E. Bosman en 1942 (aunque en esos momentos Bosman desconocía que esa estructura fuese un fractal). Esta construcción fue publicada, por primera vez, en su libro Het wondere onderzoekingsveld der vlakke meetkunde (algo así como El maravilloso campo de exploración de la geometría plana) de 1957.

Para explicar la construcción de este objeto fractal vamos a empezar por un caso particular, el mismo que utilizó Bosman, que es el esquema pitagórico para un triángulo rectángulo isósceles, es decir, los catetos son de la misma longitud (lo que nos lleva a que los ángulos del triángulo son 45, 45 y 90 grados), que se ve en la siguiente imagen.

La construcción del árbol de Pitágoras, para un triángulo rectángulo isósceles, es la siguiente. En el primer paso se tiene el esquema básico del teorema de Pitágoras, es decir, un cuadrado abajo, cuyo lado es la hipotenusa del triángulo rectángulo isósceles, y dos cuadrados iguales arriba, cuyos lados son los catetos del triángulo (véase la anterior imagen). Obsérvese que, por el teorema de Pitágoras, el área del cuadrado de abajo es igual a la suma de las áreas de los dos cuadrados de arriba.

Para el segundo paso, se considera cada uno de los dos cuadrados de la parte superior (el de la izquierda y el de la derecha) y se actúa sobre ellos como en el primer paso, es decir, añadiendo dos nuevos cuadrados para cada uno de ellos que con el anterior conforman un nuevo esquema básico del teorema de Pitágoras. El resultado de este segundo paso es el siguiente:

De nuevo, por el teorema de Pitágoras la suma de las áreas de los cuatro nuevos cuadrados es igual a la suma de las áreas de los dos cuadrados intermedios, que es igual al área del cuadrado de la base.

En el paso tercero se realiza la misma operación, pero para cada uno de los cuatro nuevos cuadrados, incorporándose así a la construcción ocho nuevos cuadrados, como aparece en la siguiente imagen.

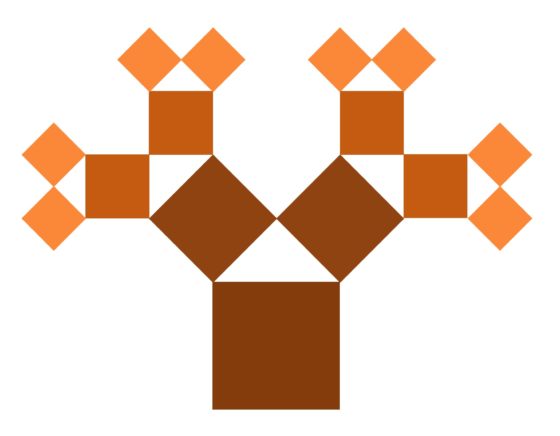
Y así se continúa en cada paso, siempre añadiendo un par de nuevos cuadrados asociados a cada uno de los cuadrados “externos” del paso anterior. Además, la suma de las áreas de los cuadrados añadidos en cada paso es igual al área del cuadrado base.

El fractal conocido como árbol de Pitágoras se genera cuando llevamos esta construcción hasta su límite infinito. El resultado es el que aparece en la siguiente imagen (que hemos generado mediante el Pythagorean tree generator).

En la siguiente imagen podemos disfrutar del dibujo que realizó el profesor de matemáticas Alfred E. Bosman, por cierto, vecino del artista M. C. Escher (1898-1972), de su construcción.

Volviendo a la construcción del árbol de Pitágoras, la cantidad de cuadrados en cada paso es 1 (si tomamos como paso cero cuando tenemos solo el cuadrado inicial de la hipotenusa), 2, 4, 8, 16, 32, etc., es decir, 2ⁿ para el paso n-ésimo. Más aún, si el cuadrado inicial –situado abajo- tiene lado 1, luego área también 1, entonces el área –por el teorema de Pitágoras- de los cuadrados añadidos en cada paso son 1/2, 1/4, 1/8, etc., es decir, el área de cada uno de los cuadrados del paso n-ésimo es 1 / 2ⁿ.

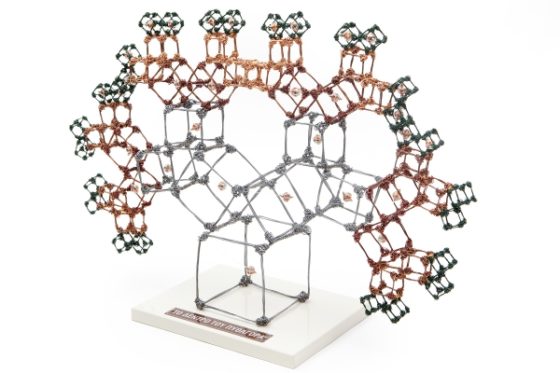
Esta construcción, el árbol de Pitágoras, ha inspirado a algunos artistas. Uno de ellos, el autor de la escultura con la que iniciábamos esta entrada del Cuaderno de Cultura Científica, el matemático, científico computacional y artista neerlandés Koos Verhoeff (1927-2018), del cual vemos otra escultura.

El escultor neerlandés Anton Bakker, dentro de su proyecto artístico Perspectives in Symmetry incluye una serie de esculturas en homenaje a su mentor, el artista y matemático Koos Verhoeff.

El artista belga Jos de Mey (1928-2007), conocido por sus pinturas y dibujos de objetos imposibles, también utilizó el árbol de Pitágoras dentro de sus composiciones. A continuación, mostramos algunos ejemplos.

Por otra parte, en la entrada Pitágoras en el arte mostrábamos una escultura del artista conceptual austriaco Hartmut Skerbisch (1945-2009) basada en el árbol fractal de Pitágoras. Sin embargo, vamos a añadir en esta entrada la escultura de otra artista para terminar esta parte. Se trata de la obra Recogiendo frutos del árbol de Pitágoras (2018), de la profesora de matemáticas y artista griega Georgia J. Maragkou.

Pero sigamos con la construcción del árbol de Pitágoras. De la misma forma que lo hemos construido este fractal a partir del diagrama básico del teorema de Pitágoras para el triángulo rectángulo isósceles, se puede hacer para cualquier otro triángulo rectángulo, como así aparece también en el libro de Bosman. Aunque ahora la construcción, aunque igualmente hermosa, ya no será igual de simétrica que lo era para el caso isósceles. Por ejemplo, en la siguiente imagen vemos el resultado de esta construcción geométrica para el triángulo rectángulo de ángulos 30, 60 y 90 grados, realizada también con el generador del árbol de Pitágoras: Pythagorean tree generator.

La parte principal de este árbol de Pitágoras está relacionada con la serie de obras del artista conceptual estadounidense Mel Bochner (1940) tituladas Pitágoras.

El artista suizo Eugen Jost (1950), cuya obra artística podríamos catalogar como matemática, tiene una serie de cuadros titulados Pitágoras encuentra a Fibonacci, basada en esta construcción, en la rama principal de la misma. Pitágoras aparece a través de la construcción de la rama del árbol de Pitágoras, mientras Fibonacci aparece a través de la conocida sucesión de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, … (véase Póngame media docena de fibonaccis), ya que las áreas de los cuadrados, desde los pequeños a los mayores, son los primeros elementos de esta sucesión.

El árbol de Pitágoras, para el caso general, también ha sido utilizado por el matemático y artista japonés Kentaro Okamoto. En este caso utiliza un triángulo rectángulo de ángulos, más o menos, de 52, 38 y 90 grados, además el área de cada color es la misma, como hemos explicado en la construcción (debido al teorema de Pitágoras).

El propio Bosman también observó (como puede verse en su libro) que en su construcción del árbol de Pitágoras que si se cambia alternativamente la orientación del triángulo rectángulo (no para el caso del triángulo isósceles que se queda igual) entonces se obtiene un nuevo tipo de árbol de tipo conífera. Por ejemplo, si se toma el triángulo rectángulo de ángulos 30, 60 y 90 grados, cuyo árbol de Pitágoras se ha representado arriba, entonces el árbol de Pitágoras de tipo conífera quedaría de la siguiente forma (realizado, de nuevo, con el Pythagorean tree generator).

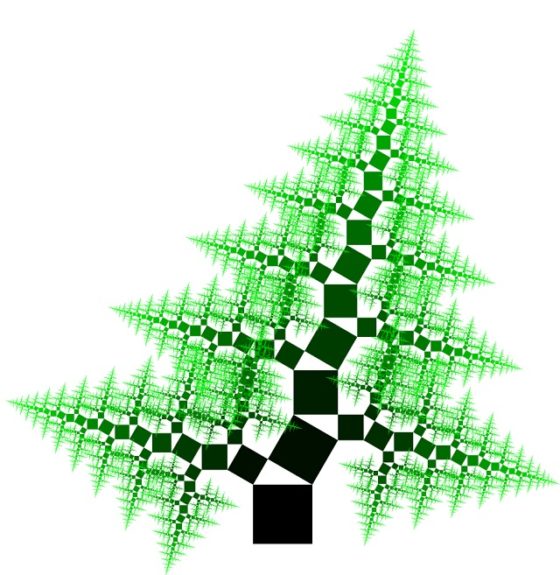
O se puede generar un árbol de tipo semiconífera, como el de la siguiente imagen.

A partir de estas simples, pero hermosas, ideas de Alfred E. Bosman se pueden generar estructuras arbóreas diferentes. Por ejemplo, cambiar los cuadrados originales por rectángulos, de forma que se obtienen imágenes como las siguientes (que son de tipo normal, semiconífera y conífera), generadas con el Pythagoras tree generator de la página online math tools:

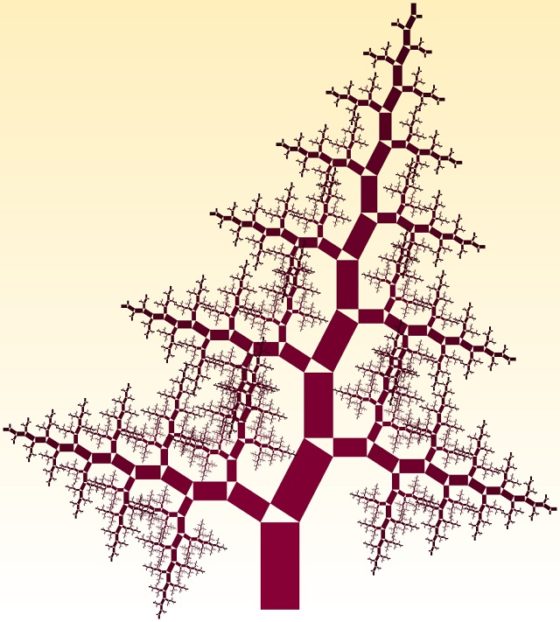
Más aún, podemos cambiar en cada paso los ángulos de los triángulos rectángulos y las dimensiones de los rectángulos, obteniendo imágenes como la siguiente (generadas con el Pythagoras tree generator).

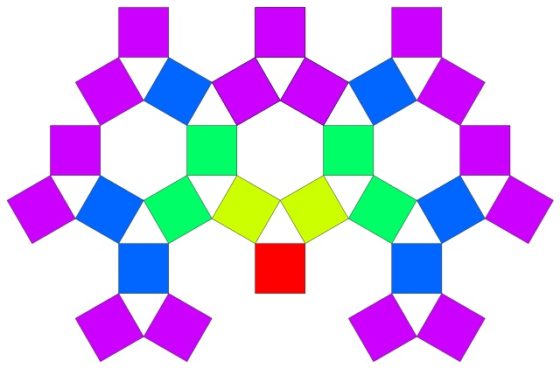
Otro elemento que se puede modificar es el triángulo rectángulo. Es decir, tomar un triángulo cualquiera y colocar tres cuadrados en sus lados, creando así el diagrama básico, como en el caso del teorema de Pitágoras. Por ejemplo, si se toma un triángulo equilátero (de lados iguales y ángulos iguales, de 60 grados), se generaría la siguiente estructura, después de cuatro pasos (imagen de wikimedia commons).

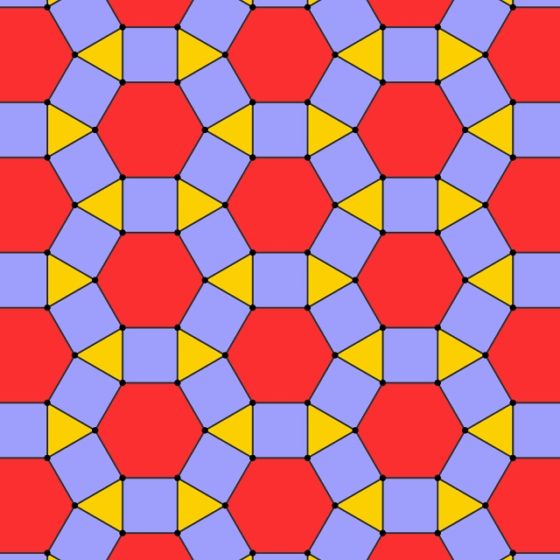
De hecho, de esta forma se genera el mosaico Rhombitrihexagonal, que vemos en la siguiente imagen (Wikimedia Commons).

Podríamos hablar de más posibles variaciones, pero ya son demasiadas variaciones para una sola entrada, por lo que lo dejaremos aquí. Aunque, vamos a terminar con una artista matemática estadounidense, Gwen Beads, que utiliza el árbol de Pitágoras en algunas de sus obras, como en Doodle 35: conversación en la azotea (2019).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica