La banda de Moebius es un sorprendente objeto topológico, una superficie con una sola cara y un solo borde, con propiedades muy curiosas (véanse el video La banda de Moebius de la sección Una de Mates del programa de televisión Orbita Laika; el libro La banda de Moebius, de Clifford Pickover; el libro Festival mágico-matemático de Martin Gardner; o algunas de las entradas de la sección Matemoción, del Cuaderno de Cultura Científica, que mencionamos en la bibliografía; por citar algunas referencias) que ha cautivado a muchísimas personas, tanto de dentro como de fuera de las matemáticas.

A pesar de que es el objeto topológico por excelencia, en la entrada de hoy vamos a fijarnos en un problema geométrico relacionado con su construcción con una tira de papel.

Para empezar, una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras y dos bordes, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde.

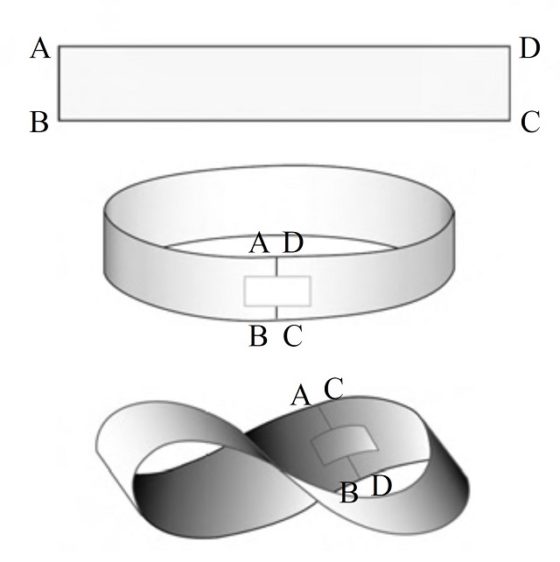
El problema geométrico consiste en construir una banda de Moebius con una tira de papel lo más corta posible. Es decir, dada una tira de papel (como la de la siguiente imagen) que tiene una anchura a y una largura b, se trata de construir una banda de Moebius con una largura b lo más corta posible (dejando fija la anchura a).

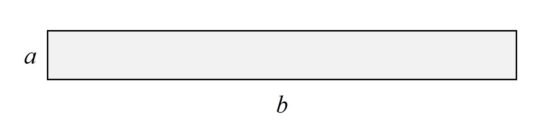
Si la tira de papel es bastante larga, como la de la imagen anterior (podemos construir en casa una tira como la de la imagen que, para una anchura de 10 cm, tendría una largura de 96 cm –o también, para una anchura de 2cm, la largura es de 19,2 cm–), entonces la cinta de Moebius que se construye con ella es bastante holgada, con lo cual podemos recortarla en largura (hacerla más corta) y seguir construyendo nuestra superficie de una sola cara. La cuestión es hasta dónde podríamos ir recortando en la largura.

La banda de Moebius que hemos construido la podemos “aplanar” de la forma en la que aparece en esta imagen, que tiene una forma de tipo triangular (que nos recuerda al símbolo del reciclaje).

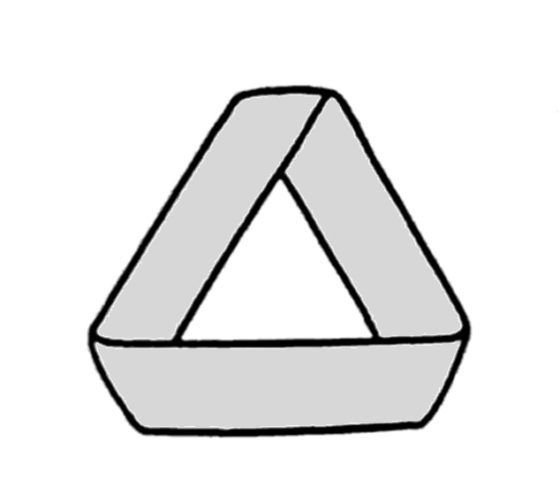
Vemos que efectivamente tiene holgura, hay espacio en el centro. Entonces, si vamos recortando la largura de la banda iremos cerrando ese hueco central, como se muestra en la siguiente imagen, hasta llegar el momento en que se cierre el hueco. Además, como podemos observar, en ese momento final lo que ocurre es que tenemos un hexágono.

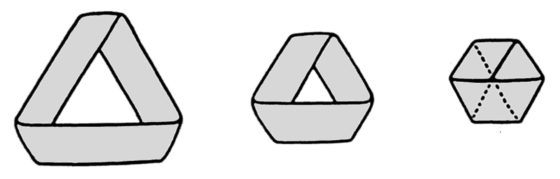
En concreto, nuestra banda de Moebius “recogida” está formada por nueve triángulos equiláteros, como se muestra en la siguiente imagen. Los pares de triángulos equiláteros de papel 2 y 3, 5 y 6, así como 8 y 9, están superpuestos, uno encima del otro, en nuestra banda retorcida, mientras que los triángulos equiláteros 1, 4 y 7 están solos.

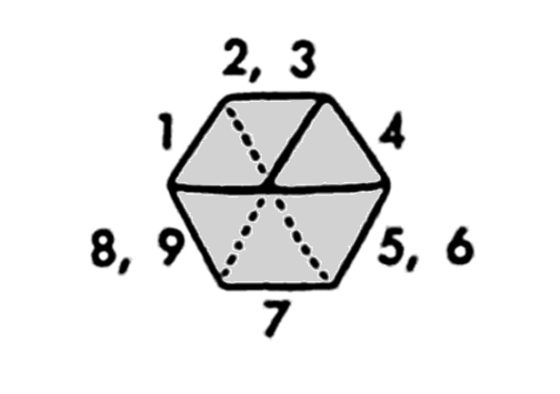
Para conocer cuánto hemos acortado nuestra tira de papel, o más bien, hasta que longitud (respecto de la anchura) hemos acortado, vamos a separar/cortar de nuevo nuestra tira y desplegarla. Tendremos en ella los nueve triángulos equiláteros que, si cortamos en la banda de Moebius justo por el medio de uno de ellos, quedan distribuidos en la tira como se muestra en la imagen.

Para calcular, a partir de la imagen anterior, la relación de la largura (b) respecto a la anchura (a), vamos primero a calcular el lado de cada triángulo equilátero, en función de la anchura a. Para ello vamos a utilizar el teorema de Pitágoras sobre el triángulo rectángulo de la izquierda, que es la mitad del triángulo equilátero. Si llamamos x a la longitud del lado del triángulo equilátero, tendremos el siguiente esquema.

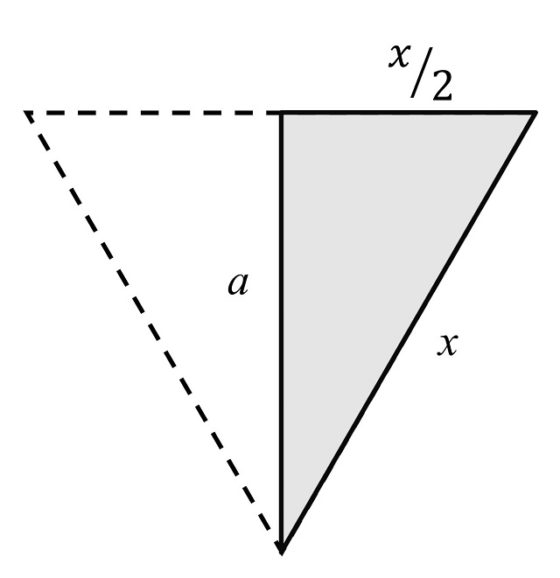
Luego, por el teorema de Pitágoras (la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa):

Y despejando x, en función de a, se obtiene que:

Por lo tanto, si tenemos en cuenta que la tira de papel que hemos obtenido tiene una largura (b) que es 4,5 veces el lado del triángulo equilátero (x), como se puede observar en una de las imágenes anteriores, entonces se tiene que la largura de la tira es igual a:

La largura es aproximadamente 5, 2 veces la anchura (ajustando un poco más, 5,196). Es decir, si nuestra tira de papel tuviese una anchura de 10 centímetros, la largura sería de 51,96 centímetros (recordemos que la inicial tenía una anchura de 10 cm y una largura de 96 cm).

El matemático Stephen Barr, en su interesante libro Experiments in Topology, nos cuenta que es posible reducir la largura de la tira de papel a la tercera parte.

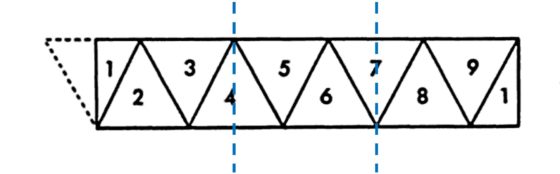
Veamos cómo construir la banda de Moebius a partir de la tercera parte de la banda de nueve triángulos equiláteros. Ahora nos quedamos con un trozo de tira de papel con tres triángulos equiláteros, por ejemplo, los tres de la izquierda de la imagen anterior, dos enteros en el centro y dos mitades en los laterales.

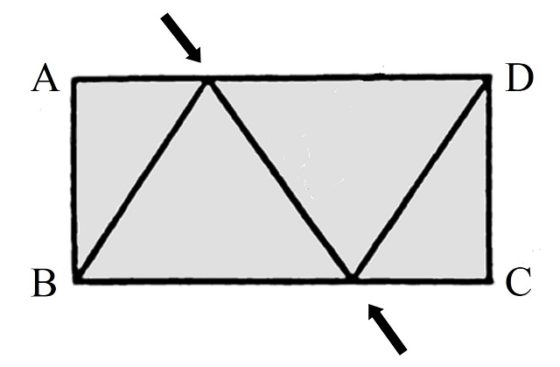
Para construir la banda de Moebius debemos pegar el lateral AB con el lateral opuesto, después de dar media vuelta, es decir, con CD. En particular, el punto A se pega con el punto C y B con D. Para ello, primero doblamos por el lado común de los dos triángulos equiláteros enteros (marcado con las flechas en la imagen), de forma que el triángulo equilátero de la derecha queda sobre el de la izquierda, como se ve en la siguiente imagen.

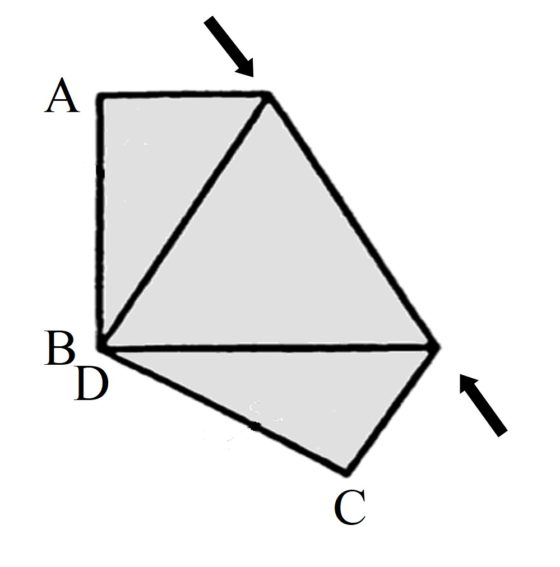
Ahora, doblamos las dos mitades laterales de triángulo equilátero (que son triángulos rectángulos), la que tiene al lado AB y la que tiene al lado CD, colocándolas encima del triángulo equilátero entre ellos (formado por la superposición de los anteriores triángulos equiláteros), como se muestra en la imagen.

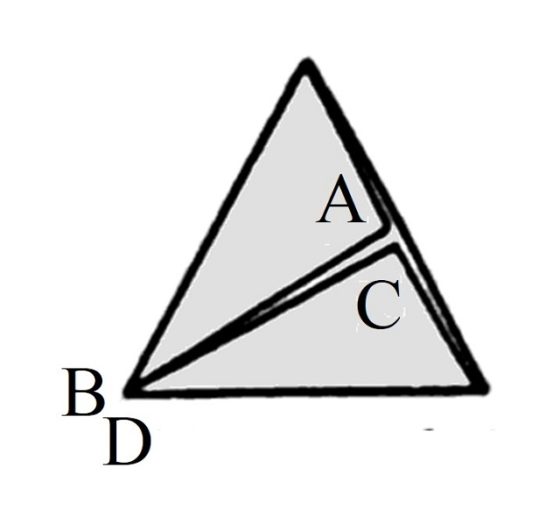
Entonces, se pegan los lados AB y CD obteniéndose una banda de Moebius. A las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica os animo a que realicéis esta construcción en vuestra casa, o donde deseéis claro.

¿Cuánto se ha reducido ahora la largura (respecto de la anchura)? Como habíamos dicho anteriormente, se reduce a la tercera parte de la anterior reducción, es decir, ahora la largura (b) es igual a:

Por ejemplo, nuestra tira original de 10 cm de anchura y 96 cm de largura, la habíamos reducido a una largura de 51,96 cm, que ahora la hemos reducido a 17,32 cm (la raíz de tres es igual a 1,732).

En el libro Experiments in Topology se plantea la cuestión de si se podría realizar una banda de Moebius, con una tira de papel cuadrada. Si consideramos la tira de papel anterior, de 10 cm de anchura, sería una largura de también 10 cm. El propio Stephen Barr nos muestra la solución.

Si partimos de una tira de papel ABCD cuadrada, como la de la imagen, se empieza doblando por una de las diagonales.

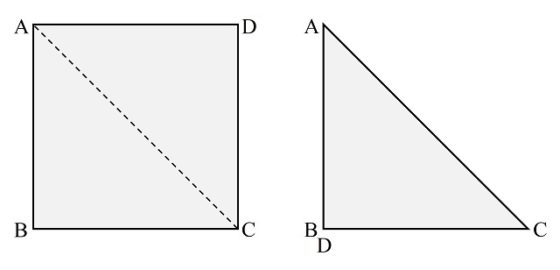
A continuación, se dobla por la otra diagonal, quedando un triángulo (isósceles y rectángulo) que es la cuarta parte del cuadrado original.

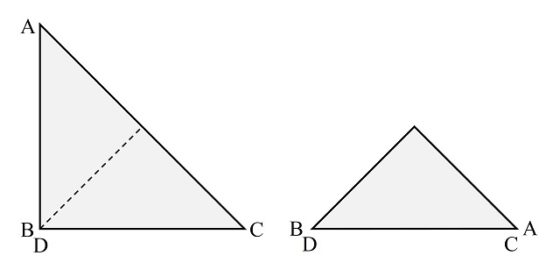
Entonces, se pegan los lados AB con CD para formar la banda de Moebius. Hemos de tener cuidado, ya que los lados a pegar están en la base del triángulo obtenido, pero en distintas capas. El lado AB está en la capa de arriba, mientras que el lado CD está en la tercera capa empezando por arriba (o en la segunda empezando por abajo). Por este motivo, si hacemos esta construcción en nuestra casa, tenemos que tener un poco de cuidado cuando vayamos a poner el celo para pegar esos lados.

A pesar de estos ingeniosos métodos de Stephen Barr para crear bandas de Moebius para tiras de papel que son bastante cortas –el caso del cuadrado es significativo- como para intentar dar medio giro a un lado y pegarlo con el opuesto, el gran divulgador de las matemáticas, el estadounidense Martin Gardner (1914-2010), en una de sus columnas de Juegos matemáticos de la revista Scientific American (recogida en el libro The Sixth Scientific American Book of Mathematical Puzzles and Diversions, publicado por vez primera en 1971), plantea el problema de hacer una banda de Moebius para tiras más cortas aún, por ejemplo, si es el doble de ancha que larga.

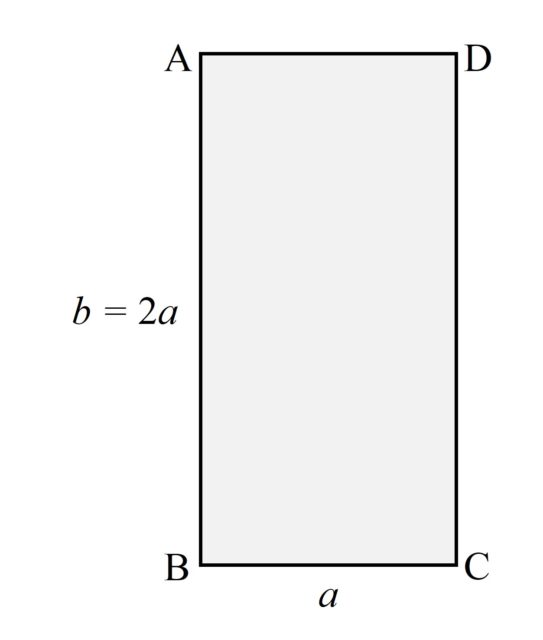
De nuevo, deberíamos de pegar el lado AB con su opuesto, después de girar este media vuelta, es decir, con el lado CD. El problema evidente es que el una tira de papel muy corta, necesitaríamos una mayor largura para poder pegar los lados opuestos –después de girar uno media vuelta-.

La genial idea de Martin Gardner fue conseguir que la anchura “fuese más corta aún”, de manera que con esa nueva anchura la largura nos permita girar la banda media vuelta y pegar los extremos. ¿Cómo conseguir reducir la anchura, sin modificar las dimensiones reales de nuestra tira de papel? La idea es ingeniosa. Se trata de realizar una cantidad de pliegues horizontales –igualmente espaciados- a nuestra tira de papel de forma que se generen una cantidad impar de zonas plegadas iguales.

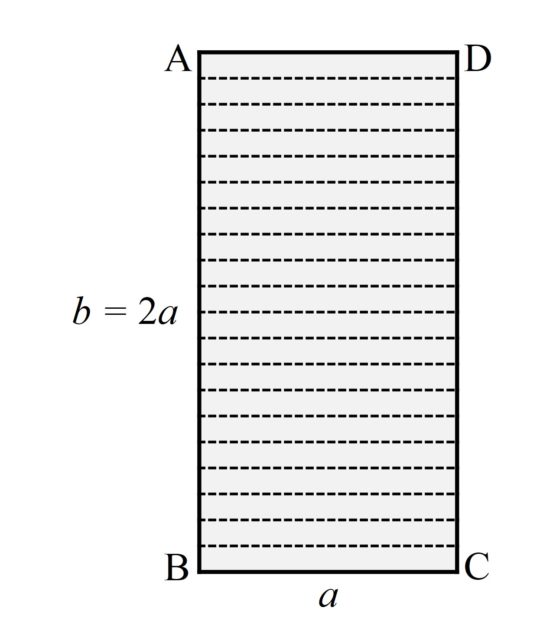
En la anterior imagen hemos realizado 20 pliegues, que generan 21 zonas, que se pliegan en acordeón formando una tira de papel cuya anchura se ha reducido en relación a la largura.

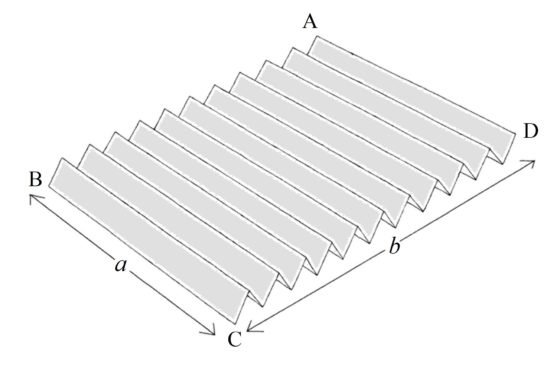
La “nueva” tira, después de realizar completamente estos pliegues, tiene una largura suficiente (aunque recordemos que está formada por 21 capas de papel, que se han generado al realizar los pliegues) como para poder girarla media vuelta y pegar los lados plegados, AB con CD (como se muestra en la siguiente imagen, sacada del libro de Martin Gardner).

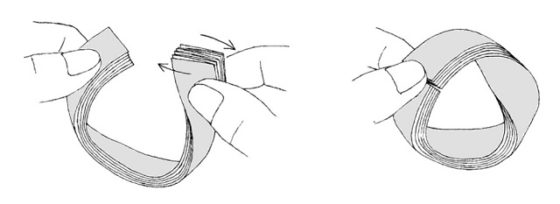
¡Qué maravilla de construcción de bandas de Moebius a partir de tiras de papel muy cortas!

Bibliografía

1.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.

2.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.

3.- Marta Macho, Poesía retorcida sobre la banda de Moebius, Cuaderno de Cultura Científica, 2016.

2.- Marta Macho, Otto Spiegel, de la simetría a la teoría del caos, Cuaderno de Cultura Científica, 2019.

3.- Raúl Ibáñez, De menú para hoy, dos novelas gráficas negras con salsa matemática, Cuaderno de Cultura Científica, 2019.

4.- Raúl Ibáñez, Guía matemática para el cómic ‘Promethea’, Cuaderno de Cultura Científica, 2020.

5.- Raúl Ibáñez, Arte Moebius (I), Cuaderno de Cultura Científica, 2020.

6.- Raúl Ibáñez, Arte Moebius (II), Cuaderno de Cultura Científica, 2020.

7.- Stephen Barr, Experiments in Topology, Dover, 1989.

8.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica