El estudio de los patrones de embaldosado o teselado es un interesante tema con interés tanto en el ámbito de la ciencia y la tecnología, como del arte y el diseño. En la entrada de hoy del Cuaderno de Cultura Científica vamos a centrarnos en los patrones de teselado con un único tipo de baldosa –o tesela-, pero que además es de una gran sencillez, la conocida como “baldosa de Truchet”. Es la baldosa cuadrada dividida por la diagonal en dos zonas triangulares de dos colores distintos, por ejemplo, gris y negro, como la que aparece en la imagen.

En el libro El sentido del orden (1979) del historiador del arte británico de origen austriaco Ernst H. Gombrich (1909-2001), conocido entre otras obras por su famosa Historia del Arte (1950), se reproducen algunos de los diseños de patrones de teselados realizados con esta baldosa que aparecen en el libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal (1722), del padre carmelita francés Dominique Doüat (siglo XVIII).

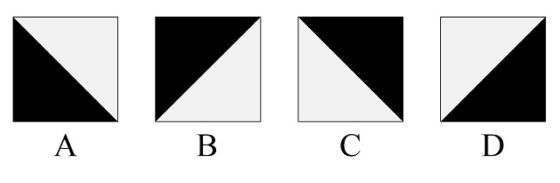
Estos son solamente dos de los setenta y dos diseños de patrones de embaldosados incluidos en el libro de Doüat (véase en la bibliografía un enlace a una edición facsímil con extractos y otro a la obra completa que pueden consultarse), que es un texto en el que se realiza un análisis combinatorio de los embaldosados que pueden generarse con esa baldosa. El padre Doüat empieza nombrado las cuatro orientaciones de la baldosa como A, B, C y D, como se muestra en la imagen.

A partir de ese momento, el carmelita se dedica a realizar un análisis combinatorio con las letras A, B, C y D, empezando por los casos más sencillos, que es la única forma de clasificar con cierto orden, entre las páginas 20 y 189 (en muchas ocasiones son páginas con listados de letras). Por ejemplo, los posibles embaldosados con tan solo dos baldosas (en horizontal) serían dieciséis (cuatro posibilidades para cada posición, cuatro al cuadrado): AA, BB, CC, DD, AB, BA, CA, DA, AC, BC, DC, AD, BD, CD, DC. Al final de la obra se incluyen ilustraciones relacionadas con ese análisis combinatorio. Por ejemplo, en la siguiente ilustración se recogen los cuatro embaldosados de una sola baldosa (que son las cuatro orientaciones posibles) y de dos baldosas (en horizontal), que son las que se corresponden con el listado anterior de dieciséis.

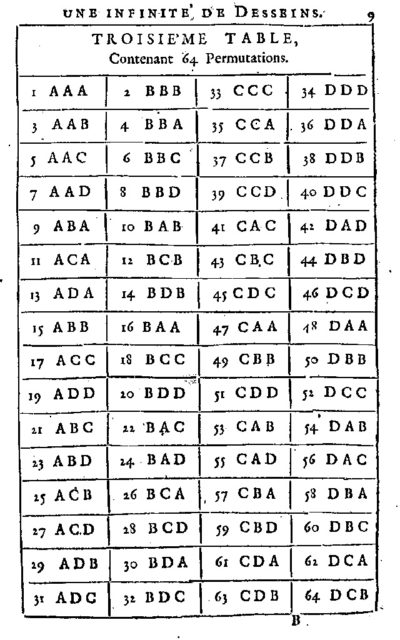
El siguiente análisis que se realiza es el de los posibles embaldosados con tres baldosas (en horizontal), que es igual a 4³ = 64 (cuatro posibilidades –A, B, C, D- para cada posición), como se muestra en la siguiente tabla.

Mientras que los posibles patrones de teselado con cuatro baldosas (en horizontal) son 4⁴ = 256. Aprovechemos este análisis para comentar cuales serían los posibles patrones de embaldosado de un pavimento cuadrado 2 x 2 utilizando cuatro baldosas cuadradas bicolor. Si pensamos en ello, podemos observar que tenemos cuatro posiciones posibles para nuestras baldosas, arriba a la izquierda, arriba a la derecha, abajo a la izquierda y abajo a la derecha, luego se trata de analizar las posibles formas de colocar baldosas de Truchet, con sus cuatro orientaciones (A, B, C y D) en esas cuatro posiciones. La solución es exactamente el análisis de Doüat, luego los posibles patrones de teselado del pavimento cuadrado 2 x 2 serían también 256.

Veamos algunos de estos patrones. Por ejemplo, si consideramos embaldosados del pavimento cuadrado 2 x 2 con las cuatro teselas distintas, es decir, aparecen las cuatro baldosas orientadas A, B, C y D, se obtienen 24 patrones de teselado distintos, las permutaciones de (A, B, C, D): ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB y DCBA. Y las ilustraciones (teselados concretos) que se corresponden con estos códigos de letras son los siguientes.

Estos son los 24 patrones de embaldosado con las cuatro baldosas distintas, pero si podemos repetir baldosas, llegamos hasta los 256 mencionados. Unos pocos más los mostramos en la siguiente imagen.

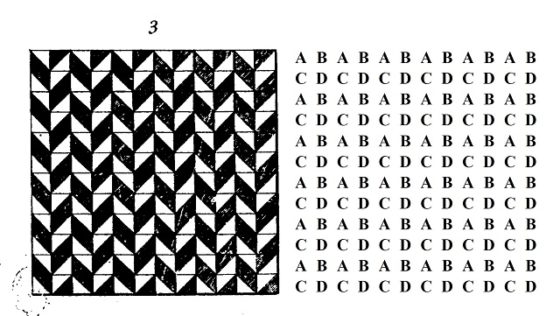
Cuanto más grande sea nuestro pavimento, más complejo será el análisis. A continuación, incluimos algunas ilustraciones de embaldosados de 12 x 12 baldosas pertenecientes al libro Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal, junto con su expresión mediante las letras A, B, C y D.

Respecto a la clasificación general de los patrones de embaldosado, claramente, la cantidad de patrones distintos para un pavimento con n baldosas es 4ⁿ, que podemos describirlas con las correspondientes cadenas de letras.

Los embaldosados de Truchet

Aunque el trabajo de investigación sobre los patrones de embaldosado con la sencilla tesela cuadrada de dos colores divididos por la diagonal lo inició el sacerdote dominico francés Sebastien Truchet (1657-1729) en su publicación Memoria sobre las combinaciones, publicada en Histoire de l’Académie Royale des Sciences de Paris, en 1704.

El propio Sebastien Truchet explica al inicio de su trabajo cómo se le ocurrió empezar a investigar la combinatoria de estos patrones de embaldosados:

Durante el último viaje que hice al canal de Orleans por orden de Su Alteza Real, en un castillo llamado Motte St. Lye, 4 leguas a este lado de Orleans, encontré varias baldosas de cerámica que estaban destinadas a embaldosar el suelo de una capilla y de varios otros apartamentos. Eran de forma cuadrada, divididas por una línea diagonal en dos partes coloreadas. Para poder formar diseños y dibujos agradables mediante la disposición de estas baldosas, primero examiné el número de formas en que estas baldosas podían unirse por parejas, siempre en disposición de damero […].

Desde el punto de vista histórico debemos de tener en cuenta que, aunque algunos conceptos y técnicas de la combinatoria se han estudiado desde la antigüedad, el origen de la combinatoria moderna podemos establecerlo en los siglos XVII y XVIII, gracias al trabajo de matemáticos como el francés Blaise Pascal (1623-1662), el alemán Gottfried Wilhelm Leibniz (1646-1716), quien publicara el texto De Arte Combinatoria (1666), el británico Isaac Newton (1643-1727), el suizo Jacob Bernoulli (1655-1705) o el suizo Leonhard Euler (1707-1783), quien inició o desarrolló el estudio de muchos ámbitos de la combinatoria (la teoría de grafos, los cuadrados greco-latinos, las particiones, el problema del recorrido del caballo, etc), entre otros. Por lo tanto, los trabajos de Sebastien Truchet y Dominique Doüat aparecieron en pleno desarrollo de la teoría de la combinatoria.

Claramente, la mejor forma de conseguir patrones hermosos –como podemos ver, por ejemplo, en muchos textos sobre diseños para quilts- es trabajar directamente con las baldosas cuadradas bicolor en las cuatro orientaciones (A, B, C y D), pero desde el punto de vista matemático trabajar con las letras, como hizo Doüat, permite un mejor análisis de las posibilidades combinatorias y ayuda a distinguir unas de otras, puesto que el listado de letras se convierte en el código que nos permite identificar cada embaldosado.

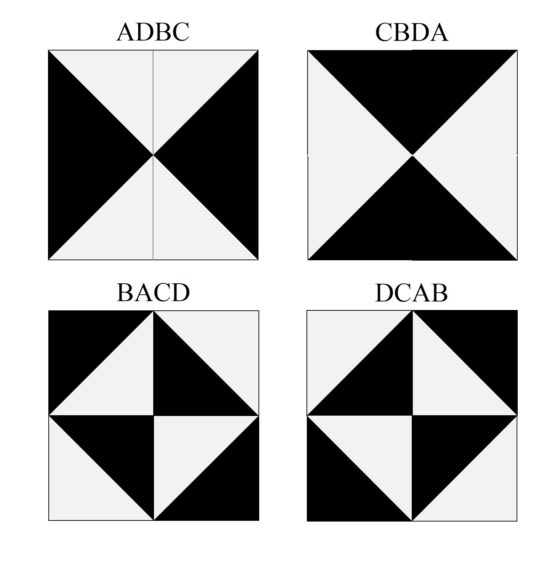
Otra cuestión que podemos tener en cuenta a la hora de estudiar los patrones de teselados es qué tipo de simetría tienen. Por ejemplo, si continuamos con los pavimentos cuadrados 2 x 2, aunque solo prestamos atención a los 24 patrones de embaldosado (de los 256 que hay en total) con las cuatro baldosas distintas que hemos descrito arriba, podemos observar que existen diferentes tipos de simetrías. Por ejemplo, los patrones ABCD, CDBA, BCAD y DACB se mantienen invariantes, es decir, no cambian, aunque realicemos rotaciones sobre ellos de 90, 180 o 270 grados. Tienen una simetría rotacional de 90 grados.

Los patrones ADBC, CBDA, BACD y DCAB se mantienen invariantes mediante rotaciones de 180 grados. Tienen una simetría rotacional de 180 grados. Aunque observemos que si realizamos un giro de 90 grados no se obtiene el mismo patrón, sino un patrón similar con cambio de los colores (girando 90 grados ADBC se obtiene CBDA y viceversa, y girando 90 grados BACD se obtiene DCAB y viceversa, que son patrones con los colores cambiados).

Otro tipo de simetrías que podemos considerar son las simetrías (especulares) respecto a una recta, es decir, lo que hay a un lado y a otro respecto a la recta es igual (su imagen especular, como si la recta fuera el espejo). Por ejemplo, el patrón DABC tiene simetría respecto a la recta vertical que pasa por el centro, como se muestra en la imagen.

En este sentido, tenemos que los patrones DACB y BCAD, que sabemos que tienen una simetría rotacional de 90 grados por lo visto anteriormente, tienen simetría especular respecto a cuatro rectas que pasan por el centro del cuadrado, las dos rectas horizontal y vertical, así como las dos diagonales del cuadrado.

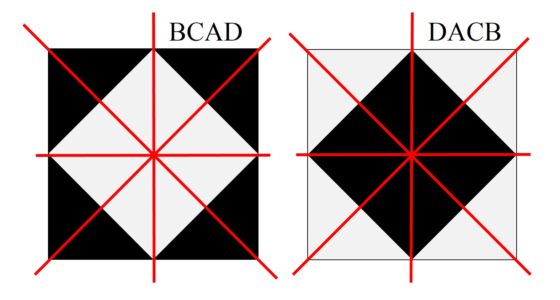
Los patrones BACD y DCAB tienen simetría especular respecto a las dos diagonales, los patrones ADBC y CBDA respecto a las rectas vertical y horizontal que pasan por el centro del cuadrado, los patrones ACBD, BDAC, CABD y DBCA respecto a la recta horizontal que pasa por el centro y BCDA, CBAD, DABC y ADCB respecto a la vertical que pasa por el centro. En total, catorce patrones son simetría especular respecto a rectas, los que aparecen en la siguiente imagen.

En resumen, de los 24 patrones de embaldosado con las cuatro baldosas distintas, tenemos que 16 tienen alguna simetría rotacional o especular, que son las “simetrías normales”, mientras que hay 8 patrones (los que vemos en la siguiente imagen) que no tienen ninguna de estas simetrías.

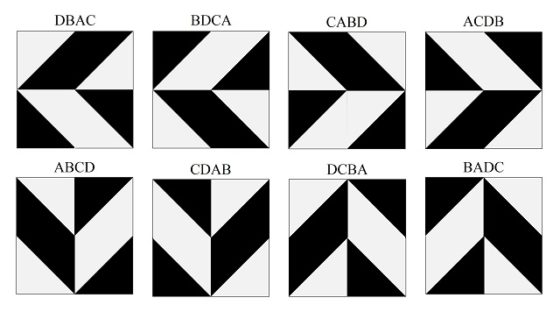
Vistos juntos estos 8 patrones, podemos percibir que tienen cierto tipo de simetría. En concreto, tienen simetría con cambio de color. Los cuatro primeros patrones tienen una simetría especular respecto a la recta horizontal que pasa por el centro, pero con cambio de color, es decir, las zonas que en un lado son blancas, en el lado opuesto son negras, y al revés. Mientras que los cuatro últimos patrones tienen una simetría especular respecto a la recta vertical que pasa por el centro.

En conclusión, todos los patrones de teselado para un pavimento cuadrado de tamaño 2 x 2 tienen simetría normal o simetría con cambio de color. Esta es precisamente la versión sencilla del conocido como teorema del diamante, que describimos a continuación.

Teorema del diamante

Teorema del diamante (versión 2 x 2): Sea D la figura formada por el diamante negro, construido con las cuatro orientaciones distintas de la baldosa bicolor de Truchet, que se muestra en la siguiente imagen:

Si G es el grupo de las 24 permutaciones de los cuatro cuadrados (baldosas) de D, entonces la imagen de D mediante cualquiera de los elementos del grupo G da lugar a una figura que tiene simetría normal o simetría con cambio de color.

Pero esta solo es una versión sencilla, que nos va a permitir entender mejor la versión normal, del verdadero teorema del diamante, que explicamos a continuación.

Sea ahora D la figura de cuatro diamantes negros sobre un cuadrado 4 x 4 que mostramos en la siguiente imagen y cuyo código de letras es DADACBCBDADACBCB,

y sea G el grupo de las 322.560 transformaciones generado por las permutaciones de dos filas cualesquiera del cuadrado 4 x 4, las permutaciones de dos columnas cualesquiera o las permutaciones de dos cuadrantes 2 x 2 cualesquiera. Por ejemplo, si a la figura D le aplicamos la permutación de las columnas del medio, luego la permutación de las filas del medio, después la permutación de los cuadrantes de abajo a la izquierda y de arriba a la derecha y finalmente la permutación de las dos filas exteriores, el resultado es la siguiente figura.

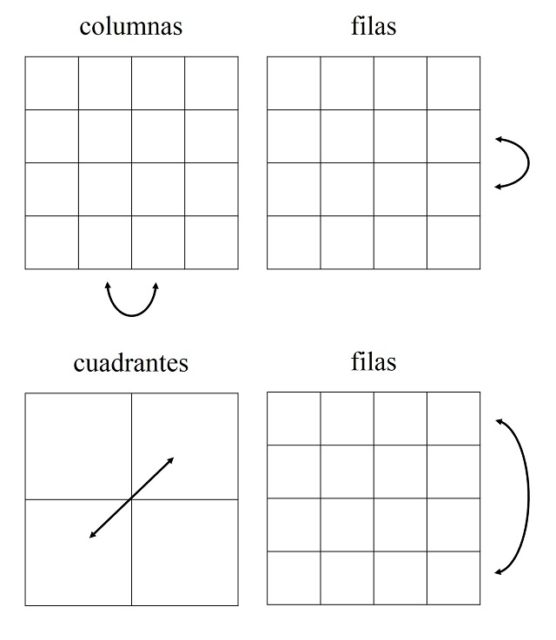
El teorema del diamante, del matemático estadounidense Steven H. Cullinane (1942), dice lo siguiente.

Teorema del diamante: Todas las imágenes que se obtienen mediante alguna de las 322.560 transformaciones del grupo G de la figura D tienen simetría normal o simetría con cambio de color.

Por ejemplo, la anterior imagen tiene simetría especular con cambio de color respecto a las rectas horizontal y vertical que pasan por el centro.

O la siguiente figura que se obtiene permutando las dos primeras filas, luego las dos columnas de la derecha, después el cuadrante de arriba a la izquierda con el de abajo a la derecha y finalmente, las dos columnas centrales, tiene una simetría rotacional de 180 grados con cambio de color.

O, por ejemplo, la siguiente figura tiene simetrías rotacionales y especulares.

Pero no hemos dicho cómo obtener la figura anterior a partir de la figura original de los cuatro diamantes negros. Este es un problema, o una diversión, que el propio Steven H. Cullinane plantea como rompecabezas y que bautiza con el nombre de “rompecabezas diamante 16”.

Rompecabezas diamante 16: Primero construir 16 baldosas bicolor de Truchet sobre cartulina, obtener alguna de las figuras de la columna de la izquierda, en la siguiente imagen, e intentar transformarla en la correspondiente figura de la columna de la derecha, utilizando las transformaciones del teorema del diamante, es decir, permutaciones de dos filas cualesquiera, de dos columnas cualesquiera o de dos cuadrantes 2 x 2 cualesquiera.

Si no queréis construir las teselas de Truchet y jugar con ellas al rompecabezas diamante 16, podéis hacerlo en la versión online que está incluida en la bibliografía.

Terminamos con la imagen de un quilt realizado utilizando un diseño de teselado con la estructura cuadrada bicolor, con los dos colores separados por la diagonal, la baldosa de Truchet.

Bibliografía:

1.- Cyril Stanley Smith (con la traducción del texto de Truchet por Pauline Boucher), The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy, Leonardo, vol. 20, n. 4, pp. 373-385, 1987.

2.- Dominique Doüat, Méthode pour faire une infinité de desseins différents avec des carreaux mi-partis de deux couleurs par une ligne diagonale : ou observations du Père Dominique Doüat, Religieux Carme de la Province de Toulouse, sur un mémoire inséré dans l’Histoire de l’Académie Royale des Sciences de Paris l’année 1704, présenté par le Révérend Père Sébastien Truchet religieux du même ordre, Académicien honoraire [Método para hacer una infinidad de diseños distintos con cuadrados de dos colores separados por una línea diagonal], París, 1922.

Facsímil (extractos) e introducción de Jacques André

Obra completa en Gallica – Bibliothèque nationale de France

3.- Sebastien Truchet, Memoir sur les Combinaisons, Histoire de l’Académie Royale des Sciences de Paris, 363-372 (1704).

Obra completa en Gallica – Bibliothèque nationale de France

4.- Steven H. Cullinane, The Diamond Theorem, eprint arXiv:1308.1075, 2013.

5.- Steven H. Cullinane, The Diamond Theorem

6.- 5.- Steven H. Cullinane, The Diamond 16 puzzle

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica