En la entrada del Cuaderno de Cultura Científica titulada Las bases de numeración o cómo hacer trucos de magia binarios hablamos de las distintas bases de un sistema de numeración posicional como el que nosotros utilizamos de forma habitual y cómo pasar de la representación posicional de un número natural (o entero) cualquiera en la base usual, la decimal, a otra base de numeración no decimal, y viceversa.

En particular, comentamos que dada una base de numeración b –ya sea esta igual a 2, 3, 10, 12 o 60- la representación posicional de cualquier número natural en la misma viene dada por una expresión d₁d₂…d_r (donde los dígitos d_i –para i entre 1 y r– pertenecen a la familia de las b cifras básicas del sistema de numeración, que tienen valores entre 0 y b – 1) teniendo en cuenta que el número puede escribirse, de forma única, como

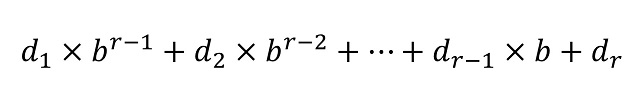
Así, el número que en la base decimal representamos como 3.457, es decir, que tiene el valor de 3 veces la cantidad de 1.000 (= 10³), 4 veces la cantidad de 100 (= 10²), 5 veces la cantidad de 10 (= 10¹) y 7 veces la unidad 1 (= 10⁰), tendrá diferentes representaciones en función de la base b elegida. Así, si tomamos el sistema binario (b = 2) el anterior número se representa como (110110000001)₂, ya que “3.457” = 2¹¹ + 2¹⁰ + 2⁸ + 2⁷ + 1; en la base octal (b = 8) como (6600)₈, porque “3.457” = 6 x 8³ + 6 x 8²; o en la base hexadecimal (b = 16), donde las cifras básicas son 0, 1, …, 9, A, B, C, D, como (D81)₁₆, puesto que “3.457” = D x 16² + 8 x 16 + 1, donde estamos utilizando el subíndice de las representaciones (2, 8 y 16) para recordar que esa es una representación en esa base de numeración.

En esta entrada vamos a estudiar la representación de cualquier número real, no solamente natural, es decir, que tiene parte “fraccionaria” (la que va a la derecha de la coma, como 1415 en el número 13,1415). Al igual que la representación en el sistema de numeración posicional de base b para los números naturales se basaba en la expresión de estos números en función de las potencias (no negativas) de la base b⁰, b¹, b², b³, … para los números reales, no enteros, es decir, aquellos con parte fraccionaria (“con coma”) la representación en la base b se basa en la expresión en función de todas las potencias de la base b, incluidas ahora las negativas b^-1 = 1/b, b^-2 = 1/b², b^-3 = 1/b³, …

El sistema de numeración babilónico

Para ilustrar el primer ejemplo, vamos a considerar el sistema de numeración posicional babilónico (véase la entrada ¿Sueñan los babilonios con multiplicaciones eléctricas?). Como menciono en mi libro Los secretos de la multiplicación, de los babilonios a los ordenadores (Catarata, 2019), hacia el 2.000 a. n. e. se introdujo en Babilonia el que parece ser el primer sistema de numeración posicional de la historia de la humanidad, el sistema sexagesimal de los eruditos babilonios, conocido por este nombre porque era el utilizado por matemáticos y astrónomos.

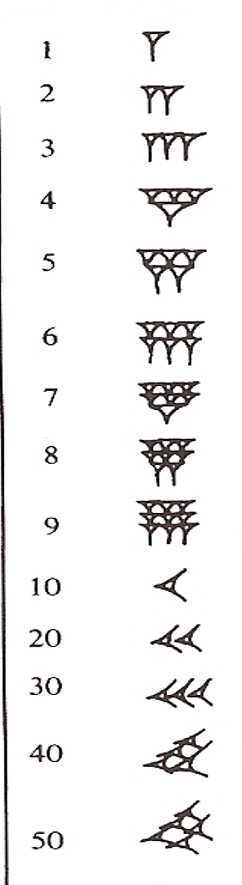
La primera diferencia con el sistema de numeración moderno es que este último es decimal, luego tiene diez cifras básicas, del 0 al 9, mientras que el sistema babilónico, al ser sexagesimal, necesitaba de sesenta cifras básicas. Durante mucho tiempo no existió un símbolo para el cero y simplemente dejaban un hueco vacío, lo cual creaba cierta confusión. Las 59 cifras del sistema de numeración babilónico, excluido el cero, no eran todas diferentes, como ocurre en el sistema moderno, sino que su notación se basaba en la acumulación de unidades, que eran los clavos verticales, y decenas, que eran espigas, como se ve en la siguiente imagen, heredados de los números cuneiformes sumerios. Cuando se empezó a representar el cero, se hizo como un doble clavo inclinado o una doble espiga, con un tamaño más pequeño que el de las otras cifras.

Así, el número que nosotros representamos como 1.859, en la base decimal, los babilonios lo representaban, como se observa en la siguiente imagen, como tres espigas, es decir, 30, seguido de cinco espigas y nueve clavos, es decir, 59, puesto que 1.859 = 30 x 60 + 59. En esta entrada, para no tener que dibujar los clavos y las espigas, escribiremos que es el número de dos dígitos [30; 59] en el sistema babilónico.

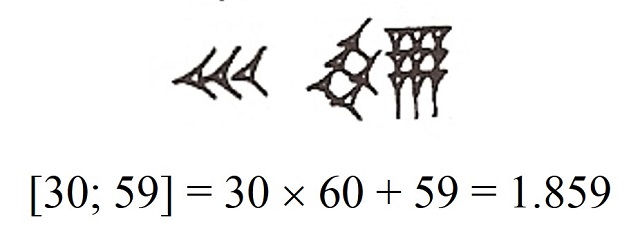
Por ejemplo, dos números que se representan en la tablilla de arcilla BM13901, que se conserva en el Museo Británico de Londres y que es uno de los textos matemáticos babilónicos más antiguos, son 64.000 y 424.000. El primero, 64.000, está representado como [17; 46; 40], aunque con las cifras babilónicas de clavos y espigas, es decir, 17 x 60² + 46 x 60 + 40, mientras que el segundo, 424.000, está representado como [1; 57; 46; 40], esto es, 1 x 60³ + 57 x 60² + 46 x 60 + 40.

Los babilonios también manejaron los números racionales, las fracciones. Como ya hemos recordado más arriba, las cifras a la derecha de la coma expresan las potencias negativas de la base b. Así, el número racional 23,14, en nuestro sistema de numeración posicional decimal, tiene el valor 3,14 = 3 + 1 x 0,1 + 4 x 0,01 = 3 + 1 x 10^–1 + 4 x 10^–2. Mostremos un ejemplo para los números babilónicos.

La tablilla de arcilla babilónica YBC7289, de la Universidad de Yale, contiene la aproximación de la raíz de 2 siguiente [1; 24; 51; 10], que está expresada en el sistema de numeración babilónico (en su versión original con clavos y espigas), cuyo valor sería: 1 + 24 x 60^–1 + 51 x 60^–2 + 10 x 60^–3 = 1,41421296… aunque la notación babilonia respecto al lugar donde se sitúa la coma era confusa, y solo el contexto del problema o la situación la resolvían.

Expresión decimal de un número

Al igual que en el ejemplo anterior, del sistema de numeración babilónico, obtener la expresión decimal de un número real, que tiene parte fraccionaria, es sencillo. Veamos algunos ejemplos.

Consideremos el siguiente número racional expresado en base binaria como

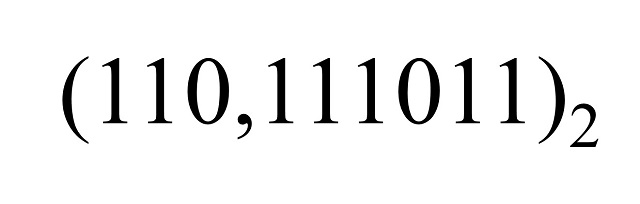
Para ver cuál es el valor de este número binario necesitamos las potencias de 2. Por una parte, las no negativas, 2² = 4, 2¹ = 2, 2⁰ = 1, para los tres dígitos de la izquierda de la coma, y las negativas, 2⁻¹ = 1∕2 = 0,5; 2⁻² = 1∕4 = 0,25; 2⁻³ = 1∕8 = 0,125; 2⁻⁴ = 1∕16 = 0,0625; 2⁻⁵ = 1∕32 = 0,03125 y 2⁻⁶ = 1∕64 = 0,015625, para los dígitos de la derecha de la coma.

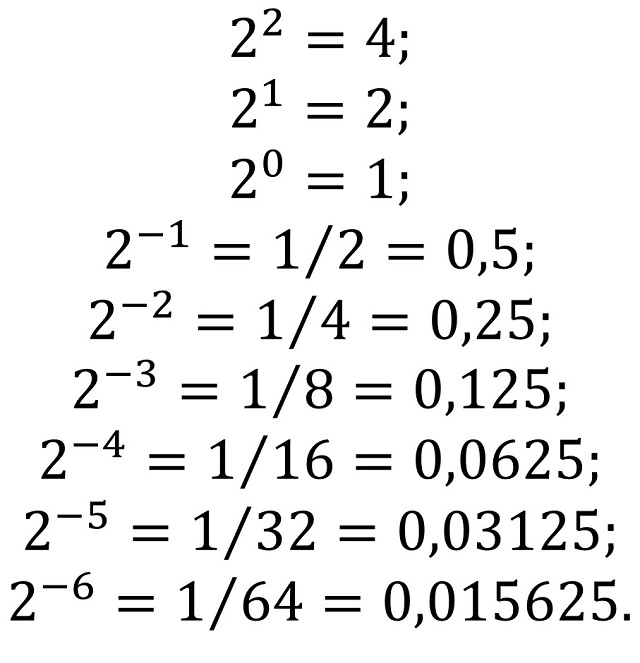
Por lo tanto, el número binario (110,111011)₂ tiene el valor de 6,921875 (expresado en el sistema decimal), ya que:

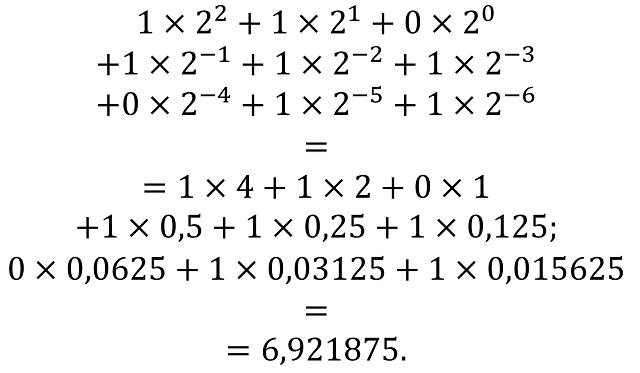
Veamos un nuevo ejemplo para la base b = 4, en concreto, consideremos el número que en base 4 se escribe como (3,021003331)₄. Para ver su valor, la expresión en el sistema decimal, necesitamos las potencias negativas de 4, desde – 1 hasta – 9, que aparecen en la siguiente imagen.

Por lo tanto, el número (3,021003331)₄ toma el valor 3.141590118408203125, ya que:

Como podemos observar el número racional dado por la expresión (3,021003331)₄ es una aproximación al número pi, en base 4. Si hubiésemos tomado (3.02100333122220202011)₄ tendríamos una mejor aproximación 3.14159265358921402366.

Conversión de la base decimal a otra base

Como en la entrada anterior, empecemos por la base binaria, b = 2. Si tenemos un número con parte fraccionaria, en la base decimal, y queremos pasarlo a la base binaria, sabemos que tenemos que expresarlo en función de las potencias de 2. Por ejemplo, tomemos el número 0,375. Como las potencias de 2 negativas son 2⁻¹ = 1∕2 = 0,5; 2⁻² = 1∕4 = 0,25; 2⁻³ = 1∕8 = 0,125; 2⁻⁴ = 1∕16 = 0,0625; 2⁻⁵ = 1∕32 = 0,03125 y 2⁻⁶ = 1∕64 = 0,015625, etc, entonces si vemos cómo escribir ese número como suma de estas podemos ver que

0,375 = 0,25 + 0,125 = 2⁻² + 2⁻³

luego el número decimal 0,375 se escribe en base binaria como (0,011)₂.

Aunque, al igual que vimos para los números naturales, podemos desarrollar un algoritmo para determinar la expresión binaria del número. Si el número que queremos convertir en binario tiene parte no fraccionaria (por ejemplo, en 197,703125 sería el 197), para esa parte utilizaremos el algoritmo visto en la entrada Las bases de numeración o cómo hacer trucos de magia binarios, que consiste en dividir por 2 e ir considerando los restos. Como vimos en esa entrada el número 197 se expresa en la base binaria como (11000101)₂. Mientras que para la parte fraccionaria (en nuestro ejemplo sería 0,703125) utilizaremos un algoritmo basado en dividir por 0,5 = 1/2 = 2^–1. Veámoslo con un ejemplo.

El algoritmo consiste en dividir nuestro número 0,703125 por 0,5 (que es como multiplicar por 2), si lo hacemos nos queda 1,40625. De este nos quedamos la unidad 1, que nos va a aportar un 1 en la representación binaria, y volvemos a dividir 0,40625 por 0,5. Al hacerlo nos queda 0,8125, que nos aporta un 0 en la representación binaria y lo volvemos a dividir por 0,5. En total:

De donde la expresión binaria de 0,703125 es (0,101101)₂. El motivo es que este procedimiento nos permite obtener la expresión del número en función de las potencias de 2 negativas, como vemos en la siguiente imagen.

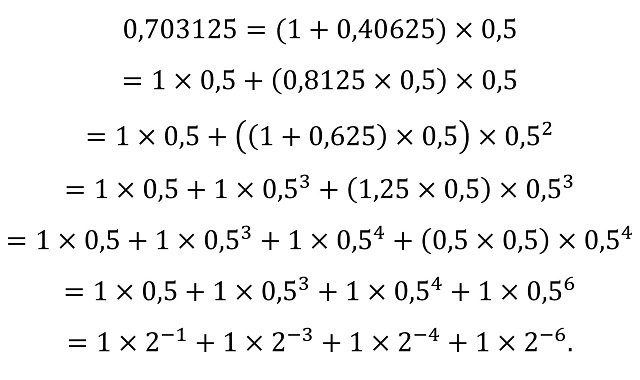
En conclusión, el número (decimal) 197,703125 se expresa en la base binaria como (11000101,101101)₂.

Al igual que lo hemos hecho para la base binaria lo podríamos hacer para cualquier otra base.

Un patrón artístico en base cuatro

En la entrada del Cuaderno de Cultura Científica titulada El arte de la sencilla baldosa de Truchet utilizábamos los primeros dígitos del número pi en base 4 (con las cuatro cifras básicas 1, 2, 3, 0) para crear un patrón de embaldosado particular que pudiésemos utilizar para crear una pintura abstracta. Vamos a terminar esta entrada con una idea similar, creando otro patrón basado en la expresión de la raíz de 2 en base 4.

Los primeros 12 x 12 = 144 dígitos del número raíz de 2 en base 4 son los siguientes (que yo he obtenido con un conversor online de la Université Cote d’Azur).

Además, ahora las cuatro orientaciones de la baldosa cuadrada de Truchet que asociamos a las cuatro cifras básicas, 1, 2, 3, 0, son las que se muestran en la imagen (en esta ocasión le hemos añadido color).

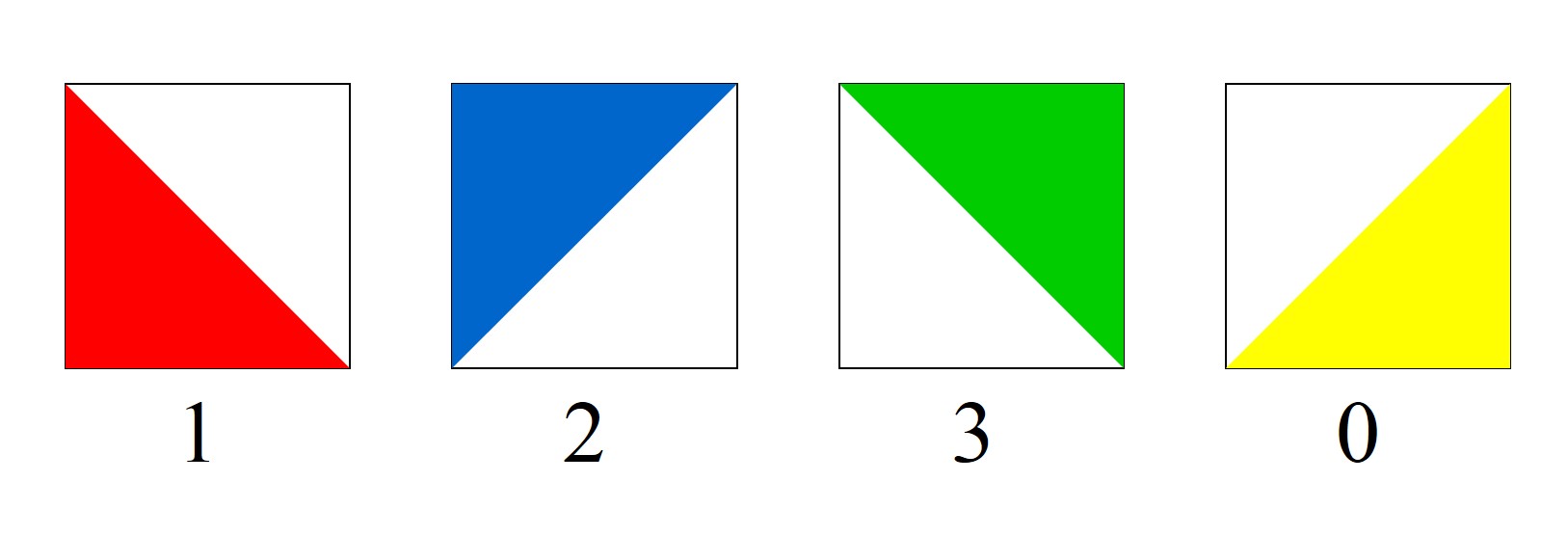
Por lo tanto, el patrón de teselado con las cuatro orientaciones de la baldosa de Truchet basado en el número raíz de 2, en base 4, es el siguiente.

Bibliografía:

1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica