Una de las cosas que más me sorprende cuando leo sobre cuadrados mágicos, además de la belleza matemática de los mismos, es la enorme cantidad de métodos que existen para construirlos, así como el gran interés que han despertado en grandes matemáticos como el francés Pierre de Fermat (1607-1665), el suizo Leonhard Euler (1707-1783), el británico Arthur Cayley (1821-1895) o el indio Srinivasa Ramanujan (1887-1920).

Aunque es un concepto matemático bastante conocido, recordemos qué es un cuadrado mágico. Un cuadrado mágico de orden n es una distribución de los primeros n² números (aunque, de forma general, puede ser una colección cualquiera de n² números) sobre las casillas de un retículo cuadrado n × n, de forma que la suma de los números de cada fila, cada columna y cada diagonal principal sea siempre la misma, la cual se conoce con el nombre de constante mágica.

En esta entrada del Cuaderno de Cultura Científica vamos a mostrar algunos métodos para construir cuadrados mágicos. Existen diferentes tipos de métodos en función de si el orden es par o impar.

Empecemos con los cuadrados mágicos de orden impar. En la entrada Habibi y los cuadrados mágicos II ya construimos todos los cuadrados mágicos de orden 3, que son solamente ocho, pero que, salvo simetrías, son todos iguales, luego solo hay un cuadrado mágico de orden 3, el conocido Lo-Shu (por filas, 4, 9, 2; 3, 5, 7; 8, 1, 6).

Colocación en diagonal

En general, para los órdenes impares, uno de los métodos más antiguos es el método de colocación en diagonal, que ha recibido muchos nombres. Como podemos leer en el libro Magic Squares, Their History and Construction from Ancient Times to AD 1600 (véase la bibliografía), en un principio se le conocía como el método de Bachet, por el matemático, lingüista, filósofo y poeta francés Claude Gaspard Bachet de Méziriac (1581-1638), del que ya hablamos en la entrada Un problema clásico de pesas, quien lo presentó en la segunda edición (1624) de su libro de matemática recreativa Problèmes Plaisants et Délectables, qui se font par les nombres – Problemas placenteros y deliciosos que se plantean con los números (1612). Después se le llamó método de Cardano, ya que resultó que también aparecía explicado en el libro de aritmética Practica arithmetica et mensurandi singulares / Aritmética práctica y medidas singulares (1539) del matemático italiano Gerolamo Cardano (1501-1576). Cuando se conoció la existencia de un libro sobre cuadrados mágicos del comentarista y gramático bizantino Manuel Moschopoulos (siglos XIII-XIV) en el que se explicaba, se le atribuyó al mismo la autoría de esta construcción. Aunque su origen parece estar antes del siglo XI, que es cuando el matemático, astrónomo y físico árabe Alhacén –Abū ‘Alī al-Hasan ibn al-Hasan ibn al-Háytham– (965-1040) dio una justificación de esta construcción.

En este método, como en muchos otros, se van colocando los números desde 1 hasta n² de una forma, más o menos, continua. En concreto, esta construcción para ordenes impares se basa en dos reglas (que vemos en el caso particular de orden 5 en la siguiente imagen):

i) se escribe el número 1 en una de las cuatro casillas adyacentes a la casilla central y se van colocando los siguientes números (2, 3, 4, …) en un recorrido diagonal (en el ejemplo de la imagen es un movimiento diagonal descendente hacia la derecha) a partir de la casilla del número 1, de forma que cuando se llega a un lado de la retícula se continúa por el lado opuesto (podemos valernos de filas y columnas auxiliares para apoyarnos en el movimiento diagonal y saber en qué casilla debemos continuar en los lados opuestos);

ii) cuando la siguiente casilla, en el movimiento diagonal, esté ocupada (lo cual ocurre cada n casillas), pasaremos a la casilla que está dos lugares más abajo y continuaremos el movimiento diagonal.

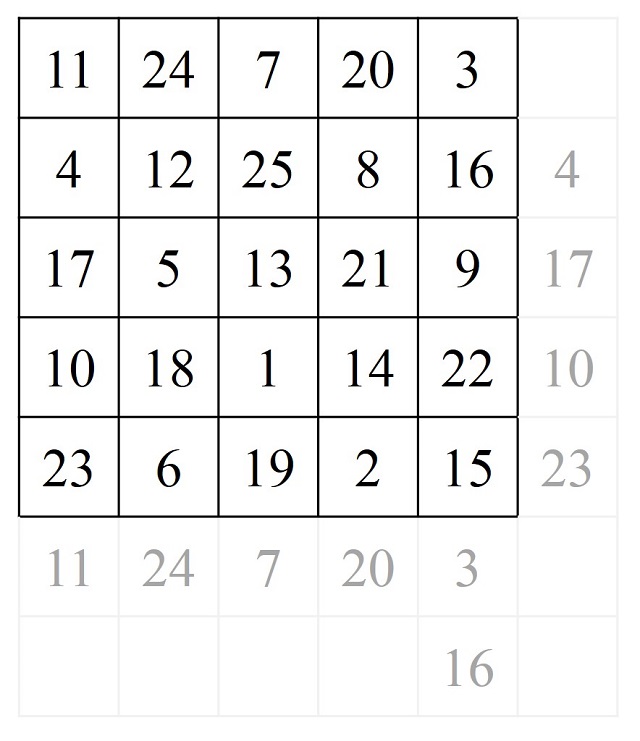
Una de las curiosas propiedades de esta construcción es que es simétrica, en el siguiente sentido. Dos números que están en posiciones simétricas respecto a la casilla central suman n² + 1, como 18 y 8, 24 y 2, 5 y 21, que suman 26. Además, la casilla central es el número que está en la mitad, entre 1 y n², es decir, (n² + 1) / 2 (en el ejemplo, el número 13).

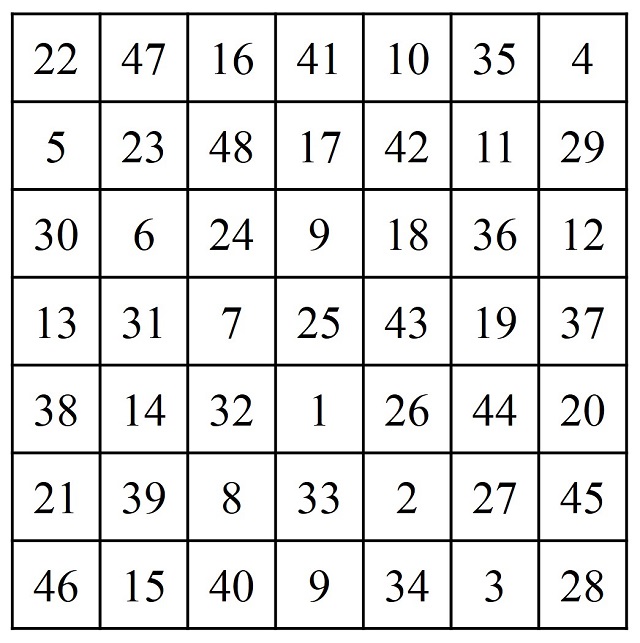
Según el texto anterior, este es el método más extendido y el primero en introducirse en Europa, que dio lugar a los tres cuadrados mágicos utilizados por entonces, de órdenes 5, 7 y 9 (dejando aparte el orden 3), que son los cuadrados mágicos asociados con Marte (orden 5), Venus (orden 7) y la Luna (orden 9), según las antiguas creencias astrológicas (véase Habibi y los cuadrados mágicos III).

Forma alternativa de Alhacén

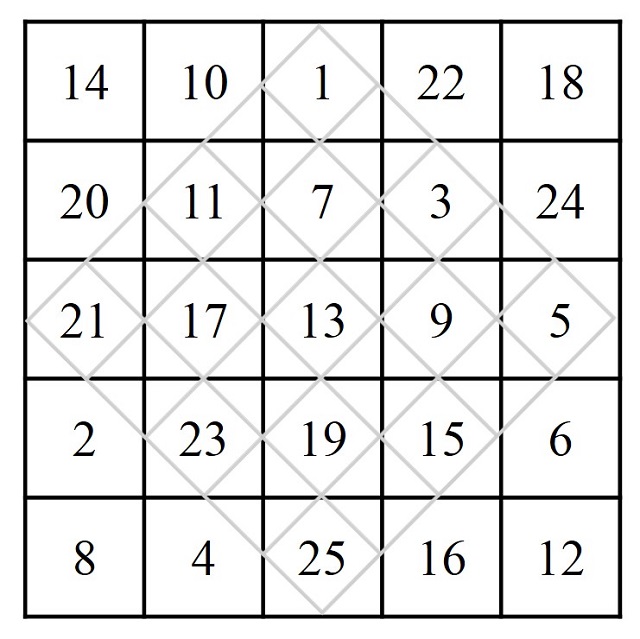
Sin embargo, Alhacén ofrece una forma alternativa para esta construcción de cuadrados mágicos de orden impar, para la cual se necesitaba un primer retículo cuadrado con los números escritos en orden natural y otro retículo auxiliar para desplazar los números del primero sobre el mismo y obtener así el cuadrado mágico antes descrito. Para empezar, si vamos a generar el cuadrado mágico de orden impar n, se parte de un retículo cuadrado n x n, sobre el que se superpone otro retículo n x n más pequeño y girado 45 grados, de forma que sus vértices estén sobre la mitad de los lados del primer retículo (como se muestra en la imagen).

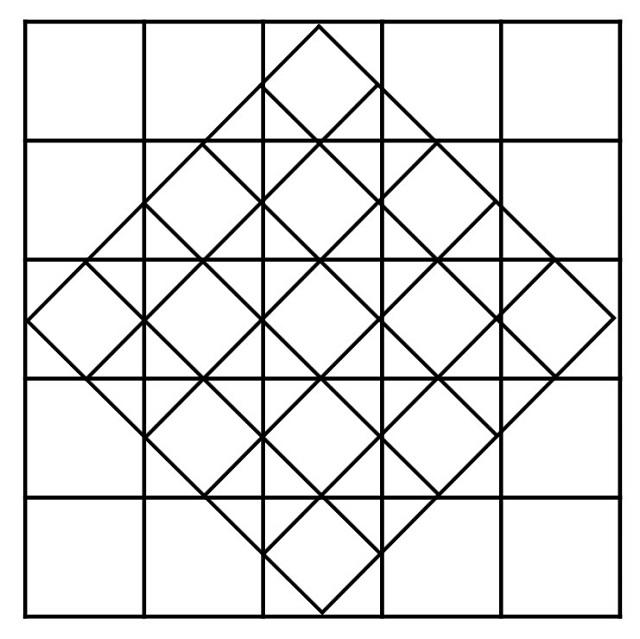
Luego se escriben los números del 1 al n² en orden natural sobre el primer retículo cuadrado, de forma que podemos observar cómo algunos números quedan sobre casillas del retículo inclinado superpuesto (3, 7, 8, 9, 11, 12, 13, 14, 15, 17, 18, 19 y 23), que van a considerarse que son los números que van a ir en esas casillas del nuevo retículo.

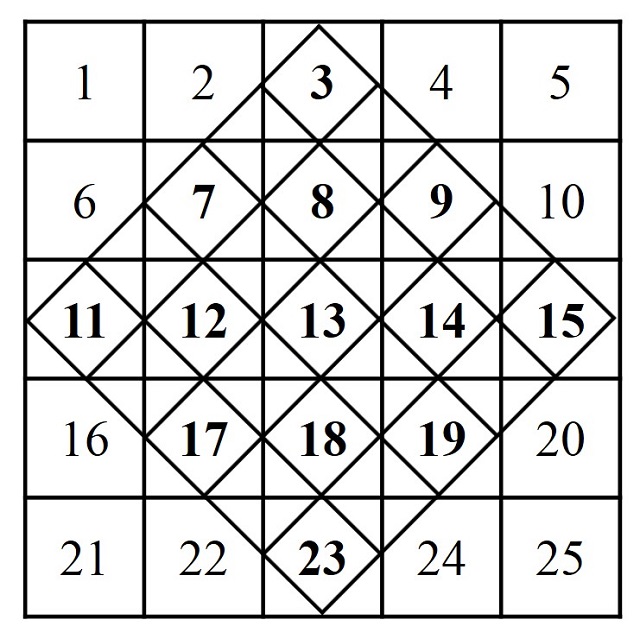
Finalmente, los números de las esquinas, que no están en el retículo inclinado se van a desplazar para colocarse dentro de las casillas del mismo. Así, el trío de números 1, 2 y 6, que está en la esquina superior izquierda, se va a desplazar diagonalmente hasta el lado opuesto del retículo inclinado. Lo mismo para los tríos de números de las otras tres esquinas, la esquina superior derecha (4, 5, y 10), la esquina inferior izquierda (16, 21 y 22) y la esquina inferior derecha (20, 24 y 25).

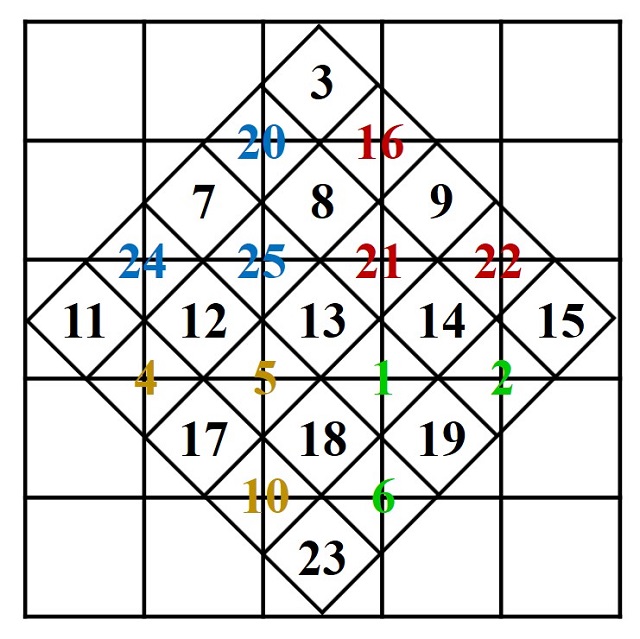
De manera que los números que están en el retículo 5 x 5 inclinado forman el cuadrado mágico de orden 5 relacionado con el planeta Marte que habíamos construido previamente, como puede comprobarse fácilmente.

Separación por paridad

Antes de pasar a ver algún método para ordenes pares, vamos a presentar un método que es el recíproco de la versión árabe, que acabamos de presentar, del método de colocación en diagonal, que se conoce como el método de separación por paridad.

Como en el caso anterior, empezamos con dos retículos n x n superpuestos, uno más pequeño y girado 45 grados, de forma que sus vértices estén sobre la mitad de los lados del primer retículo. Sin embargo, ahora se escriben los números del 1 al n² en orden natural sobre el retículo inclinado.

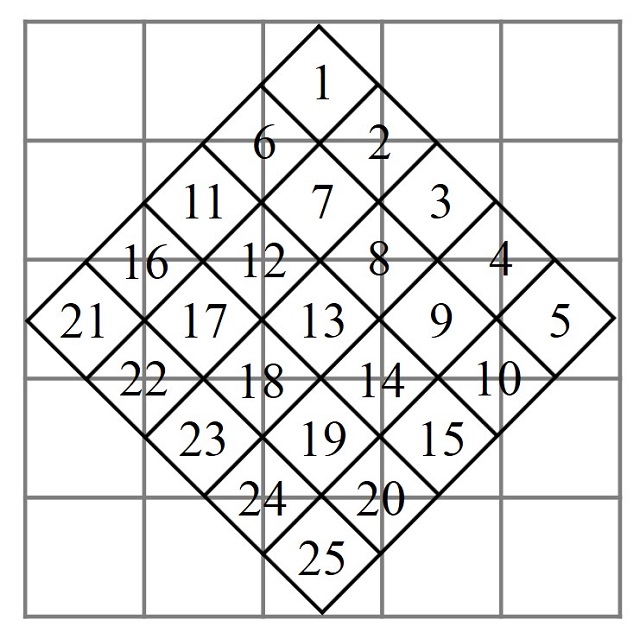
De forma paralela al proceso anterior, pero a la inversa, vamos a considerar los números del retículo inclinado que están en casillas del retículo grande, que son los números impares, y quedarnos con ellos en este retículo. Y los que no están dentro de una casilla del retículo grande, que son los números pares, los vamos a desplazar de forma inversa al proceso anterior. Por ejemplo, la terna de números pares 2, 4 y 8, que están arriba a la derecha del retículo inclinado, van a desplazarse diagonalmente hasta la esquina inferior izquierda del retículo grande. Lo mismo para las ternas 6, 12 y 16; 10, 14 y 20; y 18, 22 y 24, que se desplazan hacia las esquinas opuestas. Nos queda un cuadrado mágico de orden 5 diferente al anterior. En este las esquinas son números pares, como en el Lo-Shu (de orden 3).

Este método aparece en el texto Muntaha al-idrak fi taqasim al-aflak (La comprensión definitiva de las divisiones de las esferas) del matemático y astrónomo persa Al-Kharaqī, Abu Muḥammad ‘Abd al-Jabbar al-Kharaqi (1084-1158/9), quien lo atribuye al matemático Al-Isfizari, más joven que él, y lo denomina “método de los nudos y saltos”.

Como en esta construcción se separan los números por su paridad, pares e impares, se puede dar otra forma de construirlo, que aparece también en otros tratados de la época. Se trata de rellenar dos retículos inclinados con los números pares e impares por separado, como se muestra en la imagen.

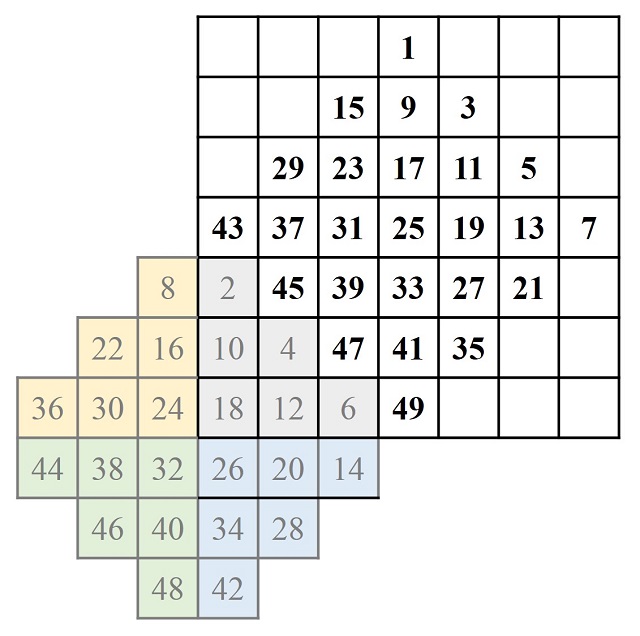
Ahora se trataría de dividir el retículo inclinado de los números pares en cuatro partes y cada una iría a una esquina, la que se corresponde con su forma.

Punteado

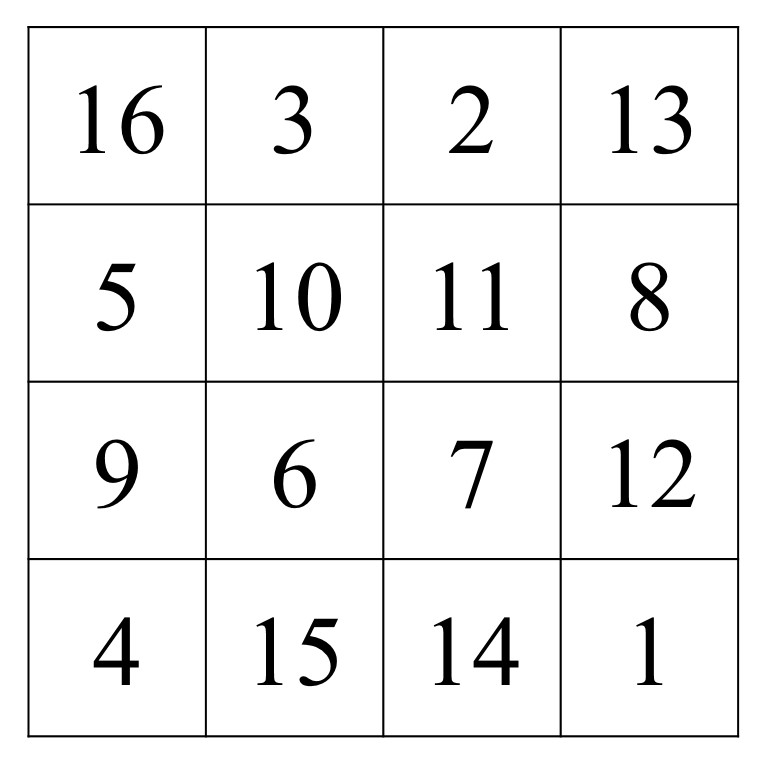
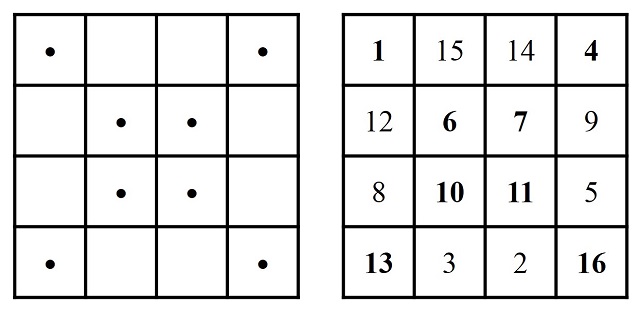
Para continuar vamos a volver a explicar, pero de una forma un poco diferente, uno de los métodos que vimos en la entrada Habibi y los cuadrados mágicos II. Se trata del método del punteado, para órdenes que son múltiplos de 4. Para el orden 4 se toma un retículo cuadrado 4 x 4 vacío y se colocan puntos en las casillas de la diagonal (como se muestra en la siguiente imagen). Entonces, se empiezan a contar las casillas, desde arriba a la izquierda, y si hay punto en la casilla se coloca el número que corresponde, pero si no hay no se pone nada. Cuando se llega a la última casilla se realiza el mismo procedimiento, pero en sentido inverso, empezando en esa última casilla, y colocando ahora los correspondientes números en las casillas sin puntos.

Este método se extiende a cualquier orden de la forma 4k. Para ello se divide el retículo 4k x 4k en k sub-retículos 4 x 4 y a cada retículo 4 x 4 se le colocan puntos en las diagonales (en la siguiente imagen vemos el orden 8 = 4 x 2).

Y el proceso de rellenarlo con números es el mismo, contar las casillas en una dirección y luego en la contraria y poniendo los correspondientes números en las casillas con puntos en el primer recorrido y en las casillas sin puntos en el segundo (para orden 8 nos queda el siguiente cuadrado mágico).

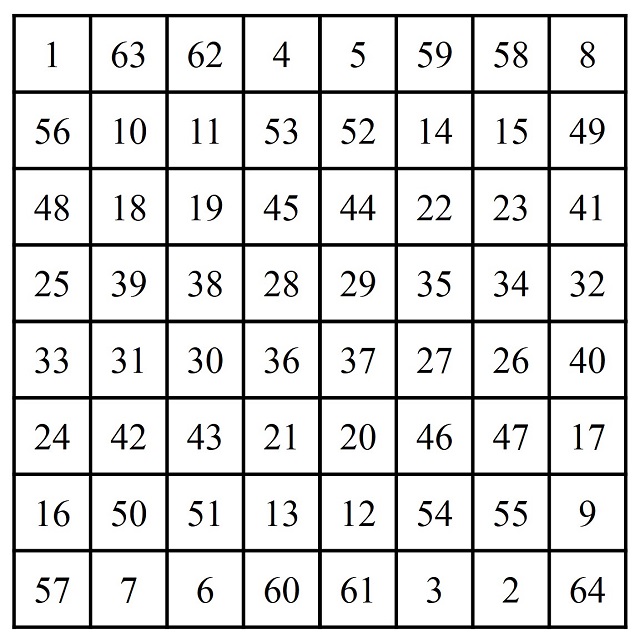
Para la explicación alternativa que dimos en la entrada Habibi y los cuadrados mágicos II la estructura de puntos es la misma, pero allí escribíamos todos los números en orden y luego desplazábamos, haciendo un giro de 180 grados alrededor del centro del retículo cuadrado, los números que no están en casillas punteadas. Véase, por ejemplo, en el orden 4 que el resultado es el mismo (así los números 2 y 3 que estaban en las casillas centrales de arriba pasan, al realizar el giro de 180 grados, a las casillas centrales de abajo, en el orden 3 y 2, y así para el resto).

Según un manuscrito árabe del siglo XII, que recoge este método y otros del matemático Alhacén, describe a este matemático árabe como uno de los mejores autores sobre el tema de los cuadrados mágicos.

Intercambio de sub-retículos

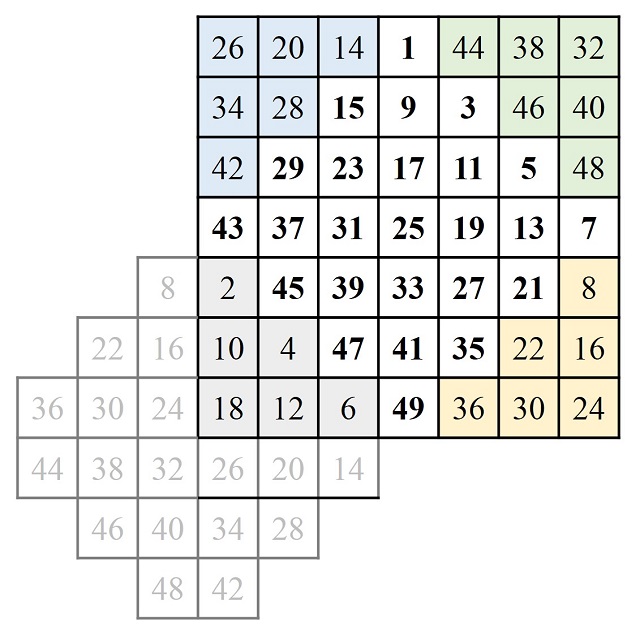
Existe otro método, que se conoce como método de intercambio de sub-retículos, que se basa en el método del punteado para orden 4 (con la interpretación del giro de 180 grados) y se utiliza para generar cuadrados mágicos de orden 4k. Se toma el retículo cuadrado 4k x 4k y se divide en 16 sub-retículos k x k y se colocan todos los números del 1 al (4k)² en orden natural, empezando por la casilla de arriba a la izquierda (véase imagen para k = 3).

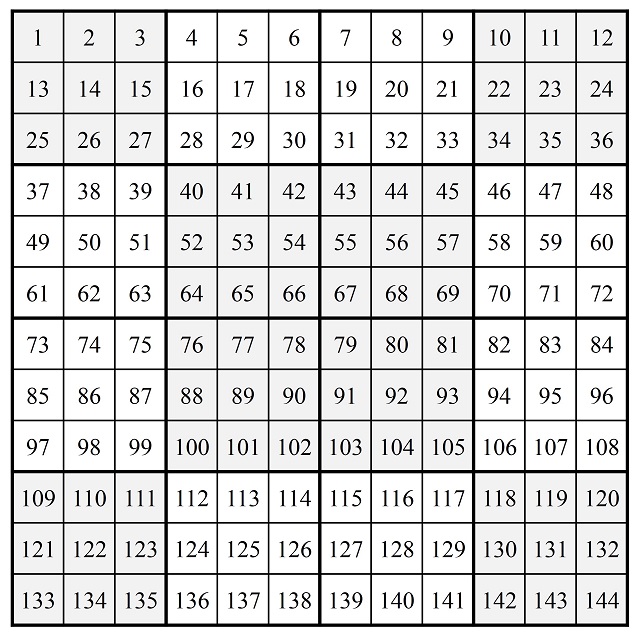
Hemos sombreado los sub-retículos k x k que se corresponderían con los puntos del retículo 4 x 4, es decir, los de las diagonales. Y para finalizar se actúa como en el caso del método de punteado para orden 4, en la versión del giro de 180 grados. Por lo tanto, los sub-retículos 4 x 4 sombreados se quedan como están, mientras que los no sombreados se mueven en un giro de 180 grados alrededor del centro del retículo. Para k = 3, es decir, orden 12, se obtiene el siguiente cuadrado mágico.

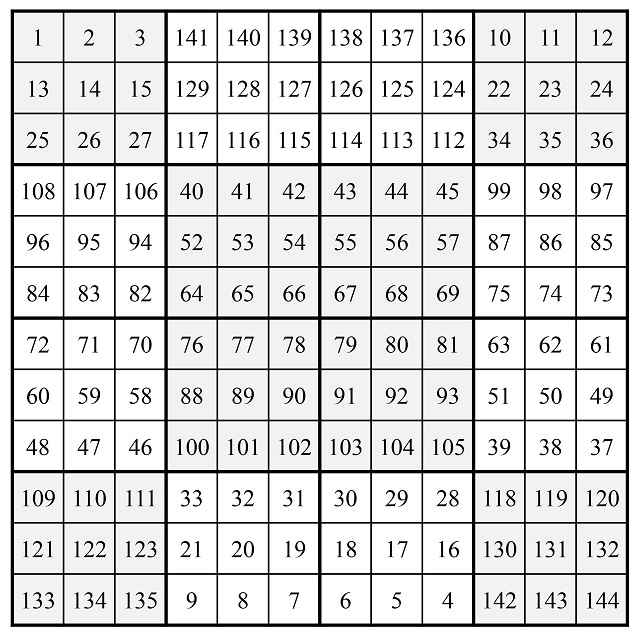
Rellenado continuo

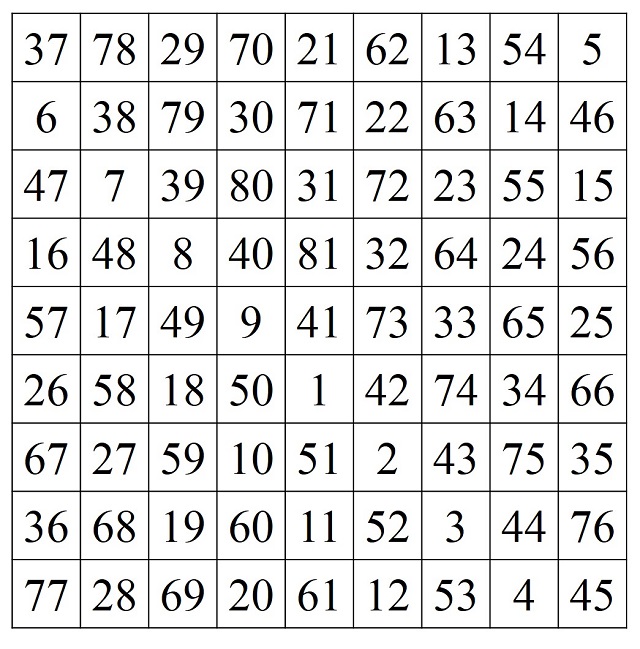
Y vamos a mostrar un método más para los órdenes múltiplos de 4, el método del rellenado continuo. Consiste en ir colocando los números por pares (excepto al principio y al final de las líneas) de forma alterna en filas opuestas. Por ejemplo, para orden igual a 12, se empieza con 1 en la primera fila, después 2 y 3 en la última fila, luego 4 y 5 en la primera fila, 6 y 7 en la última, 8 y 9 en la primera, 10 y 11 en la última, y finalmente 12 en la primera. Ahora se pasaría a las filas segunda y anteúltima, y se irían colocando los siguientes números, pero ahora de derecha a izquierda, y empezando por la anteúltima fila. Es decir, se cambia el sentido de colocación de los números, de izquierda a derecha o de derecha a izquierda, al cambiar de pareja de filas opuestas, así mismo se alterna la fila por la que se continúa contando, de arriba o de abajo. En la siguiente imagen vemos el resultado para orden igual a 12.

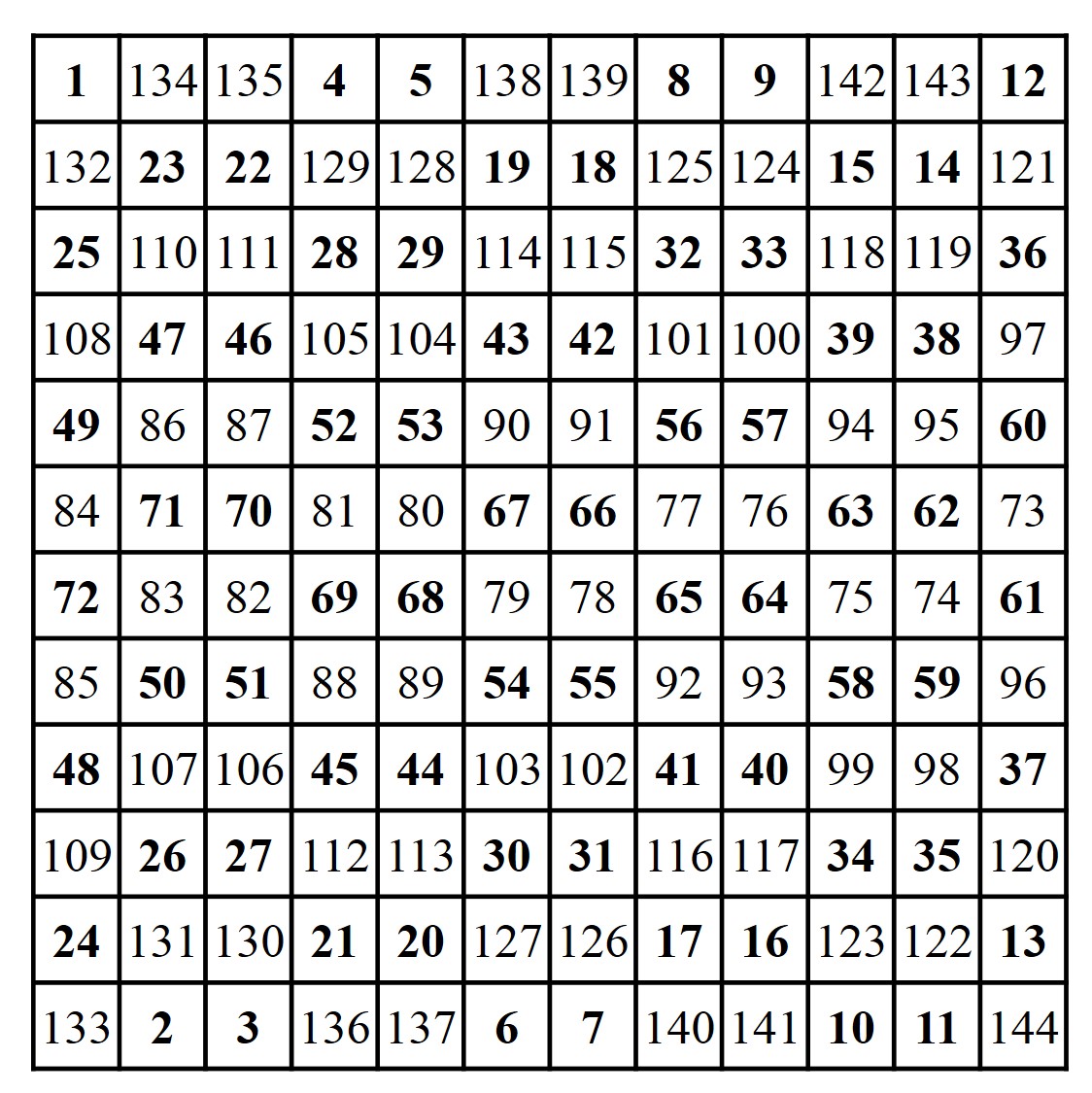
Nótese que al llegar a la mitad del retículo se intercambian las filas de posición.

Cambios en el retículo natural

Y vamos a terminar con un método para los órdenes de la forma 4k + 2, que son los órdenes pares que nos faltaban, es el método de cambios en el retículo natural, que también se debe al persa Al-Kharaqī (alrededor del año 1100), y que está relacionado, en cierta medida, con el método del punteado, aunque ahora tenemos puntos, ceros y cruces.

Vamos a ilustrar el caso más sencillo, un cuadrado mágico de orden 6 = 2 x 3. El retículo cuadrado 6 x 6 lo vamos a dividir en cuatro sub-retículos 3 x 3. En la primera casilla del primero colocamos un punto, en la segunda un cero y en la tercera una cruz, entonces completamos la diagonal principal con puntos y con ceros y cruces las diagonales quebradas cuya casilla inicial es un cero o una cruz.

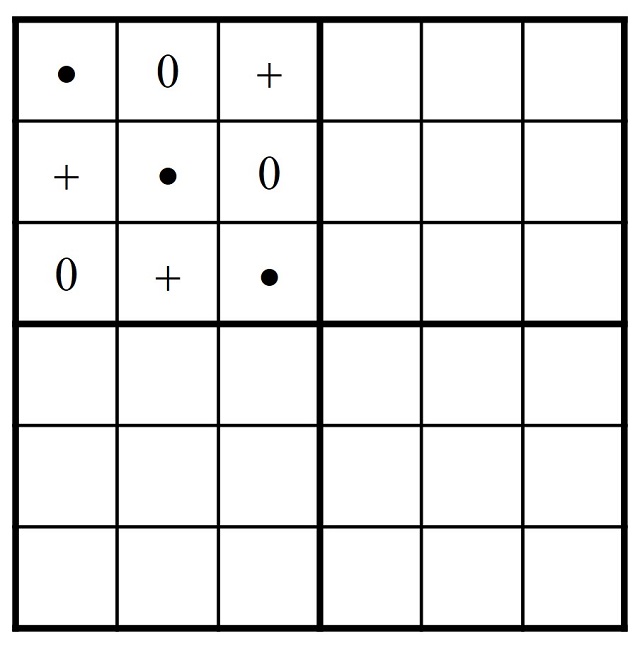
Ese primer sub-retículo nos va a servir de base para completar los otros tres sub-retículos. El que está a su derecha será su imagen especular respecto al segmento vertical que las separa, pero incluyendo solo puntos y cruces, el sub-retículo que está debajo suyo será su imagen especular respecto al segmento horizontal que los separa, pero incluyendo solo puntos y ceros, y el sub-retículo opuesto será su imagen mediante la rotación de 180 grados, respecto al centro del retículo, pero incluyendo solo los puntos.

Si estuviésemos en orden 10 el contenido de las casillas de la primera fila del primer sub-retículo 5 x 5 sería punto, nada, cero, cruz y punto, luego el esquema inicial sería ahora el siguiente.

Para el orden 14 el contenido de las casillas de la primera fila del primer sub-retículo 7 x 7 sería punto, nada, cero, cruz, punto, nada y punto. En general, en la primera fila del primer sub-retículo solo puede haber un cero y una cruz, mientras que al aumentar el tamaño aumenta el número de puntos de esa primera fila.

Una vez que se tiene el esquema inicial hay que colocar los números de forma continua. Se empieza en la casilla de arriba a la izquierda, que es un punto, y se van contando las casillas de forma normal (de arriba abajo y de izquierda a derecha) de forma que si aparece un punto se coloca el correspondiente número, después se realiza la misma operación en sentido contrario y empezando en la última casilla (casilla de abajo a la derecha), pero esta vez se colocan los correspondientes números en las casillas donde no hay nada.

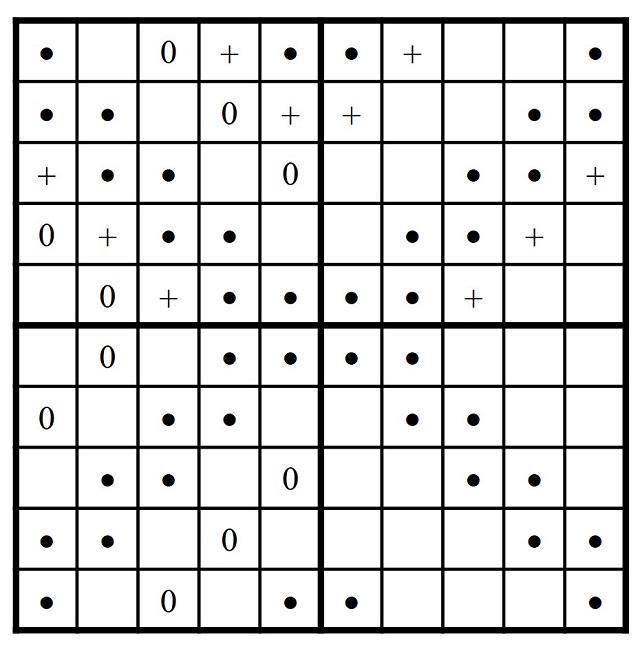
Después volvemos a contar, empezando en la esquina de arriba a la derecha y contando de derecha a izquierda y de arriba abajo, pero son los ceros las que utilizamos de guía para colocar los números. Y finalmente, se vuelve a hacer la operación en sentido contrario, desde la casilla de abajo a la izquierda, pero apoyándonos en las cruces. En la siguiente imagen vemos el caso del orden 6.

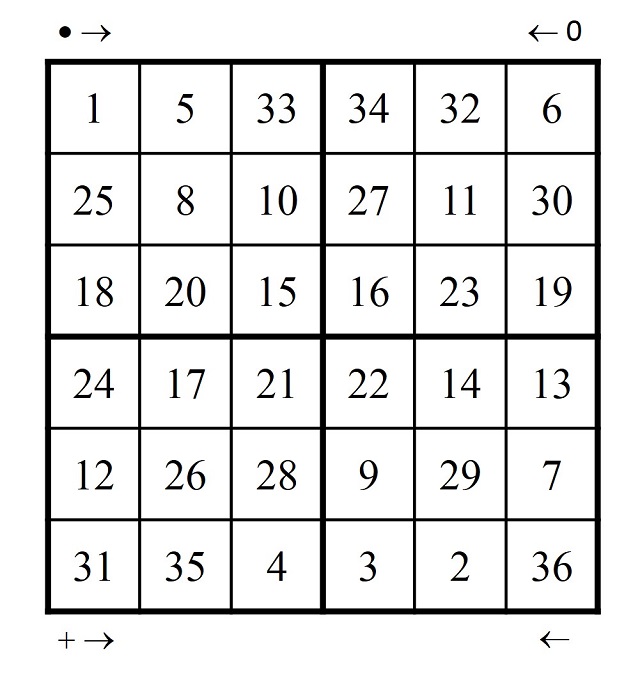
Estos son solo algunos de los muchos métodos, con un poco de historia, para construir cuadrados mágicos que existen.

Bibliografía:

1.- Jacques Sesiano, Magic Squares, Their History and Construction from Ancient Times to AD 1600, Springer, 2019.

2.- Jim Moran, The wonders of magic squares, Randon House Inc., 1982.

3.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

4.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Catarata, 2023 (pendiente de publicación).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica