Dibujando grafos sobre la banda de Moebius
La banda de Moebius es un sorprendente objeto geométrico, y más concretamente topológico (véase la entrada La topología modifica la trayectoria de los peces), que ha cautivado a personas de dentro y fuera de las matemáticas. En el Cuaderno de Cultura Científica hemos hablado en varias ocasiones, tanto de sus sorprendentes propiedades matemáticas, como de su utilización en el arte (algunas interesantes entradas sobre la misma son: Poesía retorcida sobre banda de Möbius, De menú para hoy, dos novelas gráficas negras con salsa matemática, Arte Moebius (I), Arte Moebius (II), En busca de la banda de Moebius más corta posible).

Podéis leer más sobre la banda de Moebius y su utilización en el arte contemporáneo en el libro Las matemáticas como herramienta de creación artística (R. Ibáñez, colección Miradas matemáticas, Catarata, 2023), que estará en las librerías a finales del mes de marzo.
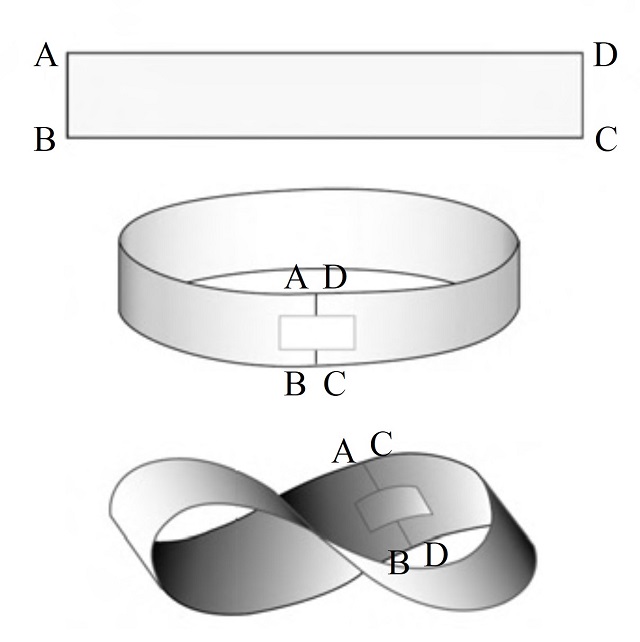
Pero en esta entrada del Cuaderno de Cultura Científica queremos hablar de una curiosa propiedad de la banda de Moebius, que tiene que ver con la teoría de grafos. Aunque esta superficie es un objeto matemático de sobra conocido, no está de más volver a recordar su construcción. Una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras y dos bordes, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde (como se observa en la siguiente imagen).
Por otra parte, la teoría de grafos es la rama de las matemáticas que estudia los grafos, estructuras formadas por puntos –llamados vértices– y líneas uniendo pares de puntos –llamadas aristas–, que son estructuras matemáticas muy sencillas, pero a la vez muy versátiles, con muchas aplicaciones en ciencia y tecnología (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (Gray) o El juego de Sim, entre otros).
Antes de adentrarnos en la mencionada propiedad de los grafos sobre la banda de Moebius, primero vamos a plantear un sencillo problema sobre grafos en el plano.
Problema: ¿Cual es el mayor número de puntos (vértices) que puede unirse mediante líneas (aristas), sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas?
Si tomamos un trozo de papel y empezamos a pintar puntos y líneas uniendo esos puntos, es fácil ver que el problema es trivial para 2, 3 y 4 puntos del plano, como se muestra en la siguiente imagen.
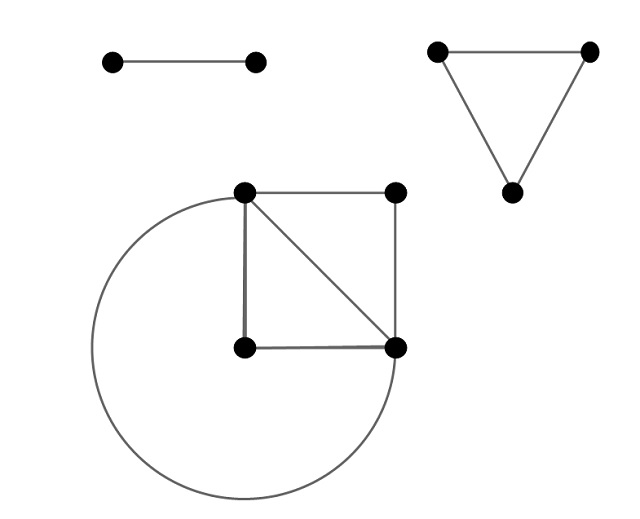
Pero parémonos a pensar un momento qué ocurre para 5 puntos. Empecemos dibujando el grafo de 5 puntos con todas las aristas posibles que unen dos de esos puntos, es lo que en matemáticas, en concreto, en teoría de grafos, se denomina el “grafo completo” de 5 vértices (y se denota como K5).
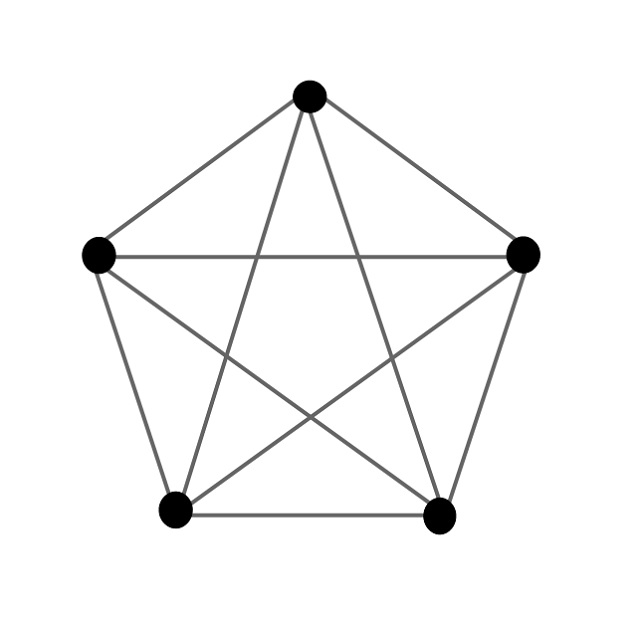
En el dibujo que hemos realizado del grafo completo de 5 vértices. Observamos que las aristas se cruzan entre ellas y nos planteamos si será posible redibujar las aristas de tal manera que estas no se crucen, como hemos visto que sí es posible para el grafo completo de 4 vértices, K4. Por cierto, esto es lo que en teoría de grafos se dice que es un “grafo plano”, un grafo que podemos dibujar en el plano sin que las aristas se crucen. Luego nuestro problema consiste en averiguar si el grafo completo de 5 vértices es plano, o no. La respuesta es negativa. Veamos una idea de cómo demostrarlo.
Para probar que el grafo completo de 5 vértices no es plano se hace uso de la fórmula de Euler. Esta establece que para los grafos planos “conexos” (esto quiere decir que cada par de vértices está conectado por un camino de aristas que empieza y termina en esos dos vértices) con v vértices, a aristas y c caras (se incluye también como cara la zona exterior no acotada) se verifica la fórmula:
![]()
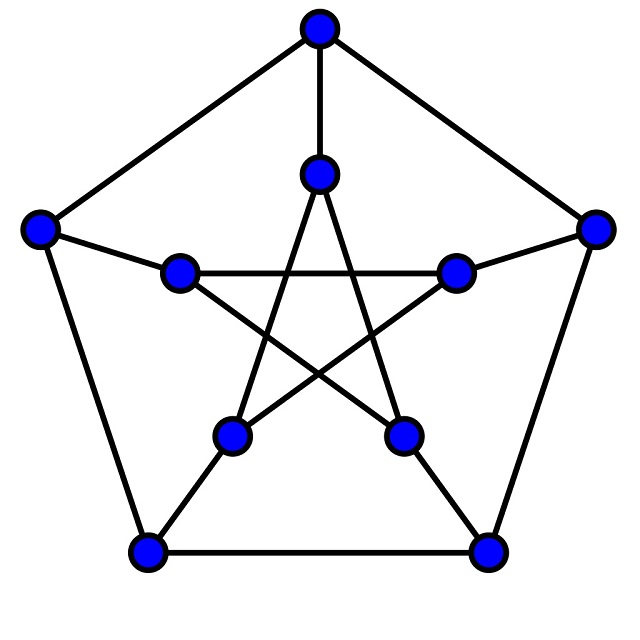
Por ejemplo, el grafo de Goldner-Harary, que vemos en la siguiente imagen, es un grafo plano y se verifica la fórmula de Euler (v = 11, a = 27 y c = 17).
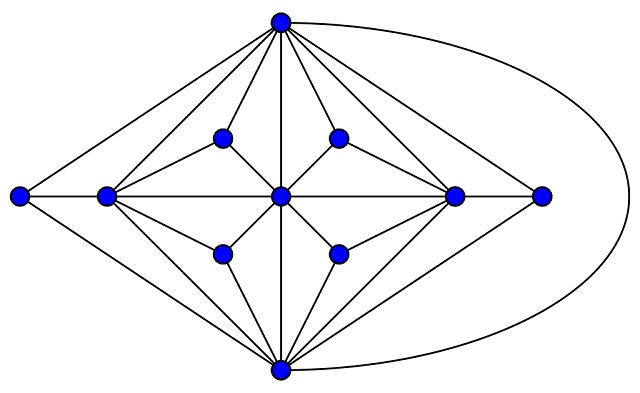
Ahora, si tenemos un grafo plano y simple (esto quiere decir que en ese grafo no hay bucles, es decir, aristas que unan un vértice consigo mismo, ni tampoco hay aristas múltiples, esto es, que no hay dos aristas distintas que unan los mismos dos vértices) con más de dos vértices, la fórmula de Euler permite afirmar (la prueba es simple) que
![]()
A partir de esta fórmula se demuestra que el grafo completo de 5 vértices no es plano, ya que v = 5, pero el número de aristas, al ser completo, es a = 10, y no se verifica la anterior desigualdad. Por lo tanto, queda demostrado que el grafo completo de 5 vértices K5 no es plano.
¿Pero qué ocurre si consideramos el problema sobre la banda de Moebius?
Problema: Dados 5 puntos en la banda de Moebius, ¿pueden unirse mediante líneas, sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas? ¿Es el grafo completo de 5 vértices sobre la banda de Moebius un “grafo plano”, es decir, cuyas aristas pueden trazarse de forma que no se crucen?
Antes de abordar esta cuestión, una pequeña reflexión sobre el concepto de superficie, ya que la banda de Moebius es una superficie (matemáticamente hablando). Esto es algo trivial, a priori, pero para entender bien este concepto, lo primero que hay que comprender es que una superficie matemática “ideal” no tiene grosor, luego sus puntos están “dentro” de la misma, no “sobre” ella. Para visualizar esto pensemos en una superficie transparente (por ejemplo, acetato) sobre la que se pinta un punto, este podrá verse “desde los dos lados”, lo cual nos permite entender qué significa que el punto está en la superficie, pero no sobre uno de sus lados. De hecho, podríamos decir que la superficie matemática no tiene “lados” en sí misma, sino que estos son una manifestación de la relación de la superficie con el espacio tridimensional que la contiene. En conclusión, a la hora de resolver el problema anterior sobre la banda de Moebius, es conveniente que pensemos en la banda de Moebius como si fuese una superficie transparente sobre la que pintamos las aristas.
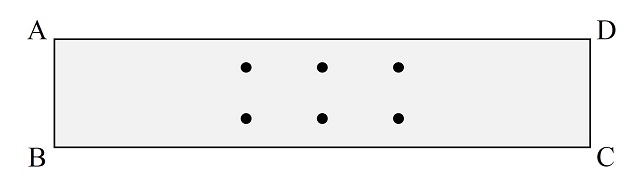
Ahora, contrariamente a lo que ocurría para el plano, dados 5 puntos en la banda de Moebius sí se pueden trazar líneas que unan todas las parejas de puntos sin que se crucen entre ellas, como se muestra en la siguiente imagen (se realiza el dibujo sobre la tira de papel estirada, teniendo en cuenta que luego los extremos se unen después de medio giro, por eso la línea que pasa por y en el lado AB, arriba a la izquierda, continua por abajo a la derecha en el lado CD).
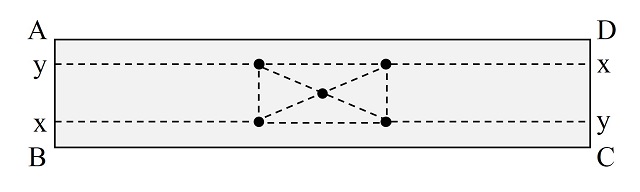
El siguiente paso sería ver si es posible lo mismo para 6 puntos, es decir, si el grafo completo de 6 vértices es un grafo “plano” en la banda de Moebius.
Problema: Dados 6 puntos en la banda de Moebius, ¿pueden unirse mediante líneas, sin que estas se crucen unas con otras y de manera que todos los pares de puntos queden unidos por líneas?
Este problema queda para quienes queráis divertiros intentando resolverlo. No olvidéis que estáis sobre una banda de Moebius, es decir, una tira de papel cuyos extremos se unen después de dar media vuelta a la misma. ¡Que os divirtáis!
El problema anterior está relacionado con un pasatiempo matemático clásico, el problema del agua, el gas y la electricidad, también conocido como problema de los tres servicios. Este problema aparece recogido en el libro Amusements in mathematics (1917), que fue publicado en castellano en tres partes, con el nombre conjunto de Diversiones Matemáticas (El acertijo del mandarín, Los gatos del hechicero y El misterio del muelle), del experto inglés en matemática recreativa Henry E. Dudeney (1857-1930). Aunque ya lo había publicado con anterioridad, en 1913, en la revista The Strand Magazine. Dudeney dice que es un pasatiempo matemático muy antiguo, que él ha bautizado como el problema del agua, el gas y la electricidad, aunque es más antiguo que la utilización de la electricidad para iluminar las casas. El problema, traducido del original de Dudeney, dice así.
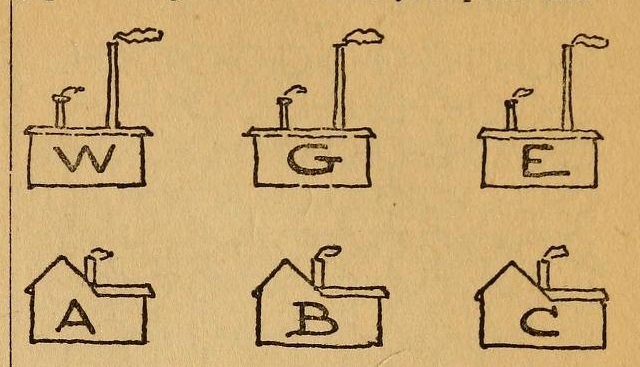
El problema del agua, el gas y la electricidad: El rompecabezas consiste en tender agua, gas y electricidad, desde W, G y E, a cada una de las tres casas, A, B y C, sin que ninguna tubería se cruce con otra. Coge tu lápiz y dibuja líneas que muestren cómo hacerlo. Pronto te encontrarás con dificultades.
Según vayáis intentando resolver este problema clásico os daréis cuenta de que nos encontramos ante una cuestión similar a la anterior, que era intentar dibujar el grafo completo K5 de 5 vértices sin que se crucen las líneas. Sin embargo, ahora el grafo asociado al problema del agua, el gas y la electricidad, que es el grafo bipartito completo K3,3 (que aparece en la siguiente imagen), es decir, está formado por dos conjuntos de vértices, en este caso, de 3 vértices cada uno, y están todas las aristas que unen los vértices de un conjunto con los del otro.
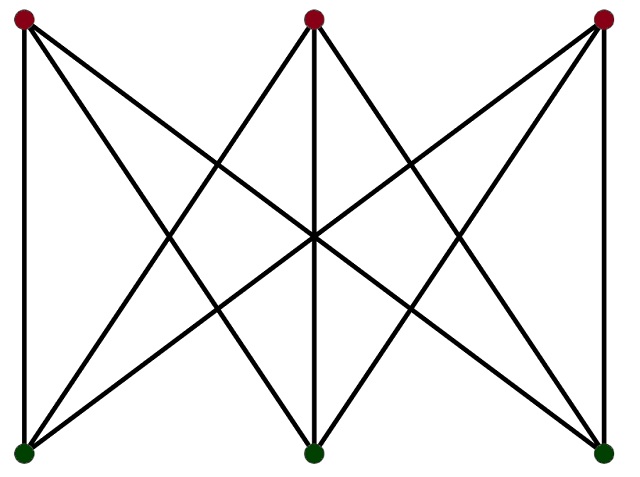
Utilizando de nuevo la fórmula que es consecuencia de la fórmula de Euler puede demostrarse que el grafo bipartito completo K3,3 no es plano y el problema del agua, el gas y la electricidad no tiene solución.
Para terminar…
Problema: ¿es posible resolver el problema del agua, el gas y la electricidad para la banda de Moebius?

Bibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística , colección Miradas matemáticas, Catarata, 2023.
2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.
3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.
4.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
5.- David E. Kullman, The utilities problem, Mathematics Magazine, 52 (5), pp. 299–302, 1979.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica