«No me imagino una vida más plena que una vida dedicada a la matemática»

Augustin Louis Cauchy

Augustin Louis Cauchy (1789-1857) fue un matemático francés, uno de los más prolíficos de todos los tiempos en esta disciplina científica. Investigó en todas las áreas matemáticas de su época, siendo pionero en análisis; entre otros, introdujo las funciones holomorfas, los criterios de convergencia de series y las series de potencias.

En 1840, en la nota Sur les moyens d’éviter les erreurs de calculs numériques (Sobre la manera de evitar errores de cálculo numérico) publicada en los Comptes-Rendus de l’Académie des Sciences, Cauchy proponía una manera diferente de escribir los números usando dos tipos de dígitos, uno positivo y el otro negativo.

Imaginemos que, en un número escrito en cifras, se coloca el signo sobre la cifra correspondiente a las unidades de cierto orden para expresar que las unidades de ese orden deben tomarse efectivamente con el signo −. Podremos distinguir en cada número dos especies de cifras, algunas positivas, y las otras negativas. […] Con este planteamiento, obviamente podremos escribir cualquier número con dígitos cuyo valor numérico sea como máximo igual a 5.

En esta nueva notación propuesta por Cauchy, los números del 1 al 20 pueden escribirse como se indica en la siguiente tabla:

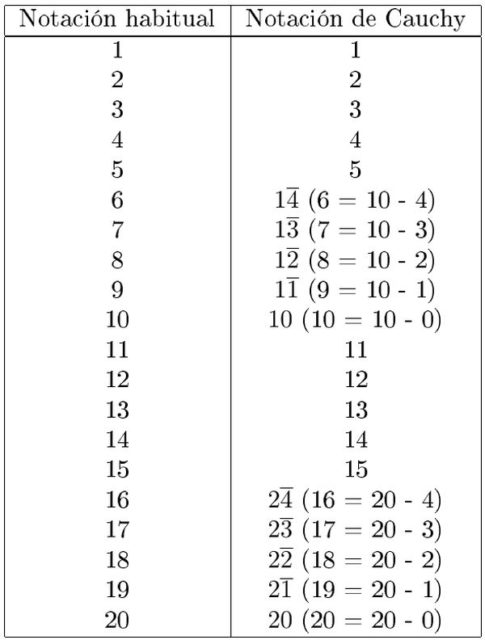
La escritura de un número con la notación de Cauchy no es única. Por ejemplo, el número 55 puede escribirse de estas tres maneras diferentes:

Para encontrar el opuesto de un número con la notación de Cauchy, basta con poner una barra sobre los números que no la tenían y eliminarla de aquellos que sí la llevaban (se cambia el signo de las operaciones indicadas en la escritura de Cauchy, al ser la suma de un número y su opuesto igual a 0).

Sumando números con la notación de Cauchy

Sumar no es difícil con la notación propuesta por el matemático francés. Debajo se muestra una tabla de sumar.

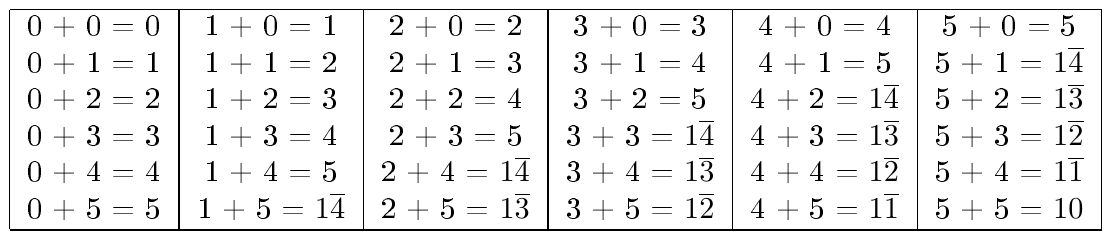
Restar dos números consiste en sumar al minuendo el opuesto del sustraendo. Como ya sabemos la manera de calcular el opuesto de un número con la notación de Cauchy, basta con entender y aplicar las reglas de la suma.

Cambio de una forma de numeración a la otra

Para pasar de la notación usual a la notación de Cauchy basta con sustituir en el número dado cada secuencia continua de cifras positivas mayores que 4 por cifras negativas que forman, en valor absoluto, el complemento aritmético de esta sucesión, y añadir a la cifra que la precede una unidad. Si el último dígito de la secuencia es 5, podríamos ignorarlo y excluirlo de ella. Se muestra un ejemplo debajo (los números en la notación usual están en negro y con la notación de Cauchy en rojo para entender mejor la operación):

Inversamente, para transformar un número con la notación de Cauchy en un número con la notación estándar, basta con reemplazar cada secuencia continua de números negativos por el complementario aritmético de esta secuencia, y disminuir en una unidad la cifra positiva que le precede. Se muestra un ejemplo debajo:

La multiplicación con la notación de Cauchy

En su artículo, Cauchy explica que, como con su notación las cifras no sobrepasan el 5, la tabla de multiplicar puede reducirse a la cuarta parte de su extensión habitual, y basta con efectuar multiplicaciones parciales por 2, 3, 4 = 2 x 2 y 5 = 10/2. El matemático recuerda, además, que el producto de dos cifras de la misma especie (ambas positivas o ambas negativas) es siempre positivo, mientras que el producto de dos cifras de distinta especie (uno positivo y otro negativo) será negativo. Así, se obtiene de este modo una sencilla tabla de multiplicar.

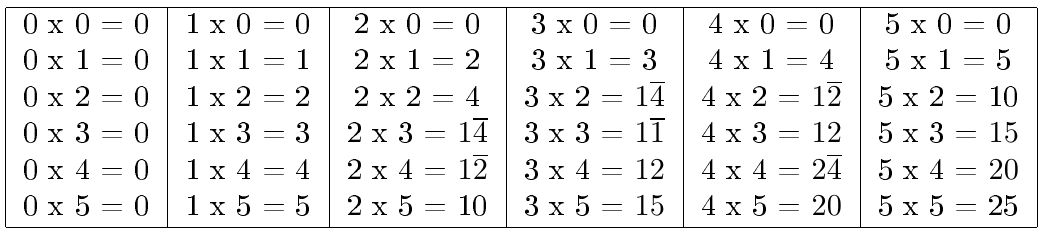
Dos números se multiplican de la misma manera en la que lo hacemos con la notación habitual, y usando las tablas de sumar y multiplicar que se han introducido antes. Para la división, de nuevo, basta con actuar como tenemos costumbre, con las nuevas reglas aprendidas.

¿Por qué esta notación?

Cauchy no pretendía sustituir el método clásico de numeración por el suyo, proponía usarlos en paralelo. Comentaba, de hecho, en su nota en los Comptes-Rendus de l’Académie des Sciences:

[…] Para poder ofrecer el resultado de un cálculo como digno de ser adoptado con confianza, lo que debe hacerse no es repetir el mismo cálculo dos veces siguiendo la misma ruta, dado que es bastante natural que uno vuelva a caer en un error ya cometido. Por el contrario, es determinar todo de tal manera que, por medio de dos sistemas de operaciones muy distintos, lleguemos de nuevo a resultados idénticos.

Referencias

• Gérard Grancher, Compter comme Cauchy ou diviser par 4 la taille des tables de multiplication, Café des maths, Images des mathématiques, 14 de agosto de 2020

• Augustin Louis Cauchy (1840). Sur les moyens d’éviter les erreurs de calculs numériques, Comptes-Rendus de l’Académie des Sciences 11, 789-798, 826 [en Gallica, Œuvres complètes, série 1, tome 5, 431-442].

Para saber más:
De la grandeur a las matemáticas puras

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad