En la anterior entrada del Cuaderno de Cultura Científica, titulada Sucesiones fractales, analizamos las sucesiones infinitas de números enteros denominadas autosemejantes, o fractales, que imitan la propiedad de autosemejanza de los objetos fractales. En concreto, una sucesión (infinita) de números enteros se dice que es una sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Por ejemplo, tomemos la sucesión
1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 2, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 2, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 2, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 2, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 2, 1, 0, 0, 1, 0, 1, 0, …
que es la sucesión A000161 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, y que se define de la siguiente manera: para cada posición n de la sucesión (empezando en 0), el número que está en dicha posición es igual a la cantidad de formas de expresar n como suma de dos cuadrados (es posible que no haya ninguna), sin importar el orden. Así, teniendo en cuenta que los primeros cuadrados son 0, 1, 4, 9, 16, 25, etc, se tiene que 0 se puede expresar como 0 + 0; 1 se puede expresar como 0 + 1; 2 como 1 + 1; 3 no se puede expresar como suma de cuadrados; 4 es igual a 4 + 0; 5 es igual a 4 + 1; 6 y 7 no se pueden expresar como suma de cuadrados; 8 se puede expresar como 4 + 4; 9 como 9 + 0; 10 es igual a 9 + 1; 11 y 12 no se pueden expresar como suma de cuadrados; 13 como 9 + 4; y así seguiríamos con el resto. La primera vez que aparece el 2 es para n = 25, ya que 25 = 25 + 0 = 16 + 9, o la primera vez que aparece el 3 en la sucesión es para n = 325, ya que 325 = 324 + 1 = 289 + 36 = 225 + 100.
Esta sucesión es una sucesión fractal ya que si eliminamos los números que están en las posiciones impares (cuidado, ya que estamos empezando en n = 0), es decir, nos quedamos con los números que están en las posiciones pares, esta sigue siendo la sucesión original, como se puede comprobar arriba para los primeros términos.
¿Qué es la sucesión de Thue-Morse?
En esta entrada vamos a centrarnos en una sucesión fractal concreta, conocida con el nombre de sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas, como puede leerse en el artículo The ubiquitous Prouhet-Thue-Morse sequence (La omnipresente sucesión de Prouhet-Thue-Morse) de Jean-Paul Allouche y Jeffrey Shallit, desde la combinatoria de palabras a problemas de ajedrez, pasando por la geometría diferencial, la teoría de números, el análisis matemático de funciones, la física matemática, los cuasi-cristales o la teoría de grupos.
Empecemos definiendo esta sucesión. La sucesión de Thue-Morse es una sucesión infinita (la sucesión A010060 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) cuyos elementos son ceros y unos y que se define recursivamente de la siguiente manera. Si la denotamos como {tn}, entonces t0 = 0 y t2n = tn, t2n + 1 = 1 – tn. Por lo tanto, los primeros términos de la sucesión, como podéis calcular desde la definición, son:
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
Otra manera de definir esta sucesión es utilizando las representaciones binarias de los números. Se empieza representando los números, desde n = 0, en base 2, como aparece en la siguiente imagen (de hecho, esto ya lo hicimos para la entrada Sucesiones fractales).

La sucesión de Thue-Morse se obtiene sumando, para cada número n, los unos (1) que aparecen en su representación binaria, si es una cantidad par se considera el número 0 y si es impar el número 1 (matemáticamente podemos decir que es la suma de los dígitos de su representación binaria, módulo 2). Por ejemplo, 29 se representa como 11101, que tiene una cantidad par de unos, luego para n = 29 se toma el valor 0 en la sucesión (t29 = 0), mientras que para n = 37 se toma el valor 1 ya que 37 se representa en base dos como 100101 (t37 = 1). Luego, para los primeros números n (los de la imagen anterior) se obtienen los primeros términos de esta sucesión binaria: 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1.
En la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), de los matemáticos John H. Conway, Richard K. Guy y Elwyn Berlekamp, se denominan números malvados (evil numbers en inglés) a aquellos números tales que su representación binaria tiene un número par de unos, es decir, se corresponden con los ceros de la sucesión de Thue-Morse, que, como se observa en la imagen anterior, serían 0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, etc. Por otra parte, se llaman números odiosos a aquellos con una cantidad impar de unos en su representación binaria, es decir, que se corresponden con los unos de la sucesión de Thue-Morse, que son 1, 2, 4, 7, 8, 11, 13, 14, 16, 19, 21, 22, 25, 26, 28, 31, 32, 35, 37, 38, etc.
Una tercera forma de definir la sucesión de Thue-Morse es utilizando, de manera recursiva, el complemento, o negación, bit a bit (dígito a dígito) de un número binario. Empecemos definiendo qué es el complemento, o negación, bit a bit (dígito a dígito) de un número binario: esta operación consiste en cambiar cada dígito de una representación binaria por su complemento, es decir, si es un 1 se cambia por 0, y si es un 0 se cambia por 1. Por ejemplo, el complemento del número binario 100100110 será C[100100110] = 011011001.
Para definir la sucesión de Thue-Morse se realizan los siguientes pasos. Se empieza por T(0) = 0 y en casa paso se toma el número binario del paso anterior seguido de su complemento bit a bit, esto es, T(k + 1) = T(k)C[T(k)]. Así, los primeros pasos serían:
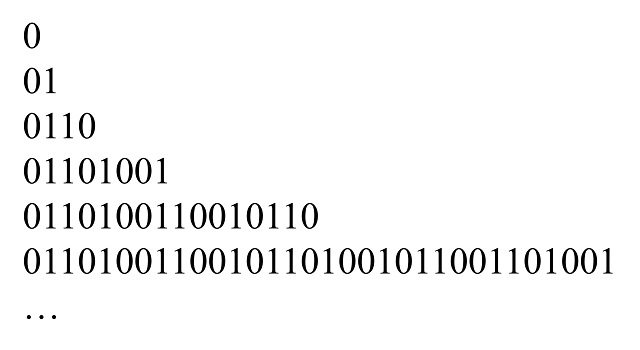
La sucesión de Thue-Morse se obtendría siguiendo este proceso hasta el infinito, T(infinito).
Una curiosidad de esta definición es que en los pasos pares T(2k) se obtienen números binarios capicúas, 0, 0110, 0110100110010110, etc.
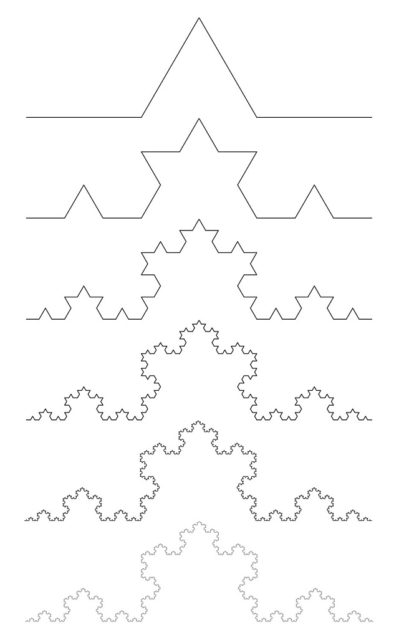
Una forma similar de construir la sucesión de Thue-Morse mediante una serie de transformaciones consiste en empezar en 0 y luego en cada paso transformar 0 en 01 y 1 en 10. Así, como se empieza en 0, en el primer paso 0 se transforma en 01; en el segundo paso, al trasformar los dos dígitos de 10, mediante la transformación descrita, quedaría 0110; el siguiente paso da como resultado 01101001; el siguiente 0110100110010110; y vemos que vamos obteniendo los mismos términos que en la descripción anterior.
El origen de la sucesión de Thue-Morse
A principios del siglo XX el matemático noruego Axel Thue (1863-1922), en dos artículos publicados en 1906 y 1912 (que supusieron el origen de una rama de la combinatoria denominada combinatoria de palabras), se planteó el problema de construir sucesiones sobre alfabetos finitos (un alfabeto es un conjunto finito de símbolos (letras), por ejemplo, un alfabeto binario consta de dos símbolos, como los símbolos 0 y 1, o cualquier otro par de símbolos; y el alfabeto del español tiene 27 letras) libres de cuadrados o de cubos.
Una sucesión se dice que está libre de cuadrados si no es posible tomar un conjunto de elementos consecutivos de la sucesión que formen una “palabra” (es decir, una sucesión de símbolos, por ejemplo, “1001001” es una palabra en el alfabeto binario y “abracadabra” o “prgtrro” son palabras en el alfabeto de 27 letras, aunque la segunda no tiene significado alguno) de la forma WW, donde W es una palabra no vacía. Por ejemplo, la palabra binaria anterior no está libre de cuadrados, ya que contiene la palabra “00”, que es un cuadrado tomando W = “0”, o también contiene el cuadrado “001001” para W = “001”. De forma similar se definen las palabras libres de cubos, cuando no contiene una palabra de la forma WWW.
Axel Thue observó que toda sucesión binaria con al menos 4 elementos contiene cuadrados, luego no existen sucesiones infinitas binarias libres de cuadrados. Entonces se planteó algunas cuestiones relacionadas como la existencia de sucesiones infinitas con tres letras libres de cuadrados o la existencia de sucesiones binarias infinitas libres de cubos, o de solapamientos (esto es, palabras de la forma vWvWv, donde W es una palabra y v es una letra de este alfabeto binario, es decir, 0 o 1). La respuesta a esas cuestiones venía de la mano de la sucesión que lleva su nombre.
La demostración de que toda sucesión binaria con más de 4 elementos contiene cuadrados es bastante sencilla. Veámosla. Si la sucesión binaria empezase por 0 (el argumento es similar si empezamos por 1), el siguiente término de la sucesión debería ser 1, ya que si fuese 0 tendríamos un cuadrado “00”. Luego los dos primeros términos de la sucesión serían {0, 1} (si hubiésemos empezado por 1 serían {1, 0}). De la misma manera, el tercer término deberá ser 0, ya que si fuese 1, de nuevo tendríamos un cuadrado, en este caso “11”. Por lo tanto, los tres primeros términos de la sucesión libre de cuadrados serían {0, 1, 0} (si hubiésemos empezado por 1 serían {1, 0, 1}). Llegados a este punto, si el siguiente término de la sucesión es 0, la sucesión es {0, 1, 0, 0} y tenemos un cuadrado “00”, mientras que si el siguiente término es 1, la sucesión es {0, 1, 0, 1} y el cuadrado es “0101”. Así, queda demostrada la afirmación de Thue.
Un resultado que puede verse en la literatura (puede leerse alguna de las demostraciones de este resultado en algunos de los textos de la bibliografía, como el capítulo Substitutions and symbolic dynamical systems) es que la sucesión de Thue-Morse no contiene palabras de la forma WWv, donde W es una palabra no vacía (es decir, con alguna letra) y v es la primera letra de la palabra W. Como consecuencia (corolario) de este resultado se tiene:
A. La sucesión de Thue-Morse es una sucesión binaria infinita no periódica, es decir, no existe una palabra finita W que genere, por repetición, toda la sucesión infinita (por ejemplo, entre los ejemplos de sucesiones autosemejantes de la entrada Sucesiones fractales se incluía la sucesión 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … que es una sucesión periódica de periodo W = 1, 2, 2, 3, 2, 3, 3), ya que si existiese un periodo W tendríamos que existiría una palabra de la forma Wwv, con v la primera letra de la palabra W, lo cual no es posible por el resultado anterior;
B. La sucesión de Thue-Morse es una sucesión binaria infinita que no admite cubos (WWW), ni solapamientos (vWvWv), dando respuesta a dos de las cuestiones de Thue.
Además, la sucesión de Prouhet-Thue-Morse permite construir una sucesión infinita sobre un alfabeto de tres letras libre de cubos. Se define la sucesión vn , para n mayor o igual que 1, de la siguiente manera, vn es igual a la cantidad de unos (1) que hay entre el cero (0) que está en la posición n-ésima y en cero (0) que está en la posición (n + 1)-ésima. Como la sucesión de Thue-Morse empieza
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
entonces la nueva sucesión sería, según la definición,
2, 1, 0, 2, 0, 1, 2, 1, 0, 1, 2, 0, 2, 1, 0, 2, 0, 1, 2, 0, 2, 1, 0, 1, 2, 1, 0, 2, 0, 1, 2, 1, 0, 1, 2, 0, 2, 1, 0, 1, 2, 1, 0, 2, 0, 1, 2, 0, 2, 1, 0, 2, …
Utilizando que la sucesión original no admite solapamientos (vWvWv) puede probarse que la sucesión descrita anteriormente es una sucesión infinita sobre un alfabeto de tres letras {0, 1, 2} y que está libre de cuadrados.
Los artículos del matemático noruego Axel Thue fueron publicados en una revista noruega y pasaron desapercibidos durante mucho tiempo, motivo por el cual esta sucesión fue redescubierta por otras personas. Por ejemplo, el matemático estadounidense Harold Marston Morse (1892-1977) redescubrió la sucesión binaria infinita 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, … en relación con una investigación en el campo de la geometría diferencial, e concreto, sobre superficies de curvatura negativa.
Posteriormente se conocería que esta sucesión ya aparecía, de forma implícita, en un artículo de 1851 del matemático francés Eugène Prouhet (1817-1867) en relación con un problema de teoría de números.
El problema del juego infinito en el ajedrez
El matemático y jugador de ajedrez neerlandés Machgielis (Max) Euwe (1901-1981), que fuera campeón del mundo de ajedrez en 1935 y profesor de matemáticas en las universidades de Róterdam y Tilburg, también redescubrió, de forma independiente, la sucesión de Thue-Morse en relación con el ajedrez.
Una de las reglas del ajedrez (conocida como regla alemana) decía que si en una partida de ajedrez se repetía tres veces, de forma consecutiva, una misma secuencia de movimientos, se consideraba que el juego terminaba en tablas. Euwe demostró, en un artículo de 1929, que podía realizarse una partida de ajedrez infinita evitando la regla alemana, es decir, que una misma secuencia de movimientos se repitiera tres veces consecutivas. Para ello consideró una secuencia de cuatro movimientos, que se corresponde con el 0, y una secuencia de otros cuatro movimientos, que se corresponde con el 1, y se inventó una sucesión binaria infinita libre de cubos, para evitar la regla alemana, que no es otra que la sucesión de Thue-Morse, aunque el ajedrecista y matemático desconocía la existencia de la misma.
Por este motivo se introdujeron dos reglas más fuertes para declarar tablas en un juego y evitar el juego infinito, la regla de la triple repetición y la regla de los cincuenta movimientos. De hecho, la regla de la triple repetición establece que la partida ha terminado en tablas si se repite tres veces una misma secuencia de movimientos, aunque no sea de forma consecutiva,

Bibliografía
1.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
2.- Jean-Paul Allouche, Jeffrey Shallit, The ubiquitous Prouhet-Thue-Morse sequence, incluido en el libro Sequences and their Applications, Springer, 1999.
3.- Christopher Williamson, An Overview of the Thue-Morse Sequence (manuscrito no publicado). University of Washington, 2012.
4.- S. Ferenczi, Substitutions and symbolic dynamical systems (capítulo), Substitutions in Dynamics, Arithmetics and Combinatorics, Springer, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
La sucesión fractal de Thue-Morse y la p…
[…] La sucesión de Thue-Morse aparece en diferentes ramas de las matemáticas, desde la combinatoria a la física matemátic o la teoría de grupos. […]
Ion (Flamarique Estanga)
Hola, el tablero de ajedrez de la última imagen del artículo (muy interesante por cierto) cuyo pie de foto titula : “Juego de piezas abstractas de ajedrez …”, está mal colocado. La torre negra en primer término tiene que estar en un cuadrado blanco, como la torre blanca de arriba, más cercana al rey blanco. Error de principiantes o de ignorantes en ajedrez.