Mi libro La gran familia de los números (2021), de la colección Miradas matemáticas (Catarata, ICMAT, FESPM), está dedicado a algunas importantes familias de números naturales, entre los que están los números figurados, primos, capicúas, cíclicos, perfectos, amigos, intocables, narcisistas, felices o vampiros, entre muchos otros.

Por sus dígitos los conoceréis

En el capítulo 5, titulado “Por sus dígitos los conoceréis”, se muestran familias de números naturales definidas por características de los dígitos de sus representaciones numéricas, como los números narcisistas (sobre los que también podéis leer en la entrada ¿Pueden los números enamorarse de su propia imagen?), que son aquellos números que son iguales a la suma de las potencias de sus dígitos elevados a la cantidad de dígitos que tiene el número. Por ejemplo, el número 153 es un número narcisista, puesto que, teniendo 3 cifras, que son 1, 5 y 3, se cumple que 1³ + 5³ + 3³ = 1 + 125 + 27 = 153; o también, el número 1.634, ya que 1⁴ + 6⁴ + 3⁴ + 4⁴ = 1 + 1.296 + 81 + 256 = 1.634.

Otra familia de números relacionada con los números narcisistas es la que podríamos llamar números de Follet, puesto que aparecen mencionados en la novela Doble juego (2000), del escritor Ken Follet, que está formada por aquellos números que son iguales a la suma de las potencias de sus dígitos elevados a la posición que ocupan en el número (empezando por la izquierda), como el número 175, ya que 1¹ + 7² + 5³ = 175 (1 es el primer dígito, 7 el segundo y 5 el tercero).

Otra familia de números relacionada con los números narcisistas es la formada por los números de Munchausen, aquellos números que son iguales a la suma de sus dígitos elevados a ellos mismos. Por ejemplo, el número 3.435 es un número de Munchausen, ya que 3³ + 4⁴ + 3³ + 5⁵ = 3.435 (si admitimos que 0⁰ = 1, resulta que el anterior número es el único que existe).

Una extensión natural de los números narcisistas es considerar que los dígitos están elevados, no a la cantidad de dígitos del número, sino a una cifra fija cualquiera, llamada orden. En este caso, a los números que son iguales a la suma de las potencias de sus dígitos elevados a una cantidad fija cualquiera, no necesariamente la cantidad de dígitos del número, se les llama números potentes o también invariantes digitales perfectos. Por ejemplo, el número 4.150, que puede expresarse como la suma de las potencias quintas de sus dígitos (que son solo cuatro), 4⁵ + 1⁵ + 5⁵ + 0⁵ = 1.024 + 1 + 3.125 = 4.150, es un número potente. Los números insólitos están relacionados con estos últimos.

Los números insólitos

En el artículo On a very thin sequence of integers (Sobre una sucesión de números enteros poco numerosa), sus autores introducen el término de número insólito. Definen un número insólito como aquel número, mayor que 1, para el cual la suma y el producto de las potencias cuadradas de sus dígitos divide al propio número (en particular, no contiene al 0 entre sus dígitos). Por ejemplo, dado el número 122.121.216, la suma de los cuadrados de sus dígitos es

1² + 2² + 2² + 1² + 2² + 1² + 2² + 1² + 6² = 56,

mientras el producto de los cuadrados de sus dígitos es

1² x 2² x 2² x 1² x 2² x 1² x 2² x 1² x 6² = 9.216,

y como ambos dividen a número 122.121.216, por lo tanto, es un número insólito.

El número más pequeño que es insólito es el 111, ya que es divisible por 3 (suma de los cuadrados de sus dígitos) y por 1 (producto de los cuadrados de sus dígitos). Y los diez primeros números insólitos son:

111, 11.112, 1.122.112, 111.111.111, 122.121.216, 1.111.112.112, 1.111.211.136, 1.116.122.112, 1.211.162.112 y 11.111.113.116.

La sucesión de números insólitos es la sucesión A098034 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS. Además, existen solo 428 números insólitos más pequeños que 100 trillones, 10²⁰ = 100.000.000.000.000.000.000.

En la siguiente tabla se muestran los primeros números insólitos que contienen una cifra concreta entre sus dígitos, del 1 al 9.

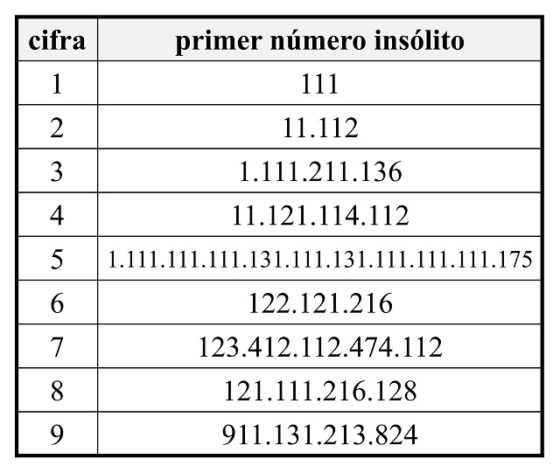
Parece ser que es muy difícil encontrar números insólitos que contengan la cifra 5. Como se muestra en la anterior tabla, el número insólito más pequeño que incluye la cifra 5 tiene 31 dígitos. Además, el siguiente número insólito que contiene a la cifra 5 tiene 37 dígitos:

1.111.111.111.111.111.117.111.111.111.911.111.375.

Por otra parte, el número insólito más pequeño que contiene todas las cifras, con la excepción del 5 teniendo en cuenta lo comentado, tiene 18 dígitos y es el siguiente:

711.813.411.914.121.216.

¿Existen infinitos números insólitos?

Si miramos a las familias de números naturales definidas por características de los dígitos de sus representaciones numéricas, que hemos comentado al inicio de esta entrada, tenemos que:

A. Existe una cantidad finita de números narcisistas (en el libro La gran familia de los números puede leerse una sencilla demostración de que no existen números narcisistas con más de 60 dígitos), concretamente, hay tan solo 88 números narcisistas;

B. solo existe una cantidad finita de números de Follet (también en el libro La gran familia de los números, puede leerse una sencilla demostración de que no existen números de Follet con más de 22 dígitos), en concreto, hay 19 números en esta familia;

C. tan solo hay un número de Munchausen, el 3.435 (asumiendo que 0⁰ = 1, aunque si se considera que 0⁰ = 0, o en la definición solo se consideran dígitos no nulos, entonces hay otro más, es el número 438.579.088);

D. se desconoce si la familia de invariantes digitales perfectos es finita o infinita.

Por lo tanto, podemos tener nuestras dudas sobre si existirá una cantidad finita o infinita de números insólitos.

A continuación, vamos a construir una familia de números insólitos, de lo cual se deducirá que existen infinitos números insólitos. Empecemos considerando los números repitunos (en inglés, repunit numbers), que son aquellos que están formados por la repetición de la cifra 1, es decir, 1, 11, 111, 1.111, 11.111, etc. Si consideramos un número repituno con k dígitos (todos ellos iguales a 1), entonces la suma de los cuadrados de sus dígitos es k y el producto de los cuadrados de sus dígitos es 1. Por lo tanto, un número repituno es un número insólito si el número de dígitos k divide al número. Por ejemplo, 111 es un número repituno que es insólito, puesto que 3 divide a 111 (recordemos la regla de divisibilidad del 3, que dice que un número es divisible por 3 si, y sólo si, la suma de sus dígitos es divisible por 3).

Teorema: Si k = 3ⁿ, entonces el número repituno con k dígitos es un número insólito.

Vamos a ver que efectivamente estos números repitunos son insólitos. Para n = 1 tenemos el número 111, que claramente es insólito, ya que 3 divide a 111.

Para n = 2, tenemos el número 111.111.111, que al dividirlo por 111 se obtiene 1.001.001:

Por lo tanto, el número 111.111.111 es divisible por 9 (que es la cantidad k = 3² de dígitos), ya que 111 es divisible por 3 y 1.001.001 también es divisible por 3 (sus dígitos suman 3).

Para n = 3, tenemos un número repituno formado por 27 unos, 111.111.111.111.111.111.111.111.111, que si lo dividimos por el anterior 111.111.111 (que es divisible por 9) se obtiene 1.000.000.001.000.000.001, es decir, 1 seguido de ocho 0, luego 1, otros ocho 0 y 1, que es divisible por 3. Por lo tanto, el número repituno con 27 = 3³ unos es un número insólito.

Y, de forma similar, se puede demostrar, por inducción, que los números repitunos con k = 3ⁿ son números insólitos.

Corolario: Existen infinitos números insólitos.

Los números insólitos son una curiosa familia de números naturales, de la que se conocen algunas propiedades matemáticas (algunas de ellas mostradas en esta entrada del Cuaderno de Cultura Científica) y de la que se seguirá investigando en el futuro, como ocurre con las demás familias, al menos para ampliar más nuestro conocimiento sobre la naturaleza de los números.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.

2.- J. M. De Koninck, N. Doyon, On a very thin sequence of integers, Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, tomo 20, pp. 157-177 (2001).

3.- Página web: Numbers Aplenty.

4.- Página web: Enciclopedia On-line de Sucesiones de Números Enteros – OEIS

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica