En mi anterior entrada del Cuaderno de Cultura Científica, titulada Los números insólitos, observábamos que había algunos números insólitos cuyos dígitos eran todos unos, en particular, 111 y 111.111.111, entre otros, los llamados números repitunos, a los que vamos a dedicar la entrada de hoy.

Los números repitunos

Empecemos por la definición.

Un número es un número repituno, en base b, si en la representación del número, en dicha base b, todos sus dígitos son unos (1).

Si empezamos con la base decimal (b = 10), que es la base que manejamos normalmente, tenemos que todo número repituno, como los números 11, 111, 1.111 o 11.111, que se representa (en base 10) con todo unos, puede expresarse de la forma

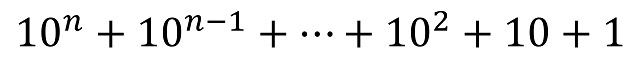
Y utilizando la fórmula de las progresiones geométricas, tenemos que los números repitunos (en base 10) son aquellos que pueden expresarse como

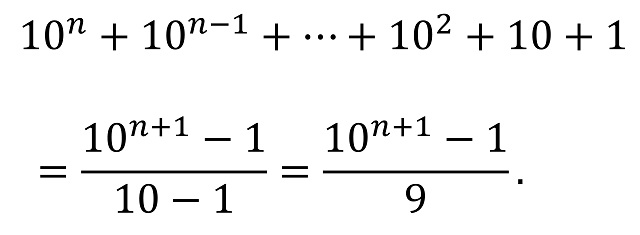
Por ejemplo, el número repituno 111.111 (para el cual n = 5) es igual a (10⁶ – 1) / 9 = (1.000.000 – 1) / 9 = 999.999 / 9 = 111.111.

En general, para cualquier base b se tiene que los números repitunos pueden expresarse de esta forma

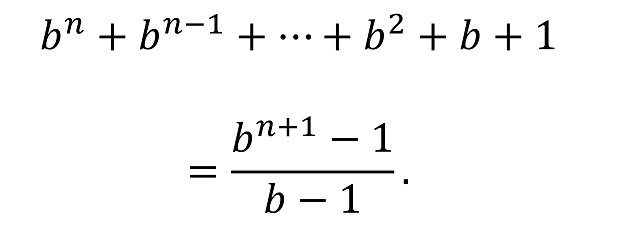
Si consideramos los números binarios (b = 2), cuyas cifras básicas son 0 y 1, tenemos que son, por la expresión anterior, los números de la forma 2^{n + 1} – 1, los llamados números de Mersenne (que reciben su nombre del sacerdote, filósofo, físico y matemático francés Marin Mersenne (1588-1648)). Los primeros números binarios repitunos serían (1)₂ = 1, (11)₂ = 2² – 1 = 3, (111)₂ = 2³ – 1 = 7, (1111)₂ = 2⁴ – 1 = 15, (11111)₂ = 2⁵ – 1 = 31 y (111111)₂ = 2⁶ – 1 = 63. Es decir, los números 1, 3, 7, 15, 31 y 63 son números repitunos en base 2.

Para los números ternarios (b = 3), cuyas cifras básicas son 0, 1 y 2, tenemos que son los números de la forma (3^{n + 1} – 1) / 2. Por lo tanto, los primeros números ternarios repitunos serían (1)₃ = 1, (11)₃ = (3² – 1) / 2 = 4, (111)₃ = (3³ – 1) / 2 = 13, (1111)₃ = (3⁴ – 1) / 2 = 40, (11111)₃ = (3⁵ – 1) / 2 = 121 y (111111)₃ = (3⁶ – 1) / 2 = 364, es decir, los números 1, 4, 13, 40, 121 y 364 son números repitunos en su representación en base 3.

Los números en base b = 4, o números cuaternarios, para los cuales las cifras básicas son 0, 1, 2 y 3, son repitunos si son de la forma (4^{n + 1} – 1) / 3. Los primeros números repitunos cuaternarios son entronces 1, 5, 21, 85, 341 y 1.365, ya que (1)₄ = 1, (11)₄ = (4² – 1) / 3 = 5, (111)₄ = (4³ – 1) / 3 = 21, (1111)₄ = (4⁴ – 1) / 3 = 85, (11111)₄ = (4⁵ – 1) / 3 = 341 y (111111)₄ = (4⁶ – 1) / 3 = 1.365.

En general, podemos hacer lo mismo para cualquier base b. Así, el número (1111)₇ = 400 es un número repituno en base 7 o el número (11111)₁₆ = 69.905 es un número repituno en base 16.

Si para cualquier base b tomamos n = 0 en la fórmula anterior tenemos que trivialmente el número 1 es un número repituno para cualquier base y si consideramos n = 1 se obtiene que b + 1 es un número repituno en la base b, ya que

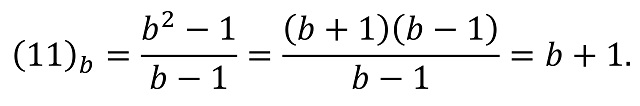
Es decir, dándole la vuelta al argumento anterior, todos los números naturales m son repitunos en alguna base, al menos, trivialmente, en la base m – 1.

El nombre de números repitunos, que en inglés se denominan “repunit”, viene de la expresión en inglés “repeated unit” (unidad repetida) y fue acuñada por el matemático Albert Beiler, en su libro Recreations in the Theory of Numbers: The Queen of Mathematics Entertains (1964).

Los números repitunos primos

Una cuestión que ha interesado dentro del estudio de los números repitunos, y que aparecía en el libro de Albert Beiler, es si son, o no, primos. Por ejemplo, el número 11 es un número repituno primo, pero no el número 111, ya que 111 = 3 x 37. Y, en general, se ha estudiado la factorización de los números repitunos.

A continuación, mostramos la factorización de los primeros números repitunos (en base decimal), a los cuales se les denota como R_k si están formados por k unos (a k se le suele llamar índice del número repituno).

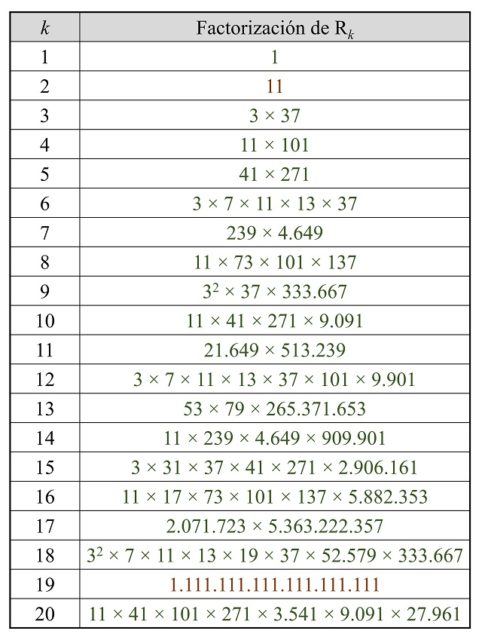
Entre los veinte primeros números repitunos solo hay dos que sean primos, que son R₂ = 11 y R₁₉ = 1.111.111.111.111.111.111. En general, la sucesión de la cantidad de unos (1) que tienen los números repitunos primos que se conocen a día de hoy, es decir, el índice de los mismos, es la sucesión A004023 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, cuyos términos son:

2, 19, 23, 317, 1.031, 49.081 (demostrado en marzo de 2.022), 86.453 (demostrado en mayo de 2023),

y se incluyen otros cuatro índices k tales que el número repituno R_k es probablemente primo, pero no está demostrado aún:

109.297, 270.343, 5.794.777, 8.177.207.

Como podemos observar, encontrar números repitunos primos es muy complicado. Mientras escribo esta entrada solo se conocen 7 repitunos primos y hay otros 4 que probablemente lo sean, pero aún no está demostrado.

Una primera criba sobre los índices de los números repitunos a la hora de buscar aquellos que sean primos es limitar la búsqueda a los índices primos ya que se puede probar que, si el índice k no es primo, tampoco lo es R_k. Vamos a demostrar esto, ya que es bastante sencillo, aunque puedes saltarte la demostración y seguir leyendo un poco más adelante.

Para demostrar la afirmación anterior vamos a hacer uso de la siguiente identidad algebraica, la fórmula de la diferencia de potencias:

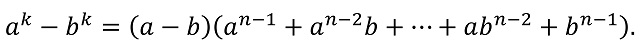
Ahora, supongamos que nuestro índice k no es primo, luego se puede expresar como un producto k = m x n, entonces vamos a probar que el número repituno R_k es divisible por los números repitunos R_m y R_n. De hecho, podemos expresarlo de la siguiente forma:

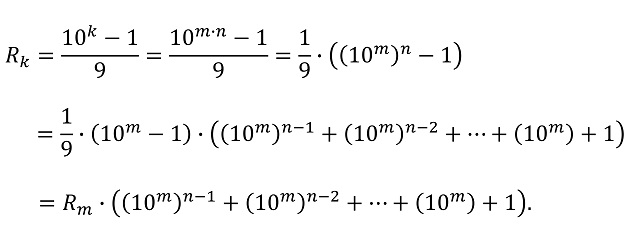
Luego R_m divide a R_k. De forma similar, se prueba que R_n también divide a R_k.

Por ejemplo, si k = 4 = 2², tenemos que R₂ = 11 divide a R₄ = 1.111 = 11 x 101, o si k = 6 = 2 x 3, el número repituno R₆ = 111.111 es divisible por R₂ = 11 y R₃ = 111 = 3 x 37.

También podríamos preguntarnos cuáles de los números repitunos en otras bases b son primos. Para empezar, de forma similar a como se ha demostrado antes, basta buscar entre los índices primos.

A los números repitunos binarios (b = 2), los números de Mersenne, es decir, de la forma 2^k – 1, que son primos se les llama números primos de Mersenne. Esta es una familia de números primos muy importante, en particular, en la búsqueda de números primos muy grandes. El número primo más grande que se conoce, encontrado en 2018, es el número primo de Mersenne

que tiene 24.862.048 dígitos (escrito en base decimal).

Los índices k para los cuales el número repituno binario con k unos (1), que es el número de Mersenne 2^k – 1, es primo es la sucesión A000043 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, cuyos primeros términos son

2, 3, 5, 7, 13, 17, 19, 31, 61, 89, …

Y los primos de Mersenne correspondientes forman la sucesión A000668, cuyos primeros términos son

3, 7, 31, 127, 8.191, 131.071, 524.287, 2.147.483.647, 2.305.843.009.213.693.951, 618.970.019.642.690.137.449.562.111, …

Se conocen nueve números repitunos ternarios primos, la sucesión A076481 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, cuyos dos primeros miembros son 13, que expresado en base ternaria es (111)₃, y 1.093, que se expresa en base ternaria como (1111111)₃.

Para la base b = 4 solo existe un número repituno primo, que es el número 5, es decir, (11)₄. Como hemos visto anteriormente, los números repitunos cuaternarios son de la forma (4^k – 1) / 3, pero podemos descomponer (4^k – 1) como producto de (2^k + 1) y (2^k – 1). Si tenemos en cuenta que (2^k + 1) es divisible por 3 para k impar y (2^k – 1) es divisible por 3 para k par, entonces todos los números repitunos cuaternarios, para k mayor que 2, son compuestos (no primos).

Y podríamos analizar también lo qué ocurre para las demás bases, pero dejemos esta cuestión y terminemos la entrada con un par de curiosidades sobre los números repitunos.

Algunas curiosidades de los números repitunos

Seguramente la propiedad más curiosa y conocida de los números repitunos es lo que ocurre cuando los elevamos al cuadrado. Si miramos a los nueve primeros cuadrados de los números repitunos (en la siguiente imagen) vemos que los resultados son una serie de números capicúas muy especiales, ya que están formados por los números naturales del 1 al k (para k desde 1 hasta 9), primero en orden creciente y después decreciente, puesto que son capicúas.

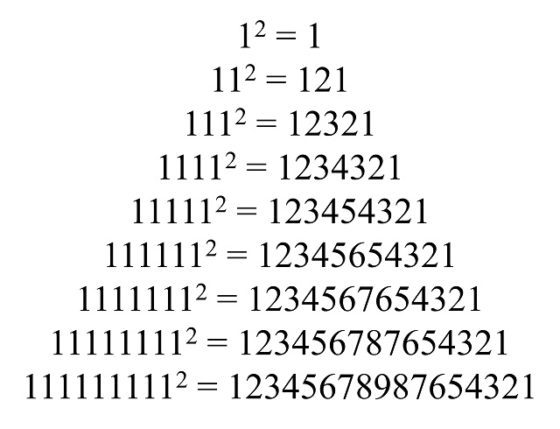
Sin embargo, a partir de k = 10 ya no obtenemos números capicúas, aunque sí se mantiene cierta simetría, como podemos apreciar en la siguiente imagen. Por ejemplo, cuando elevamos el número repituno de índice 10 al cuadrado, lo que queda es el número 1.234.567.900.987.654.321, que claramente no es capicúa. La primera parte, desde la izquierda, 1234567, se repite en sentido contrario en la derecha, 7654321, pero la parte de en medio no mantiene la simetría 900098. Si elevamos R₁₁ se obtiene 123.456.790.120.987.654.321.

Si observamos la siguiente imagen, que se corresponde con los números repitunos hasta índice 40, vemos que se mantiene cierta simetría. Por ejemplo, las cifras 2, 3, 4, 5, 6 y 7 están en posiciones simétricas, mientras que el 1 solo aparece en el lado izquierdo, a excepción de los extremos, y el 8 solo aparece en la derecha. Por otra parte, las cifras 0 y 9 mantienen cierta simetría.

Hemos obtenido números capicúas multiplicando R_k por R_k, para k entre 0 y 9, pero se pueden obtener otros números capicúas si se multiplica un número repunit R_m cualquiera por R_k, para k entre 0 y 9. Dejo como cuestión abierta analizar el resultado de tales multiplicaciones, que podéis analizar de forma progresiva sobre el índice k, empezando en k = 2.

Otra serie de expresiones curiosas para los primeros números repitunos es la siguiente:

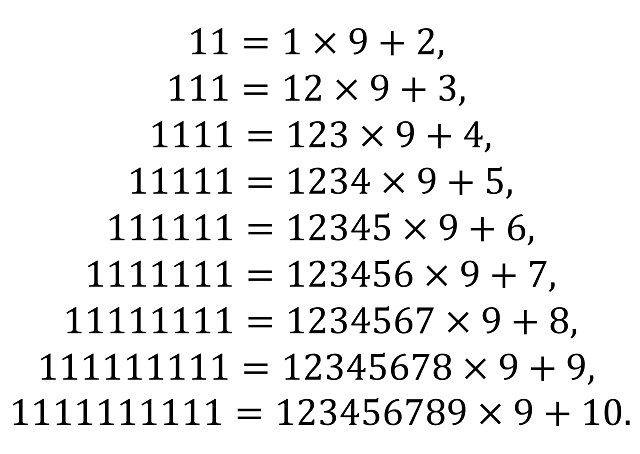
Nos podríamos plantear qué pasa para los demás números repitunos, aquellos con índice 11 o más. La respuesta es que, teniendo en cuenta alguna consideración extra, este tipo de expresiones se mantiene. Veamos qué pasa para el caso del índice 11. En la última expresión anterior teníamos 123456789 x 9 + 10. Ahora en el primer número habría que añadir el 10, pero añadiendo solo un dígito, lo cual es posible si lo hacemos como aparece en la siguiente imagen (se añade el 0 en la última posición y el 1 se suma a la posición anterior).

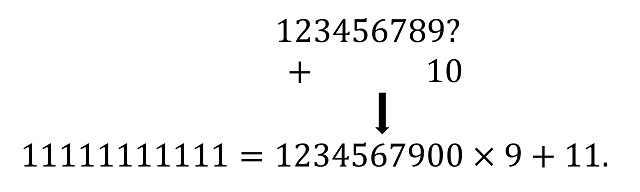
De esa misma forma se continua con 12, 13, 14, etc, algunos de ellos los mostramos en la siguiente imagen.

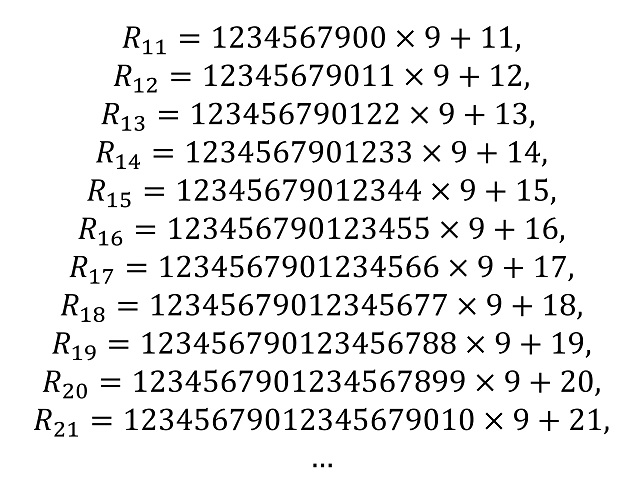
Vamos a terminar dividiendo los números repitunos por 9 y viendo qué ocurre.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.

2.- Albert H. Beiler, Recreations in the Theory of Numbers: The Queen of Mathematics Entertains, Dover, 1964.

3.- Página web: Numbers Aplenty.

4.- Página web: Enciclopedia On-line de Sucesiones de Números Enteros – OEIS

5.- Samuel Yates, The Mystique of Repunits, Mathematics Magazine, Vol. 51, No. 1, pp. 22-28, 1978.

6.- Gerard Villemin: nombres : curiosités – théorie – usage

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica