Mi libro La gran familia de los números (2021), de la colección Miradas matemáticas (Catarata, ICMAT, FESPM), está dedicado a algunas importantes familias de números naturales, entre los que están los números figurados, primos, capicúas, cíclicos, perfectos, amigos, intocables, narcisistas, felices o vampiros, entre muchos otros. Sin embargo, algunas curiosas familias de números quedaron fuera del mismo, ya que el espacio de un libro es limitado, como los llamados números parásitos, que van a ser presentados en esta entrada del Cuaderno de Cultura Científica, y de los que muchos aprendimos leyendo el libro El prodigio de los números, del divulgador científico estadounidense Clifford A. Pickover.

¿Cómo se definen los números parásitos?
Un número se dice que es un número parásito, o también número n-parásito, si al multiplicarlo por su último dígito -el de las unidades-, n, se obtiene un número con los mismos dígitos y en el mismo orden, salvo el último dígito que ha pasado a ser el primero. Por ejemplo, el número 102.564 es un número 4-parásito, puesto que si lo multiplicamos por 4 se obtiene el número 410.256.
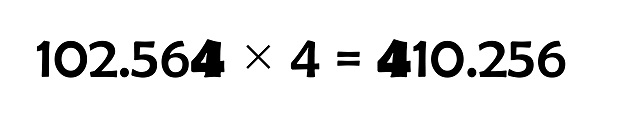
Pickover explica el nombre que ha dado a estos números de la siguiente forma:
“Este tipo de números recuerda la idea de un organismo biológico que contiene un parásito (dígito) que vaga por el cuerpo del organismo anfitrión (el número de varios dígitos en el cual reside el parásito), mientras gana energía alimentándose (la operación de multiplicación)”.
Si pensamos en un caso simple, cuando el número de las unidades, luego también el número por el que lo multiplicamos, es 1, se obtienen los números repitunos 1, 11, 111, 1.111, 11.1111, etcétera (de estos números hemos escrito en la entrada ¿Tienen algún interés los números repitunos, cuyos dígitos son todos unos?). Por este motivo, normalmente se habla de números n-parásitos, para n entre 2 y 9.
Mostremos un par de ejemplos más de números parásitos, el número 102.564.102.564 y el número 1.012.658.227.848 (que hemos tomado de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, en concreto, la sucesión A081463, formada por los números parásitos):

Cuando el número por el que multiplicamos, n, no coincide con el dígito de las unidades, Pickover habla de números seudoparásitos (o n-seudoparásitos), como el número 128.205, que multiplicado por 4 (que no es el dígito de las unidades, que es 5), da como resultado 512.820.
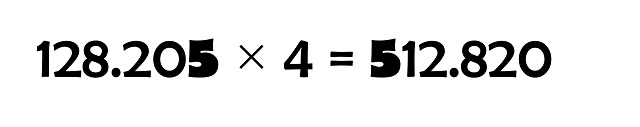
Algunos otros ejemplos de números seudoparásitos son:
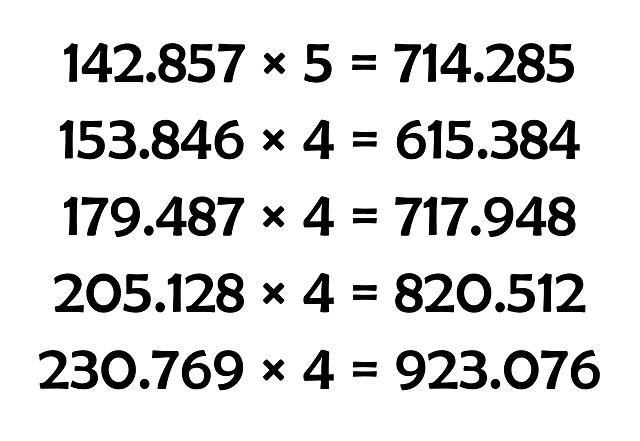
Existen una serie de números que están en la frontera de ser seudoparásitos, aquellos para los que podemos interpretar que tienen un cero a la izquierda, aunque en su representación claramente aparezca. Normalmente, no se considera que estos números, como el 25.641, sean números seudoparásitos, aunque se cumpla que al multiplicarlo por 4, el resultado sea 102.564, que como podemos interpretar que 25.641 es lo mismo que 025.641, se podría decir entonces que es un número 4-seudoparásito. Sin embargo, como comentábamos, lo usual es no considerar que pueda utilizarse el cero de esta manera.
En la literatura matemática actual, algunos autores utilizan el término “número parásito” para los dos tipos anteriores de números (parásitos y seudoparásitos), es decir, el número por el que multiplicamos no tiene que coincidir con el dígito de las unidades.
¿Cómo construir números parásitos?
Para ver cómo construir números parásitos, vamos a analizar primero cómo son estos números. Como sabemos, todo número N de m cifras, cuya representación decimal es N = am–1 am–2 … a2 a1 a0, tiene el valor
![]()
Ahora, si el número N es un número n-parásito o n-seudoparásito, entonces al multiplicarlo por el número de un solo dígito n (que en el caso de los parásitos es igual al dígito de las unidades a0), se obtiene el número A = a0am–1 am–2 … a2 a1, cuyo valor es
![]()
Luego, la condición de que N sea n-seudoparásito (parásito si n = a0) es que N multiplicado por n es igual a A. A partir de esta expresión y de los valores anteriores de N y A, se obtiene que la condición de que el número natural N sea n-seudoparásito es equivalente a que
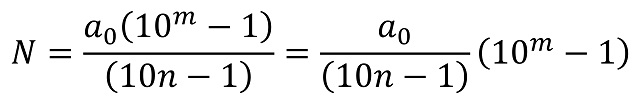
Luego ya tenemos la primera información útil, puesto que, si tenemos un número natural N expresado de esta forma, entonces es un número n-seudoparásito, con digito de las unidades a0.
Bueno, vamos a ver cómo construir números n-parásitos. Empecemos considerando el número racional n / (10 n – 1), que aparece en la expresión anterior, pero veámoslo en un caso particular, por ejemplo, n = 2. En tal caso, el número racional asociado a la construcción del número parásito es 2/19, que es el número decimal periódico, cuyo periodo es 105263157894736842, es decir,

que se repite de forma infinita. Ahora, recordemos que, si el periodo tiene m dígitos (en este ejemplo son 18), al multiplicar por 10m – 1 se obtiene el número natural que forma el periodo. En este caso, en particular, tenemos que
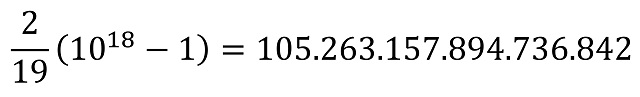
Por lo tanto, de lo anteriormente estudiado deducimos que 105.263.157.894.736.842 es un número 2-parásito.
Si volvemos al ejemplo inicial, que había propuesto Pickover, el número 4-parásito 102.564, veamos cómo lo habríamos generado. Como nuestro número de las unidades es n = 4, entonces consideramos el número racional n / (10 n – 1) = 4/39, que es un número decimal periódico, cuyo periodo es 102564, que tiene 6 dígitos. Es decir,
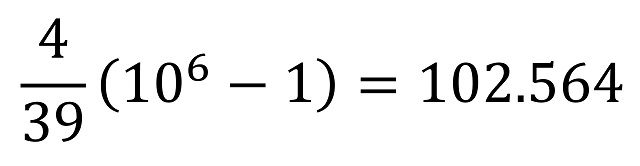
Y efectivamente, 102.564 es un número 4-parásito. Aprovechemos este ejemplo para comentar que del mismo se obtiene, lo que ocurre también para los demás ejemplos, que el número formado por k veces ese número n-parásito, sigue siendo n-parásito. Así, 102.564.102.564 o 102.564.102.564.102.564 también son números 4-parásitos, puesto que
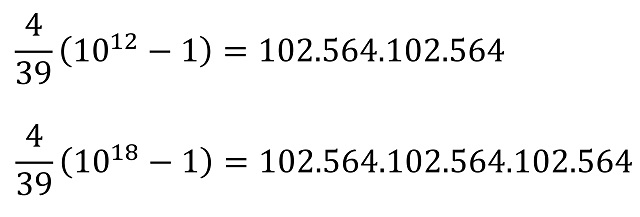
Con este método de construcción podemos obtener los números n-parásitos más pequeños para los diferentes valores de n, de 2 a 9, como se muestra en la siguiente tabla. Estos forman la sucesión A092697 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS.
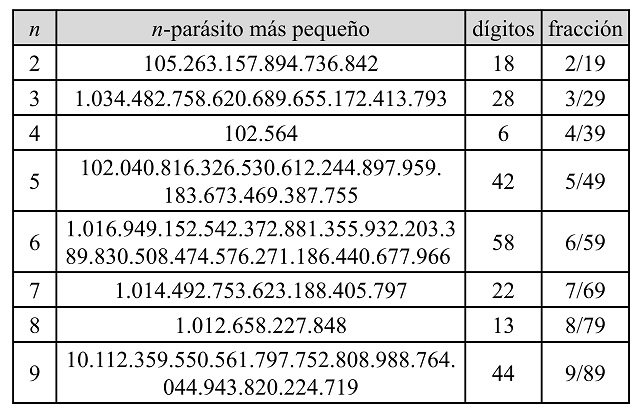
Claramente, la misma técnica sirve para crear números n-seudoparásitos. Tomemos el caso de la cifra multiplicativa n = 5, para los diferentes finales del número a0 (de 2 a 9). El resultado lo podemos ver en la siguiente imagen, en la que aparecen todos los números 5-seudoparásitos, con terminaciones entre 2 y 9 (más pequeños posibles para cada terminación). Los tres primeros pertenecen a ese grupo de números que se consideran, o no, seudoparásitos en función de si se permite jugar con el cero a la izquierda. Todos ellos tienen 42 dígitos (incluido el cero de la izquierda en los tres primeros casos), salvo uno de ellos, terminado en 7, que tiene 6 dígitos.

Algunas anécdotas parásitas
La primera anécdota, que aparece recogida en el libro El prodigio de los números, es una curiosidad relacionada con el número 5-parásito
102.040.816.326.530.612.244.897.959.183.673.469.387.755
que se puede escribir por parejas de dígitos, empezando en 1, que cada una es el doble de la siguiente (1) (02) (04) (08) (16) (32) y así se continúa. Aunque aquí tenemos que realizar cierta explicación. La siguiente pareja sería (64), sin embargo, en nuestro número parásito aparece (65), esto se debe a que la siguiente “pareja de dígitos” sería (128) que tiene tres dígitos, motivo por el cual el dígito 1 se suma a la anterior pareja, que pasa de (64) a (65). Y así se continúa con el resto, como aparece en la imagen.
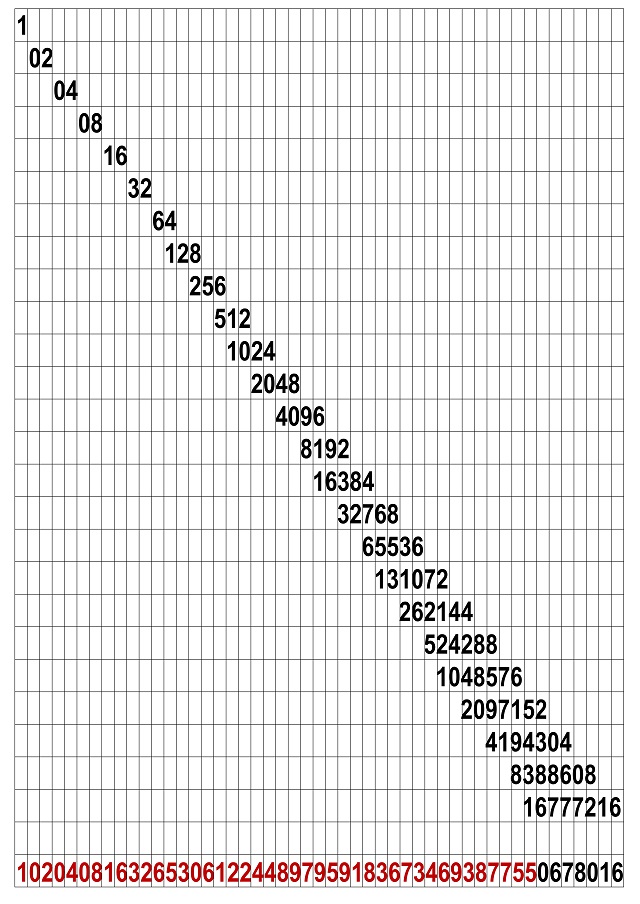
Y si continuásemos añadiendo filas (cada una con el número que dobla al anterior y colocado correctamente) se irían generando más copias del número seudoparásito, cada una a continuación de la siguiente (hacia la derecha).
La siguiente curiosidad la encontramos en el número 5-seudoparásito 142.857, que resulta ser un número cíclico (para más información sobre estos, véase el capítulo 3, titulado La simetría de los números, del libro La gran familia de los números). Entre otras propiedades este número satisface la propiedad de que multiplicado por los números 1, 2, 3, 4, 5 y 6, se obtiene un número con las mismas seis cifras, el mismo orden entre ellas, pero rotado cíclicamente, como se muestra en la siguiente imagen:

Además, si se multiplica por 7 el resultado es 999.999. Pero este no es el único número seudoparásito, o parásito, que es también cíclico. Otros son el 2-parásito 105.263.157.894.736.842, el 3-parásito 1.034.482.758.620.689.655.172.413.793, o el 6-parásito 1.016.949.152.542.372.881.355.932.203.389.830.508.474.576.271.186.440.677.966. Pero de los números cíclicos ya hablaremos en otra ocasión.

Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.
2.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
