En Coordenadas polares os hablé de mi afición por las fotografías con simetría circular. Pero no os conté toda la historia. No solo saco “fotos redondas”. Además, las “despolarizo”, por así decirlo. O, dicho de manera más precisa: utilizo un programa para mapear los píxeles de sus coordenadas polares, sobre los ejes cartesianos de una segunda imagen. Y además de eso, aplico una transformación exponencial sobre el radio, de manera que se conservan las proporciones de cada región en toda la imagen.

Pero… dicho así, creo que suena más complicado de lo que realmente es. Se entiende mucho más fácilmente con un par de imágenes. La idea es convertir la foto de la izquierda en la imagen de la derecha:

O, lo que es lo mismo (quizás con un esquema se entienda mejor):

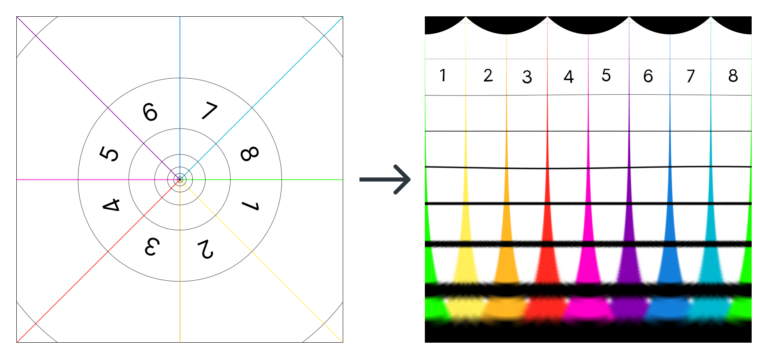
La transformación no se logra con un truco de Photoshop, ni con un filtro de ningún tipo. Es una aplicación de código abierto llamada depolarizer.

¿Qué es depolarizer?

Depolarizer es una aplicación de R creada por Iñaki Úcar y una servidora. El proyecto nació como un pequeño código de java que escribí para poder ejecutarlo desde FIJI. Pero Iñaki lo mejoró infinitamente y añadió una interfaz gráfica para que cualquier persona lo pueda instalar, y jugar con él fácilmente. Si queréis probarlo, solo tenéis que ir al repositorio de GitHub, descargar el código, y abrir la aplicación con RStudio. Una vez la ejecutéis, deberíais ver en vuestro navegador aparece una interfaz parecida a esta:

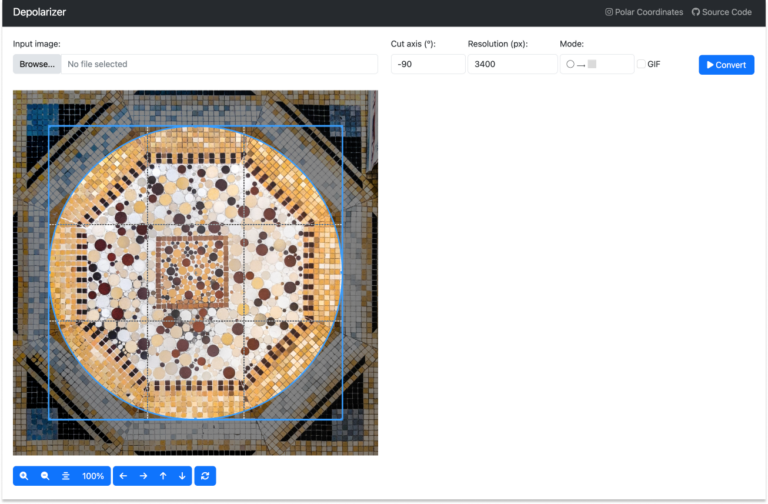
La interfaz está construida con ayuda de la librería shiny de R. Pero el alma de la aplicación vive en este archivito de Python, depolarizer.py. Es ahí donde se puede donde la imagen de entrada se transforma en su versión “despolarizada”. En concreto, en la función “to_polar”.

Voy a intentar a explicar cómo funciona. Pero no te preocupes: no hace falta saber programar para interpretar su código. Y si se te hace bola, siempre puedes saltar hasta la siguiente sección.

¿Cómo funciona el código?

La idea es más o menos como sigue:

1- Generamos una imagen de salida (pix₀), con la resolución la elegida (res₀).

Una imagen, en este contexto, no es más que una matriz, una estructura donde vamos a guardar los valores RGB de los pixeles de la nueva imagen. Las coordenadas de la imagen son los índices de cada elemento de la matriz.

En adelante utilizaremos los subíndices “i” de “input” y “o” de “output” para identificar las variables referidas a la imagen de entrada y de salida respectivamente.

2- Definimos algunas variables auxiliares de utilidad.

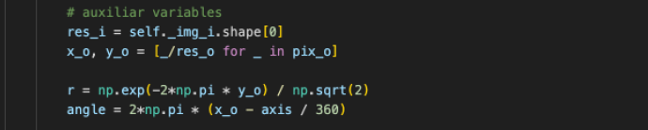
• La resolución de la imagen de entrada es res_i.
• Las variables x₀ e y₀ son las coordenadas de la imagen de salida normalizadas (dividimos sus valores entre la resolución de la imagen, para que vayan de 0 a 1).

Y aquí viene lo más interesante:

• Las coordenadas polares, r y Θ (angle), están definidas directamente sobre las coordenadas cartesianas de la imagen de salida, x₀ e y₀ . Es decir, cuando el programa “pinte” la imagen de salida (pix₀), en la dirección horizontal (x₀) veremos el ángulo (angle), y en la vertical (y₀), veremos el radio (r).
• En el caso de r, utilizamos una transformación exponencial. Y eso por qué, os preguntaréis, pues eso se merece su propio apartado, más abajo.

3- Definimos la función de mapeo, que es una transformación de coordenadas polares a cartesianas.

Lo que hará este mapeo es lo siguiente: el programa intentará rellenar los píxeles de la imagen de salida de uno en uno. Para saber “qué pintar” en cada pixel, buscará las coordenadas del pixel correspondiente en la imagen de entrada según diga el mapa.

¿Y qué es el mapa? ¡No es más que una función! La entrada de esa función son las coordenadas del pixel que queremos rellenar en la imagen final (x₀ , y₀) y la salida son las coordenadas correspondientes de la imagen inicial (x_i , y_i).

Si escribimos este código de manera más matemática, y obviamos la resolución (res_i = 1) quedaría algo así:

Pongamos, por ejemplo, que queremos rellenar el pixel situado en (x₀ , y₀) = (1/8, 0) . El programa utilizará estas coordenadas como input de las funciones map_x y map_y y encontrará las coordenadas del pixel correspondiente en la imagen de entrada. En este caso serían:

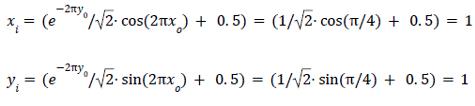
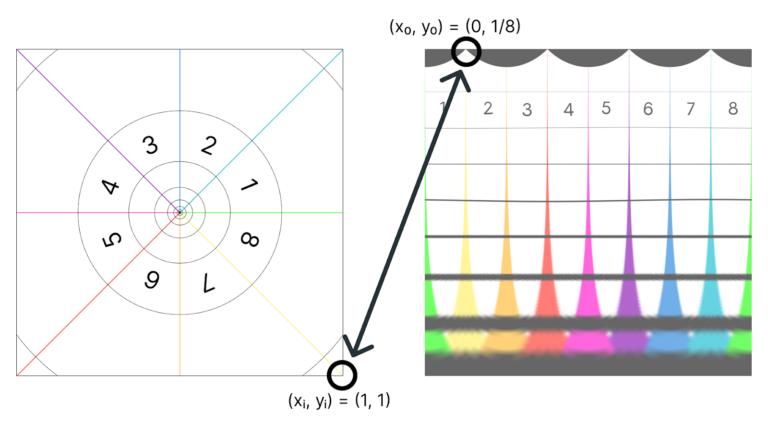
¿Y para qué sirve esa función exponencial?

La idea de “desenroscar” las imágenes mediante un cambio de coordenadas resulta más o menos intuitiva después de ver unos cuantos ejemplos. Pero puede que sea más difícil ver qué es lo que hace esa función exponencial sobre el radio. Quizás se entiende mejor si usamos el esquema anterior y representamos el cambio de coordenadas sin la función exponencial. El resultado sería este:

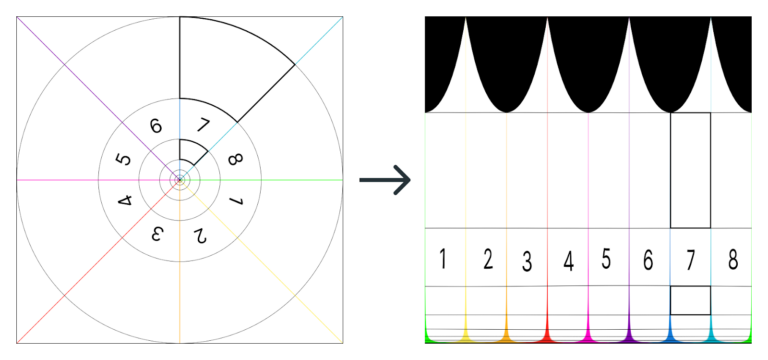
Fíjate en que todas las circunferencias de la imagen de entrada pasan a medir lo mismo en la de salida (son las líneas negras que van de izquierda a derecha). Pero, por eso mismo, el área entre las dos circunferencias más pequeñas queda mucho más “alargada” que la de la circunferencia mayor.

Mira lo que sucede, por ejemplo, con los dos “quesitos” subrayados en color negro. En la imagen de la izquierda los dos son muy parecidos: salvo por un factor de escala, tienen la misma forma. En la imagen de la derecha, en cambio, son muy distintos entre sí. La única manera de preservar las proporciones de todos los quesitos y evitar que distintos puntos de la superficie se deformen es utilizar una función exponencial, la misma que se oculta tras los sucesivos giros de la espiral maravillosa de Bernoulli.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica