Con esta entrada del Cuaderno de Cultura Científica cerramos una serie dedicada a tres curiosas superficies relacionadas con la banda de Moebius, a saber, el toro, la botella de Klein y el plano proyectivo real, y a cómo algunos artistas contemporáneos han representado estas superficies en sus obras de arte. La primera entrada, titulada El toro, la botella de Klein y el plano proyectivo real (I), estaba dedicada a la superficie del toro y se mostraban esculturas del artista japonés Keizo Ushio, del escultor minimalista estadounidense Richard Serra o del artista británico Jack Eagan, entre otros. Mientras que la segunda entrada, titulada El toro, la botella de Klein y el plano proyectivo real (II), se centraba en la superficie conocida con el nombre de botella de Klein y en obras de artistas como el mexicano Pedro Reyes, la parisina Bettina Samson o la matemática y artista argentina Moira Chas. Y la serie se cierra, en esta entrada, con el plano proyectivo real.

Todo empieza con una superficie rectangular

Antes de introducir la extraña superficie conocida con el nombre de plano proyectivo real, vamos a repasar cómo se construían el toro y la botella de Klein. Se empieza con una tira de papel rectangular ABCD (véase la siguiente imagen), en general, una superficie “topológica” rectangular, es decir, que nos permitiremos estirarla si fuese necesario, ya que estamos interesados en la creación de superficies topológicas, en este caso, el toro, la botella de Klein y el plano proyectivo real.

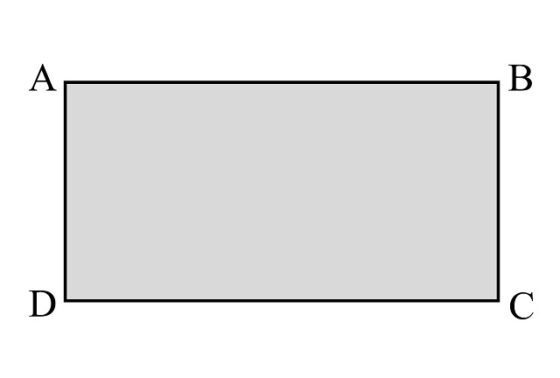
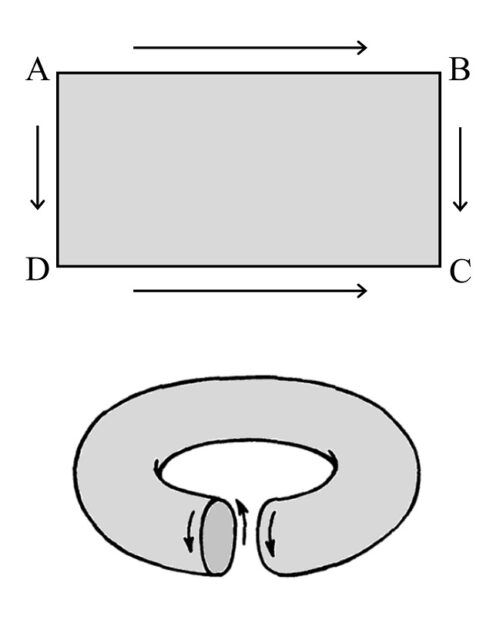
Dada esa superficie rectangular ABCD, si se pegan los lados AB con DC se obtiene un cilindro, pero en función de cómo se junten los otros dos lados se generan dos nuevas e interesantes superficies. Si lo hacen de forma directa (AD con BC, como indican las flechas de la siguiente imagen) será la superficie cerrada con dos caras, denominada en matemáticas “toro”, que tiene forma de rosquilla o flotador.

Si los otros dos lados se pegan en el sentido contrario (AD con CB), girando media vuelta antes de pegarse, entonces se construye la superficie topológica llamada “botella de Klein”, que es una superficie cerrada que solo tiene una cara. Como se explicaba en la anterior entrada y se muestra en la siguiente imagen, los extremos del cilindro no se pegan de forma directa, sino en sentido contrario, luego sería como si se pegaran “por detrás”. El problema es que para hacer esto tenemos que cruzar la propia superficie para poder unir esos dos extremos en la forma descrita. De esta manera, lo que se genera es una “representación” de la botella de Klein que se autointerseca, como se muestra en la imagen.

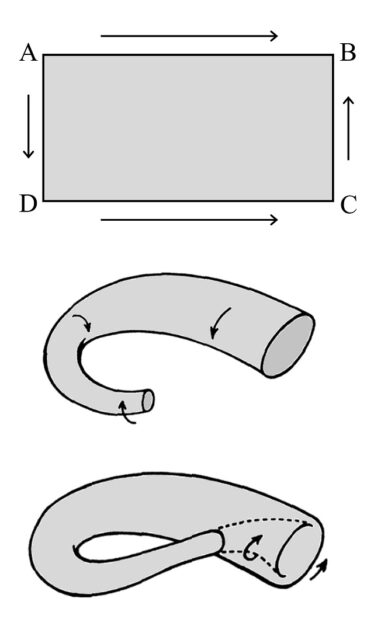
También explicábamos en la anterior entrada, que la botella de Klein, tal cual la hemos definido, no debiera de tener autointersecciones. El problema está en que esta construcción geométrica “ideal” no genera una superficie que esté dentro de nuestro espacio tridimensional, sino que su espacio natural es el espacio de dimensión cuatro, y aquí nos encontramos con un gran problema, ya que no somos capaces de visualizar la cuarta dimensión. Por este motivo, nos quedábamos en la anterior entrada con esta representación, que al menos habita en el espacio visual, el espacio de dimensión tres.

Un material muy interesante para observar y entender bien la botella de Klein, en particular, su realización en el espacio tridimensional, es el cristal. En la siguiente imagen podéis disfrutar de una botella de Klein realizada en cristal. Aquí os presento mi botella de Klein construida en cristal, que me ha regalado la junta directiva de la Sociedad Madrileña de Profesores de Matemáticas (SMPM) Emma Castelnuovo, por mi participación en las jornadas formativas de enseñanza y aprendizaje de las matemáticas, de este año 2023. ¡Muchísimas gracias por tan hermoso presente!

Por otra parte, mi amiga Mariel García, la conocida “Mariel Mates”, que tiene hermosas creaciones textiles relacionadas con las matemáticas, como las geniales y coloridas bufandas “pi-bufanda” y “fibo-bufanda”, ha tejido recientemente una interesante y hermosa botella de Klein, que podéis ver en la siguiente imagen.

El plano proyectivo real

La superficie que nos ocupa para cerrar esta serie, el plano proyectivo real, es una interesante superficie desde el punto de vista matemático, pero también complicada de entender, aunque vamos a intentar definirla siguiendo la línea constructiva que hemos trazado en esta serie.

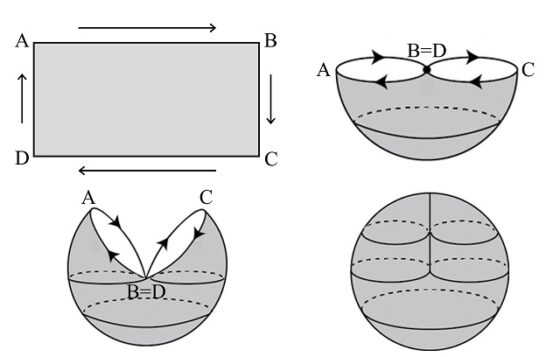
Volviendo a nuestra tira rectangular ABCD, si se pegan los dos extremos opuestos, pero girando media vuelta uno de los extremos, por ejemplo, en el rectángulo de la siguiente imagen se pega AD con CB, se forma la banda de Moebius, como ya hemos explicado en muchas entradas anteriores y mostramos en la siguiente imagen.

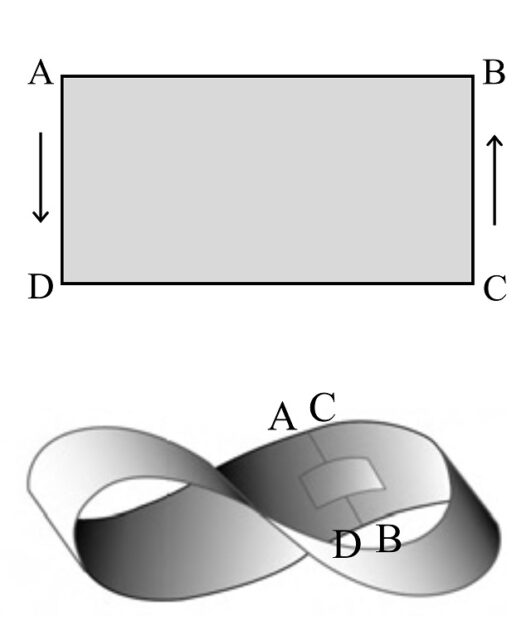
Pero, si ahora, dada esa banda de Moebius, pegamos los otros dos extremos del rectángulo, girando media vuelta de nuevo a uno de ellos, es decir, se pega AB con CD, se obtiene la conocida superficie denominada “el plano proyectivo real”, que resulta ser otra superficie cerrada (sin borde) con una sola cara. Para intentar realizar una “imagen” de esta superficie, tenemos que darnos cuenta de que las dos parejas de lados opuestos del rectángulo ABCD se pegan en sentido contrario, DA con BC y AB con CD. Esta forma de pegar los lados opuestos es como si pegáramos DAB con BCD, como se muestra en la siguiente imagen. El problema está, de nuevo, que no hay forma de pegar DAB con BCD sin pasar a través de la propia superficie, por lo que la imagen que se muestra a continuación es una realización tridimensional, con autointersecciones, del plano proyectivo real (que se conoce con el nombre de “gorra cruzada”, del inglés “cross cap”). Al igual que ocurría con la botella de Klein, el plano proyectivo real tampoco está, de forma natural, en el espacio tridimensional, sino que habita de forma natural en el espacio de dimensión cuatro. Por lo tanto, lo que nosotros podemos ver son proyecciones del plano proyectivo real, que existe en el espacio de dimensión cuatro, sobre el espacio tridimensional. Luego no vemos toda su realidad, sino proyecciones del mismo.

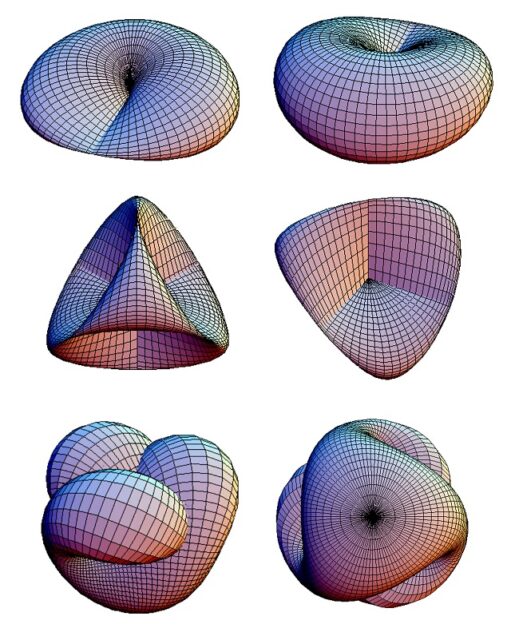
Como acabamos de comentar, el plano proyectivo real es una superficie que, por su construcción, no se puede representar en el espacio tridimensional (nuestro espacio visual y mental), sino que vive en el espacio de dimensión cuatro. Por este motivo, al proyectarlo en el espacio tridimensional se producen auto-intersecciones, como en la representación anterior. Aunque no vamos a explicar su origen, existen otras formas de representar/proyectar el plano proyectivo real en el espacio tridimensional. Tres representaciones clásicas del plano proyectivo real son el sombrero cruzado, que ya hemos mostrado, la superficie de Boy (que recibe su nombre del matemático alemán Werner Boy (1879-1914), quien descubrió esta superficie en 1901, cuando su director de tesis, el matemático alemán David Hilbert (1862-1943) le pidió que demostrase que era imposible realizar una “inmersión” del plano proyectivo real en el espacio tridimensional) y la superficie romana de Steiner (que recibe su nombre del matemático suizo Jakob Steiner (1896-1963), quien la descubrió en 1844, en un viaje a Roma), que se muestran, con dos puntos de vista distintos de cada una de ellas, en la siguiente imagen.

Esculpiendo el plano proyectivo real

Nos encontramos ante una superficie geométrica compleja y crear una escultura con alguna de sus realizaciones tridimensionales no es una tarea sencilla, por lo que algunos de los trabajos artísticos sobre las mismas los desarrollan artistas con formación matemática o que colaboran con personas del ámbito de las matemáticas.

El primer artista que traemos a esta entrada es el escultor y matemático estadounidense Helaman Ferguson (1940), de quien ya explicamos su obra Toro umbilical (1988) en la entrada Arte Moebius (II). Ferguson es uno de esos artistas cuyo arte podríamos denominar “arte matemático”, ya que sus esculturas tienen una fuerte componente matemática. En particular, trabaja mucho con superficies topológicas, como las que nos ocupan en esta serie. Sobre la relación entre escultura y matemáticas Helaman Ferguson dice lo siguiente: “creo que la escultura es una forma muy poderosa de transmitir las matemáticas, y estas son un lenguaje de creación muy poderoso para la escultura”.

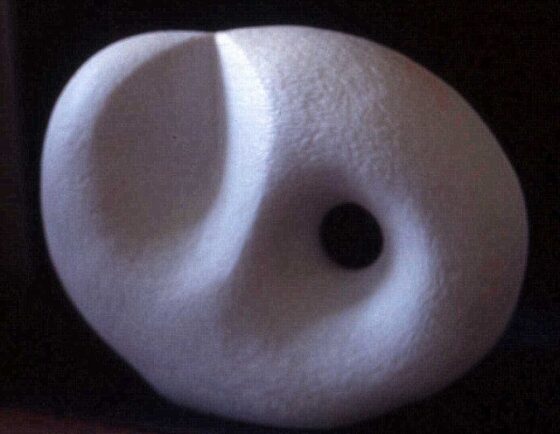
La escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1989), realizada en bronce, no es una escultura de la realización tridimensional del plano proyectivo real denominada gorra cruzada, que acabamos de explicar más arriba, sino de una nueva superficie que está formada por la unión de la gorra cruzada con la superficie del toro.

Además, realizó una segunda versión en mármol blanco, que mostramos en la siguiente imagen.

Nuestra siguiente artista también se ha formado en matemáticas, de hecho, tiene formación tanto en matemáticas, como en bellas artes. Se trata de la matemática y artista estadounidense Camila Friedman-Gerlicz. Ella ha realizado una curiosa instalación de la superficie de la gorra cruzada, titulada Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), que consiste en una escultura de madera muy especial, con la forma de la gorra cruzada, un dispositivo rectangular táctil en la base de la escultura, como se muestra en la siguiente imagen, y un sistema de luces dentro de la gorra cruzada de madera.

¿Cómo funciona la instalación? Es lo que en matemáticas llamamos una parametrización de la superficie de la gorra cruzada, es decir, cada punto del rectángulo de la base se corresponde con un punto de la superficie. De hecho, en esta instalación cuando se coloca un dedo en un punto del rectángulo táctil de la base se ilumina el correspondiente punto de la superficie, y si vamos moviendo nuestro dedo por el rectángulo se va moviendo la luz por la superficie de madera, visualizando así la relación entre el rectángulo generador y la realización, denominada gorra cruzada, del plano proyectivo real.

Esta artista, cuyo arte está muy conectado con las matemáticas, también ha realizado una superficie de la gorra cruzada en cerámica, que es uno de los materiales con los que más trabaja. También en cerámica ha realizado otra de las realizaciones tridimensionales del plano proyectivo real, la superficie de Boy, que hemos mostrado más arriba.

Además, ha creado una escultura colgante en papel, que consiste en una triangulación de la superficie de Boy, es decir, ha representado una superficie poliédrica creada por triángulos, los cuales forman la superficie topológica descubierta por Werner Boy.

Esta artista matemática también tiene hermosas botellas de Klein realizadas en cerámica, que podéis encontrar en su cuenta de instagram.

Continuando con la superficie de Boy, una de las esculturas más conocidas de la misma dentro de la comunidad matemática, es la escultura que se encuentra en el exterior del Instituto de Investigación Matemática Oberwolfach, ubicado en la Selva Negra alemana (sobre el mismo escribí en la entrada Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática). Esta escultura fue un regalo al instituto IMO de la empresa alemana Mercedes-Benz, que fue realizada en 1991 a partir de las computaciones realizadas por los matemáticos Hermann Karcher, Ulrich Pinkall e Ivan Sterling del Max Planck Institut für Mathematik en Bonn (Alemania).

El desarrollo de las impresoras 3D está permitiendo realizar hermosas esculturas de superficies matemáticas complejas de forma bastante sencilla. En particular, algunos artistas y artesanos están trabajando en esta línea y podemos encontrar, y comprar, curiosos y hermosos diseños en internet. Por ejemplo, el arquitecto, diseñador y matemático Rick Russell entre sus “Mathematical Creations” podemos encontrar esta Boy’ Surface Mesh / Malla de la superficie de Boy, cuyo tamaño es 6.25 x 6.38 x 4.72 cm, y está impresa en plástico metálico y acero bañado en oro.

O esta otra pieza que representa también la superficie de Boy, pero con color y agujeros, realizada por el artista y fabricante Benjamin Berger, que es la persona que está detrás de Implicit Art.

Si seguimos con objetos realizados con impresión 3D, también nos encontramos a la superficie romana de Steiner. Por ejemplo, el diseñador y fabricante Paul Summers, que es quien está detrás de los diseños de FluidDesigner, ha realizado el diseño de unos pendientes con forma de corazón, que realmente es la superficie de Steiner, que podéis admirar en la siguiente imagen.

Vamos a concluir esta entrada del Cuaderno de Cultura Científica con una escultura de la artista minimalista alemana-estadounidense Ruth Vollmer (1903-1982), relacionada con la escuela de la Bauhaus, con el título de Superficie de Steiner (1979), realizada en metacrilato, de la que también realizaría una versión con colores.

Bibliografía

1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, colección Miradas matemáticas, Catarata, 2023.

2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.

3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.

4.- Stephen Barr, Experiments in Topology, Dover, 1989.

5.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.

6.- Raúl Ibáñez, La cuarta dimensión, RBA, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica