Cuando escribes un libro una de las tareas necesarias en su desarrollo es la elección del material que tiene que estar incluido necesariamente en el libro y el que debes dejar fuera, aunque te parezca muy interesante. En mi último libro, titulado Las matemáticas como herramienta de creación artística, también me ha tocado dejar fuera muchos materiales muy interesantes. Por ejemplo, en el capítulo titulado Topología: la banda de Moebius, mi idea original era haber incluido obras de arte relacionadas tanto con la banda de Moebius, que son muchas (algunos ejemplos los hemos comentado en las entradas del Cuaderno de Cultura Científica Arte Moebius (I) y Arte Moebius (II), así como en el mencionado libro), como con otras tres superficies relacionadas, que son el toro, la botella de Klein y el plano proyectivo real.

Esta serie de entradas del Cuaderno de Cultura Científica vamos a hablar de estas tres superficies, el toro, la botella de Klein y el plano proyectivo real, y de cómo algunos artistas las han representado en sus obras.
La banda de Moebius
Empecemos recordando qué es una banda de Moebius, que es uno de los objetos más curiosos de la topología puesto que es una superficie con una sola cara y un solo borde.
Dada una tira de papel rectangular ABCD (véase la siguiente imagen), si se pegan los extremos (AB con DC) se obtendrá una banda normal, que es una superficie con dos caras –interior y exterior- y dos bordes –arriba y abajo-. Vamos, lo que podemos considerar normal en una superficie, que tenga dos caras (aunque rompiendo esa intuición, ya en la entrada La hoja de papel con cuatro caras, una propuesta de taller mostrábamos cómo construir una mágica “hoja de papel” con cuatro caras).
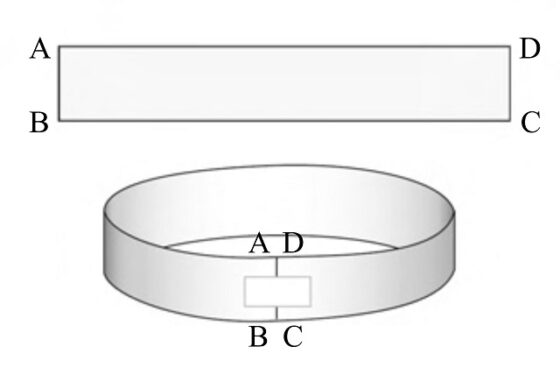
Sin embargo, si primero giramos uno de los extremos del papel media vuelta y después los juntamos (ahora AB se “pega” con CD) se obtiene una banda retorcida, que tiene una sola cara (si se intenta pintar de forma continua la nueva superficie solamente se podrá utilizar un color, mientras que a la anterior se le pueden aplicar dos colores distintos, uno para el interior y otro para el exterior) y un solo borde (que también se puede perfilar de forma continua). Esta es la conocida como superficie de Moebius, que fue descubierta (dentro de las matemáticas), de forma independiente, por los matemáticos alemanes Johann Benedict Listing (1808-1882) y August Ferdinand Moebius (1790-1868).
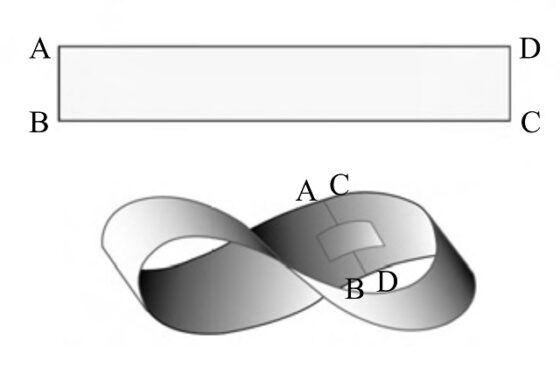
¿Qué ocurre si en lugar de girar uno de los extremos del papel media vuelta se gira una vuelta entera y después se juntan ambos extremos (de nuevo, AB con DC)? Lo que ocurre es que ahora se obtiene una banda retorcida que tiene, de nuevo, dos caras y dos bordes, como podéis comprobar fácilmente simplemente utilizando una tira rectangular alargada de papel.
La banda de Moebius es una superficie con curiosas propiedades y aplicaciones, algunas de ellas se pueden leer en las entradas del Cuaderno de Cultura Científica ya mencionadas o en otras entradas como En busca de la banda de Moebius más corta posible o Dibujando grafos sobre la banda de Moebius, o también en los libros La banda de Moebius, de Clifford Pickover, Experiments in Topology, de Stephen Barr o Festival mágico-matemático, de Martin Gardner. En particular, existen muchos experimentos que consisten en cortar tiras de papel, como los clásicos en los que se corta la banda de Moebius de papel longitudinalmente por la mitad o por un tercio de la anchura, con resultados asombrosos, o algunos algo menos conocidos como el de cómo construir dos corazones entrelazados o un cuadrado, partiendo de dos cintas de Moebius pegadas, o cómo construir un slip de Moebius, que pueden verse como actividades del libro Las matemáticas como herramienta de creación artística.

Para finalizar este apartado, mencionaremos que, aunque la superficie de Moebius fue descubierta dentro de las matemáticas en el siglo xix, esta ya era conocida con anterioridad. La banda de una sola cara se encuentra, por ejemplo, en motivos decorativos antiguos, como algunos mosaicos romanos (alrededor del año 200), como se menciona en el artículo The Möbius band in Roman mosaics (Scientific American 61, 1973) de L. L. Larison, o en el artículo Möbius strips before Möbius: Topological hints in ancient representations (The Mathematical Intelligencer 38, 2016), de J. H. E. Cartwright y D. L. González.

La superficie del toro
A partir de la definición de las bandas normal (que topológicamente es un cilindro) y de Moebius se pueden definir nuevas superficies que también tendrán una o dos caras, pero que no tendrán bordes. Si volvemos a un rectángulo ABCD, sabemos que pegando los lados AB con DC se obtiene un cilindro, pero en función de cómo se junten los otros dos lados generaremos dos nuevas e interesantes superficies. Si lo hacen de forma directa (AD con BC, como indican las flechas de la siguiente imagen) se obtiene una superficie cerrada -es decir, que no tiene bordes- con dos caras, que tiene forma de rosquilla o flotador, conocida en matemáticas como toro (que no tiene nada que ver con el animal, sino que el término toro, para designar la superficie, viene de la palabra latina “torus”, que tiene un significado de “bulto, protuberancia o nudo”).
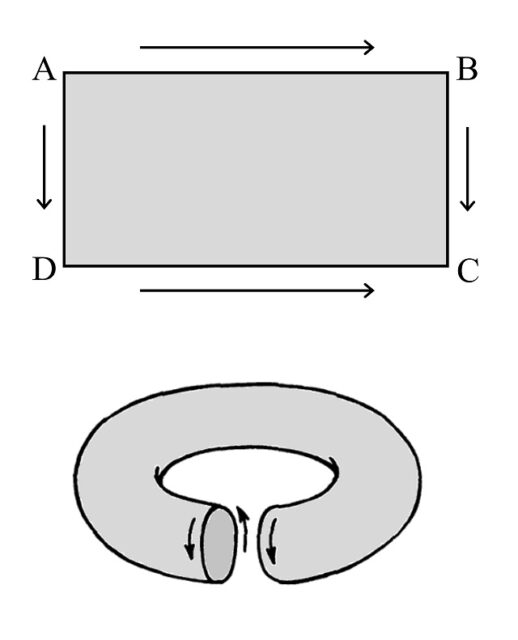
El toro, tanto geométrico, es decir, la superficie del flotador, que es la superficie de revolución de un círculo alrededor de una recta exterior, como topológico (véase la entrada La topología modifica la trayectoria de los peces para leer más sobre el concepto de topología), esto es, deformaciones “topológicas” (manteniendo cierta continuidad) del toro geométrico, también ha sido utilizado en el arte contemporáneo. A continuación, mostraremos algunos ejemplos.
El toro en la obra artística de Keizo Ushio
En la entrada Arte Moebius (II), ya mostrábamos un hermoso ejemplo de escultura que es un toro con una banda de Moebius dentro, es la escultura Moebius en el espacio (2005), del escultor japonés Keizo Ushio (Fukusaki, Prefectura de Hyogo, 1951), un artista con una obra escultórica muy geométrica. En Moebius en el espacio (véase la imagen más adelante), como en algunas otras obras similares, se representa el “espacio exterior” de la superficie de Moebius, mientras que esta no es más que el “espacio vacío”. El problema plástico de esta idea es hacer visible ese espacio vacío en la escultura. Para ello, Ushio trabaja con el toro sólido (realizado en granito), que va a jugar el papel de “espacio exterior” y después perfora una serie de diámetros que van girando, desde un primer diámetro vertical, de manera que al llegar al punto de partida han dado media vuelta, 180 grados, que de nuevo es el diámetro vertical. Ese espacio vacío dentro del toro tiene, por tanto, la forma de la banda de Moebius.


Esta construcción artística le ha llevado al artista japonés Keizo Ushio a crear hermosas esculturas como la mencionada Moebius en el espacio (2005). En la misma, para destacar aún más la banda de Moebius ausente, ha pintado de naranja la zona del toro que estaría en contacto directo con ella, como se ve en la siguiente fotografía. Una impactante escultura.

Como la banda de Moebius tiene una sola cara, el espacio exterior a la misma, que es el toro sólido de granito en la escultura, es único también, luego al perforar la banda de Moebius en el toro, este sigue siendo de una sola pieza, que se corresponde con esa única cara de la “banda de Moebius vacía”. Esto no ocurre si se perforara en el toro una banda con dos caras, como vamos a mostrar a continuación.
Conocí al escultor Keizo Ushio en el International Congress of Mathematicians que organizamos en Madrid en agosto de 2006, cuando le invitamos a realizar una escultura en vivo en el exterior del Palacio Municipal de Congresos de Madrid. Fue una experiencia increíble, que disfrutaron todas las personas que pasaron por allí esos días. La escultura que realizó entonces fue Oushi-Zokei ICM Madrid 2006 (véase la siguiente imagen), que en la actualidad se encuentra en el exterior del ICMAT (Instituto de Ciencias Matemáticas, del CSIC), de Madrid. En esta escultura, en lugar de perforar los diámetros del toro girando media vuelta, lo hizo girando una vuelta entera, por lo tanto, obteniendo una banda normal retorcida en su interior (con dos caras como se ha explicado más arriba). Como el espacio vacío dentro del toro sólido (granito) es una banda con dos caras, entonces la escultura se separa en dos partes, cada una se corresponde con una cara.

El toro en la obra artística de Richard Serra
El toro es una superficie con interesantes propiedades que se estudian tanto en geometría, como en topología. Yo enseño esta superficie en la asignatura “Curvas y superficies” del grado de matemáticas, en particular, cuando explico la curvatura de una superficie. El tema de la curvatura de una superficie no es un tema sencillo para tratar en esta entrada, puesto que hay diferentes tipos de curvatura asociados al estudio de las superficies –curvaturas normales, curvaturas principales, curvatura de Gauss y curvatura media- y es necesario conocer algunas herramientas de geometría diferencial para entenderlo, aunque para hablar de las esculturas de Richard Serra nos bastará con explicar el significado del signo de la conocida como curvatura de Gauss (que es una curvatura intrínseca de la superficie).
La curvatura de Gauss es un concepto local, es decir, cambia de unos puntos a otros de la superficie, pero para explicar el significado del signo de esta curvatura vamos a considerar superficies con curvatura constante, es decir, con la misma curvatura en todos sus puntos: el plano o el cilindro (este lo podemos ver como un trozo rectangular de plano en el que pegamos dos lados opuestos), que tiene curvatura cero, la esfera, que tiene curvatura positiva, y el hiperboloide de una hoja, que tiene curvatura negativa, cuyo significado explicaremos a continuación. Primero una imagen de estas tres superficies.
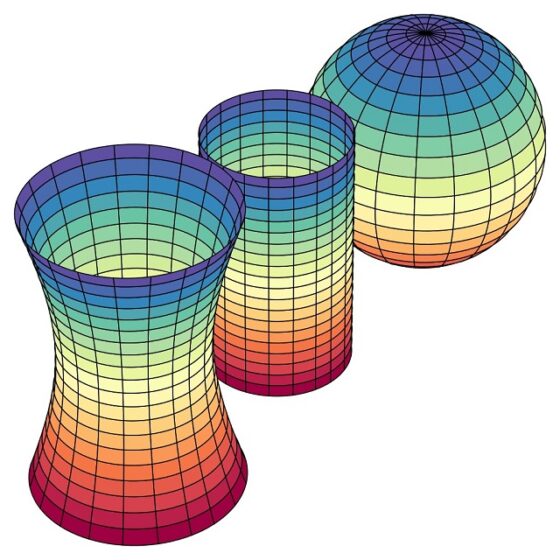
El plano tiene curvatura de Gauss cero, ya que no se curva de ninguna de las formas, y también el cilindro (esta superficie nos puede despistar ya que aparentemente sí tiene curvatura, pero la curvatura que tiene es la curvatura extrínseca –la llamada curvatura media-, que es no nula, pero la intrínseca, la curvatura de Gauss es cero, ya que el cilindro es como un trozo rectangular de plano en el que pegamos dos lados opuestos).
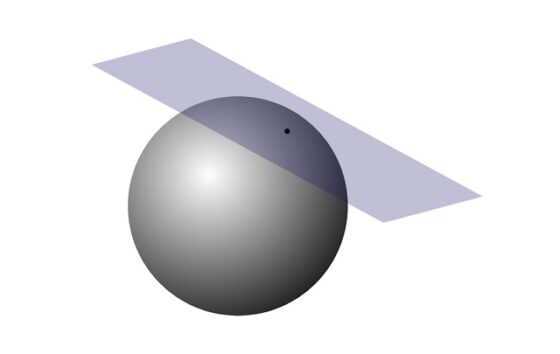
La esfera tiene curvatura de Gauss positiva, lo cual implica que, si tomamos el plano tangente a la esfera en cualquier punto, la esfera queda entera a un lado del plano tangente, como se muestra en la siguiente imagen. Otra forma de verlo –que nos ayudará a entender las esculturas de Richard Serra- es que, si tenemos una esfera gigante y colocamos nuestra cara en un punto de la misma, por ejemplo, en el exterior de la superficie, entonces la esfera se aleja de nosotros en todas las direcciones, es decir, la esfera es convexa en todas las direcciones (si nuestra cara está en el interior de la esfera entonces la esfera nos envuelve en todas las direcciones, esto es, la esfera es cóncava en todas las direcciones).
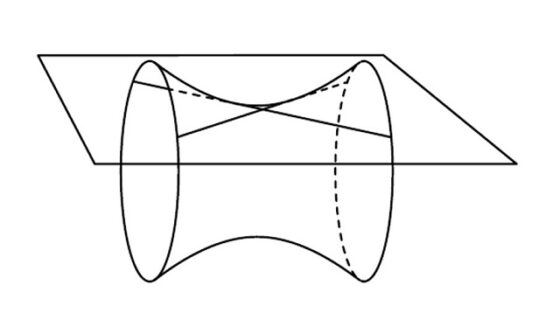
El hiperboloide de una hoja tiene curvatura de Gauss negativa, lo cual implica que, si tomamos el plano tangente al hiperboloide en cualquier punto, este corta al hiperboloide y la superficie tendrá partes a ambos lados del plano tangente, como se muestra en la siguiente imagen. Al igual que para la esfera, otra forma de verlo es que, si tenemos un hiperboloide gigante y colocamos nuestra cara en un punto del mismo, entonces el hiperboloide se aleja en algunas direcciones (será convexo en ellas), mientras que en otras direcciones nos envuelve (es cóncava en las mismas).
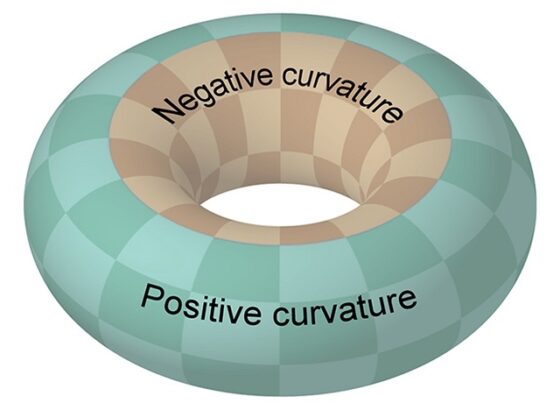
¿Qué ocurre para el toro (geométrico)? Esta superficie tiene puntos con curvatura de Gauss positiva (los del exterior) y puntos con curvatura de Gauss negativa (los del interior), con puntos de curvatura nula en las circunferencias que separan el interior y el exterior, como se muestra en la imagen.
Ya estamos en condiciones de entender la importancia de la curvatura de Gauss en algunas de las esculturas del escultor minimalista estadounidense Richard Serra (San Francisco, California, 1938), como New Union / Nueva unión (2003), que durante muchos años pudimos disfrutar en el exterior del Museo de Bellas Artes de Bilbao, o Between the Torus and the Sphere / Entre el toro y la esfera (2003-2005) y Blind Spot Reversed / Punto ciego invertido (2003-2005), que podemos ver en el Museo Guggenheim de Bilbao.

Richard Serra contrapone, en estas esculturas, dos trozos de superficies con distinto signo de la curvatura de Gauss, positivo (esfera) y negativo (interior del toro). Las tres esculturas están formadas por planchas alargadas que son trozos de esfera (curvatura positiva) y planchas alargadas que son trozos de la parte interior del toro (curvatura negativa). Y lo interesantes de ellas es que la curvatura no solo se puede percibir visualmente desde lejos, sino que cuando caminamos entre las planchas de esculturas como Entre el toro y la esfera podemos percibir la curvatura interaccionando con nosotros. Yo suelo recomendar a mis estudiantes, o a las personas a las que les explico esta obra, que se coloquen frente a una plancha esférica, con la nariz tocando la plancha y se den cuenta de que el acero de la misma se aleja (o nos envuelve si estamos en la parte interior de la esfera) en todas las direcciones, lo que ocurre por ser de curvatura positiva. Y que después pasen a una plancha tórica, de nuevo con la nariz tocando el acero y se den cuenta de que en unas direcciones la superficie se aleja de nosotros y en otras nos envuelve, debido a que esa zona del toro tiene curvatura negativa.
El toro anudado
Realmente hay muchos artistas que han realizado esculturas con la forma de un toro geométrico. Pongamos un par de ejemplos más. Uno es el artista británico Jack Eagan y su serie de esculturas Eroded torus / Toro erosionado, dos de las cuales, realizadas en bronce, se muestran en las siguientes imágenes.


Y el otro ejemplo es el artista británico John Robinson (1935-2007) y su escultura Bonds of Friendship / Lazos de amistad (1980), en la que se representan dos toros entrelazados.

Pero me gustaría terminar esta entrada del Cuaderno de Cultura Científica con una serie de esculturas más topológicas que tienen al toro como su principal protagonista, y que nos relacionan al toro topológico con la teoría de nudos, que es otra parte muy interesante de la topología (para leer sobre la teoría de nudos os recomiendo las entradas La topología modifica la trayectoria de los peces, La artista Anni Albers, The Walking Dead y la teoría de nudos y Del nudo gordiano al nudo de los enamorados, por territorio matemático).
En matemáticas, un nudo es una curva cerrada en el espacio y la teoría de nudos estudia cuántos nudos distintos, es decir, topológicamente diferentes, existen, así como propiedades topológicas de los mismos. Algunos escultores realizan esculturas de toros anudados, es decir, tienen la forma de nudos, por ejemplo, como el nudo de trébol, pero desde el punto de vista de la topología “son” un toro. Es como si partiéramos de un cilindro, realizáramos un nudo y luego pegáramos los extremos, transformándolo en un toro anudado.
Mostremos dos ejemplos de esculturas de toros anudados. La primera es de la escultora estadounidense E. Calder Powel, que primero estudió matemáticas, que se nota en su trabajo artístico, y después estudió arte. La escultura Nudo de trébol, que se muestra en la siguiente imagen, es un toro anudado con la forma del nudo de trébol.

Y terminamos con una escultura que tuve la suerte de ver este verano, cuando fui a visitar la torre del arquitecto Frank Gehry que alberga el centro cultural Luma, en Arlés (Francia). Se trata de un nudo tórico rosa muy llamativo, la escultura Krauses Gekröse (2011), del escultor austriaco Franz West (1947-2012), que vemos en la siguiente imagen. El nudo implicado en esta obra es la unión (en topología “suma conexa”) de dos nudos de trébol, lo que se conoce como nudo de rizo.

Bibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, colección Miradas matemáticas, Catarata, 2023.
2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.
3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.
4.- Stephen Barr, Experiments in Topology, Dover, 1989.
5.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.
6.- Página web del escultor Keizo Ushio
7.- Richard Serra, La materia del tiempo / Denboraren materia, Museo Guggenheim Bilbao, 2006.
8.- Página web de Jack Eagan
9.- Bradshaw Foundation: Symbolic Sculpture. The collected Works of John Robinson
10. Página de la escultora E. Calder Powel
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Una banda de Moebius de chocolate — Cuaderno de Cultura Científica
[…] mi última entrada del Cuaderno de Cultura Científica, titulada El toro, la botella de Klein y el plano proyectivo real (I), he iniciado una serie dedicada a la superficie del toro, la botella de Klein y el plano proyectivo […]
El toro, la botella de Klein y el plano proyectivo real (II) — Cuaderno de Cultura Científica
[…] la entrada del Cuaderno de Cultura Científica El toro, la botella de Klein y el plano proyectivo real (I) iniciamos una serie sobre tres superficies relacionadas con la banda de Moebius, a saber, el toro, […]
El toro, la botella de Klein y el plano proyectivo real (III) — Cuaderno de Cultura Científica
[…] han representado estas superficies en sus obras de arte. La primera entrada, titulada El toro, la botella de Klein y el plano proyectivo real (I), estaba dedicada a la superficie del toro y se mostraban esculturas del artista japonés Keizo […]