Hace unos cuantos días, pensando en la situación de confinamiento en la que nos encontramos en estos momentos, me pareció que sería una buena idea preparar una actividad sencilla para enviar a la gente y que pudieran realizarla en su casa. Mi idea era que fuese una actividad para personas de cualquier edad, desde pequeños (acompañados si es necesario) hasta mayores. Entonces, me decidí por un taller que hago desde hace algunos años, aunque relacionado con otras cuestiones, y que me gusta mucho. Consiste en construir un objeto matemático sencillo y sorprendente, una hoja de papel con cuatro caras.
Este objeto matemático, cuyas instrucciones de construcción os voy a explicar en esta entrada del Cuaderno de Cultura Científica, pertenece a la familia de objetos llamados flexágonos y que fue descubierta por el matemático inglés Arthur Stone, de quien ya hemos hablado en relación con el problema de la cuadratura del cuadrado en 1939. Aunque estos objetos fueron dados a conocer y popularizados por el gran divulgador de las matemáticas Martin Gardner (1914-2010) en su columna Juegos matemáticos de la revista Scientific American. En concreto, el objeto matemático que vamos a construir en esta entrada es un tetraflexágono, es decir, un flexágono con cuatro lados (cuadrado o rectángulo), además, como va a poder mostrar cuatro caras, se denomina un tetratetraflexágono.

Pero vayamos directamente a nuestro objeto matemático, esa hoja de papel de cuatro caras, el tetratetraflexágono, y a su construcción: materiales e instrucciones.
Material básico para el taller: una hoja de papel normal, por ejemplo, din A4, un lápiz y una regla.
Instrucciones para construir el tetratetraflexágono, la hoja de papel con cuatro caras:
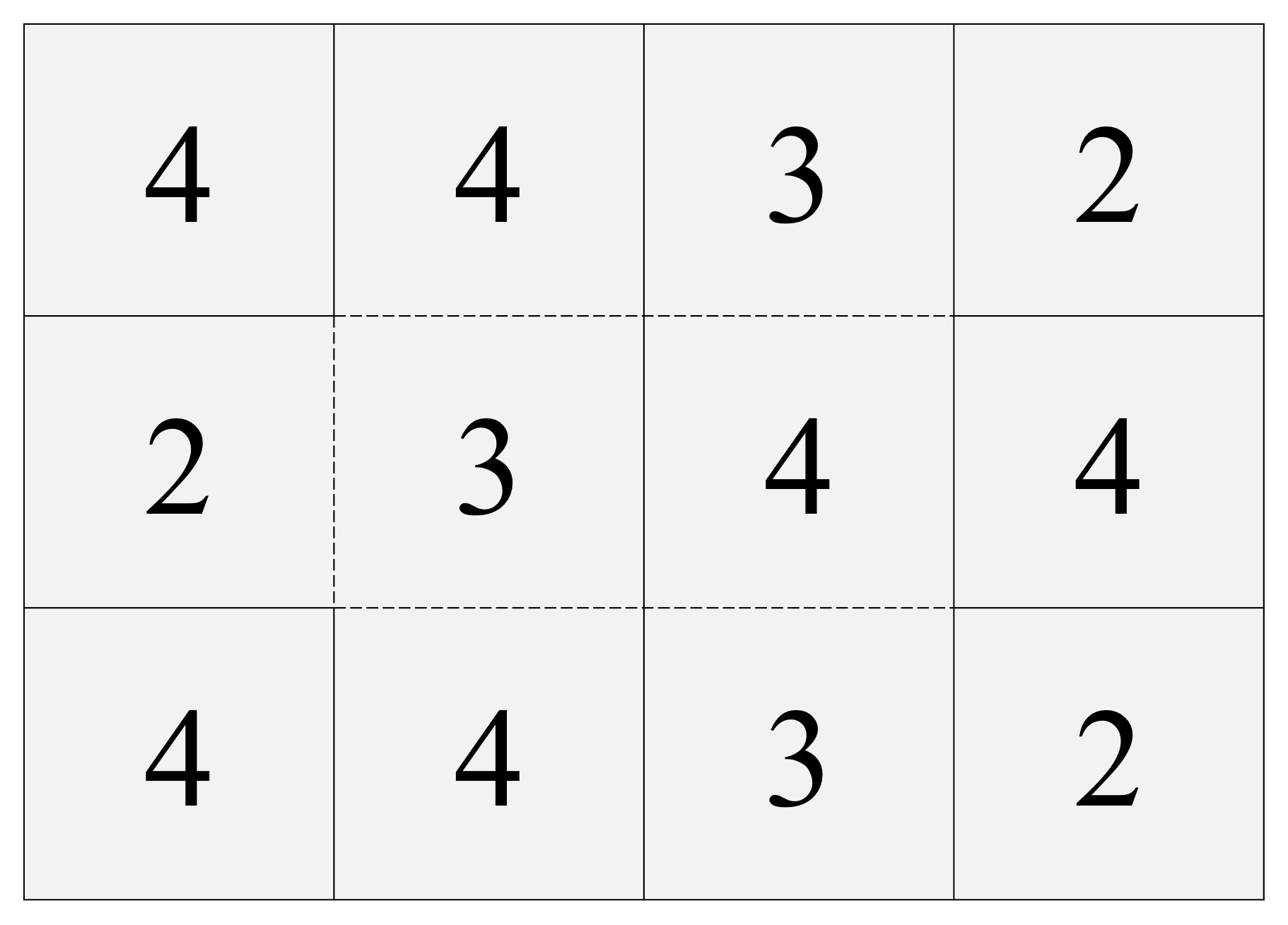
Punto 1. Tomamos la hoja de papel, que colocamos con el lado largo en horizontal, y lo vamos a dividir –por delante y por detrás- en cuatro columnas y tres filas, utilizando líneas trazadas con un lápiz. Generando de esta forma 4 x 3 = 12 casillas rectangulares en cada lado.
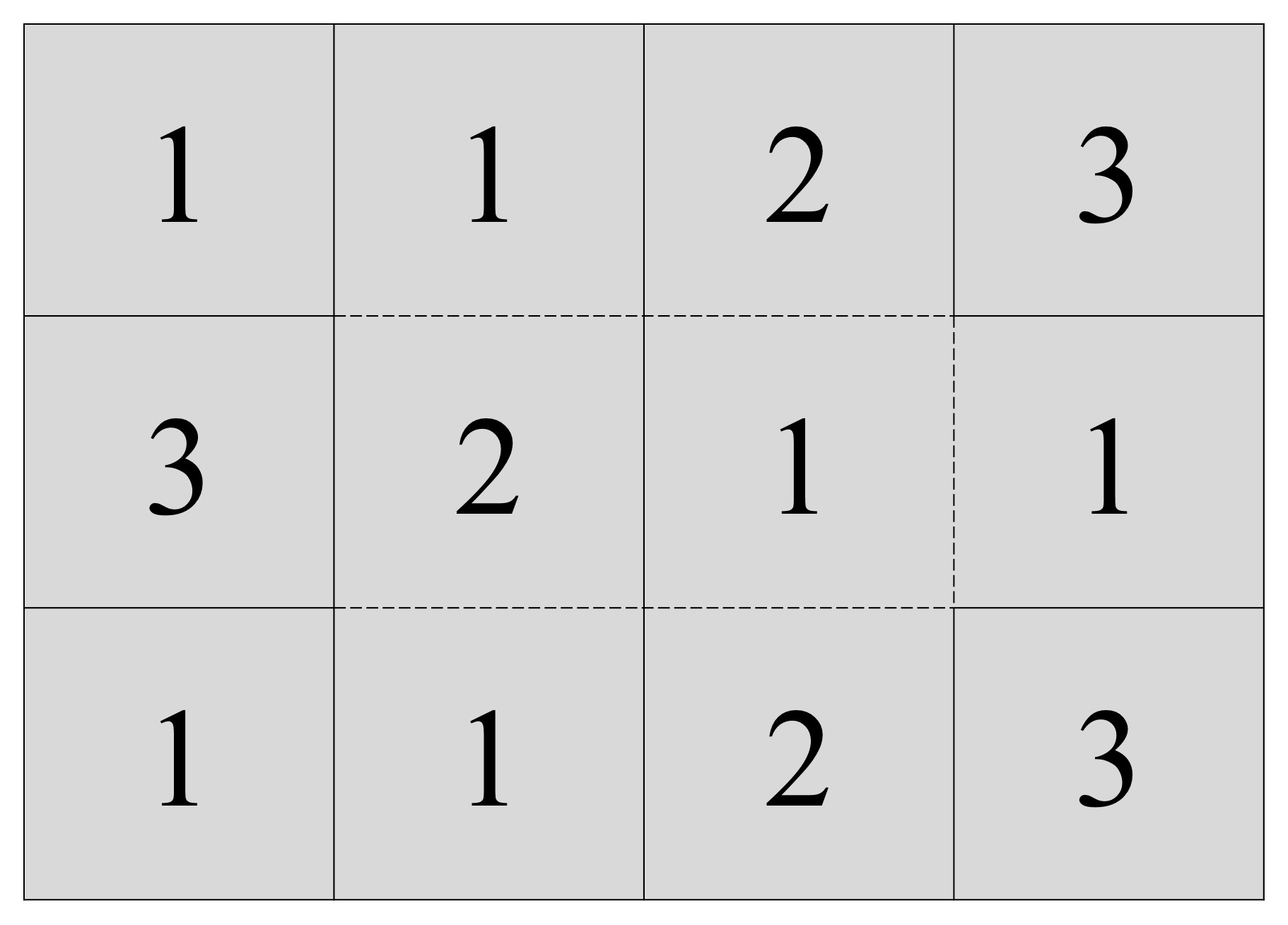
Punto 2. En cada una de las casillas vamos a pintar, centrado, un número. En las 12 casillas de la parte frontal pintamos los números 4, 4, 3, 2 (en la primera fila, la de arriba), luego 2, 3, 4, 4 (en la segunda fila, en medio) y 4, 4, 3, 2 (en la tercera). Ahora en las casillas de la parte trasera pintamos los números 1, 1, 2 y 3 (arriba), 3, 2, 1, 1 (en medio), 1, 1, 2, 3 (abajo). Ojo, aquí quien lo desee puede echarle imaginación y pintar unos números chulos.
Punto 3. Ahora tenemos que realizar un pequeño corte con unas tijeras, por lo tanto, hay que tener cuidado. Si la actividad la realizan niños y niñas pequeños necesitarán la ayuda, o supervisión, de una persona mayor. Antes de realizar el corte, doblad por las líneas rectas que habéis pintado a lápiz, os ayudará a realizar el corte y además es necesario para la parte final.
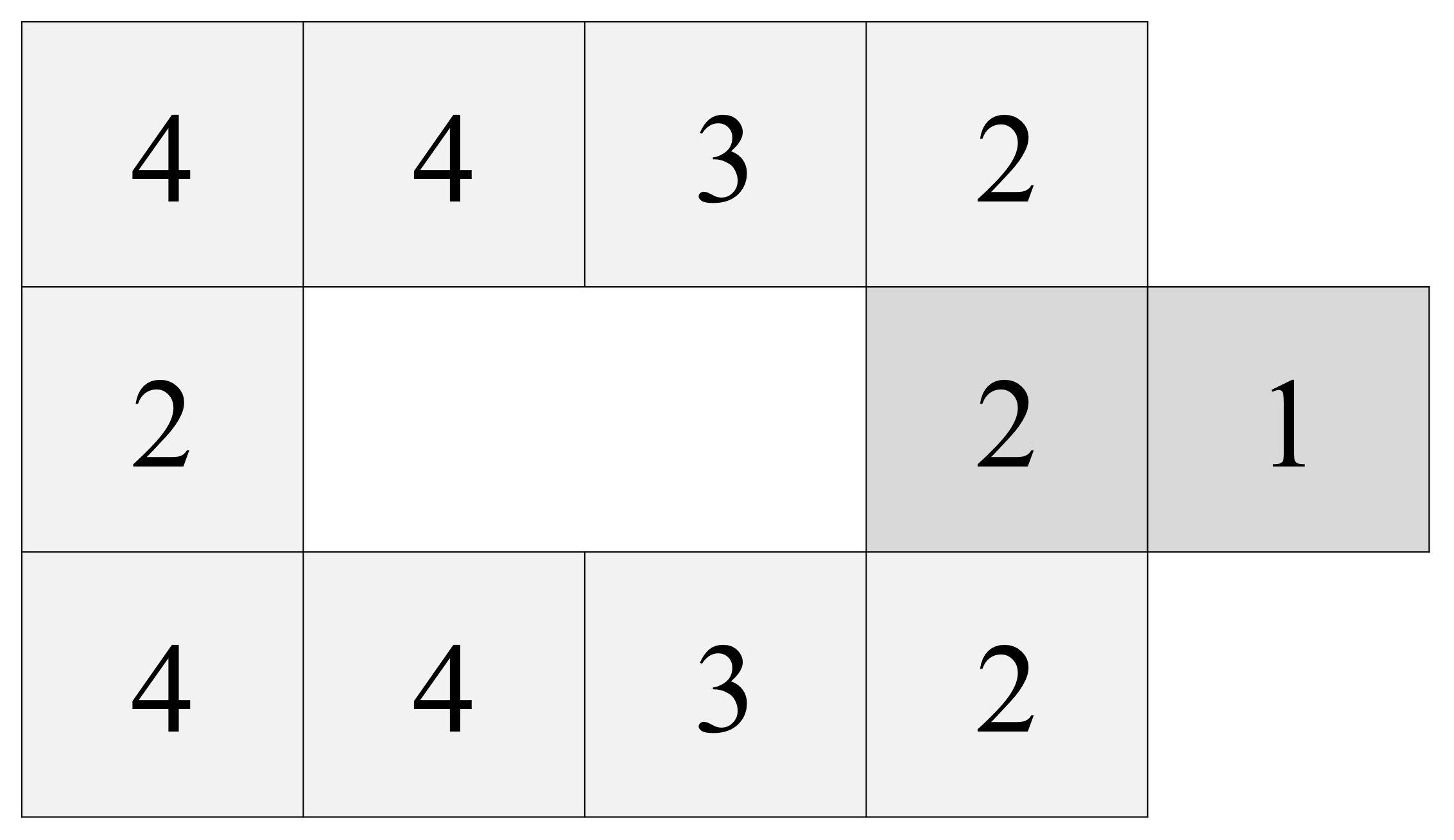
Pero vayamos con el corte. Si consideramos la hoja de papel con la parte frontal, la primera, la que tiene solo doses, treses y cuatros, entonces vamos a cortar el papel para separar las dos casillas del centro –con los números 3 y 4- del resto, pero por todos los lados, salvo uno, el derecho –donde se unen los dos cuatros (véase la siguiente imagen).
Es decir, cortaremos los lados de arriba de las casillas centrales, 3 y 4, el lado izquierdo de la casilla del 3 y los lados de debajo de esas dos casillas centrales. De esta forma, estas dos casillas, 3 y 4, que están unidad entre sí, solo están unidas al resto por el lado derecho, el lado entre los dos cuatros.
Punto 4. A continuación, vamos a realizar unos cuantos dobleces para generar nuestra nueva hoja de papel, que tendrá 2 x 3 = 6 casillas.
Primero, doblamos esa parte central, de dos casillas, hacia la derecha, de forma que va a quedar un 2 hacia arriba, donde estaba el 4, y el 1 que lo acompaña quedará por debajo de la hoja.
Después, doblamos la columna 4, 2, 4 hacia la derecha, una vez, y después toda la nueva columna (sobre la que ahora vemos los números 3, 1, 3) de nuevo hacia la derecha.
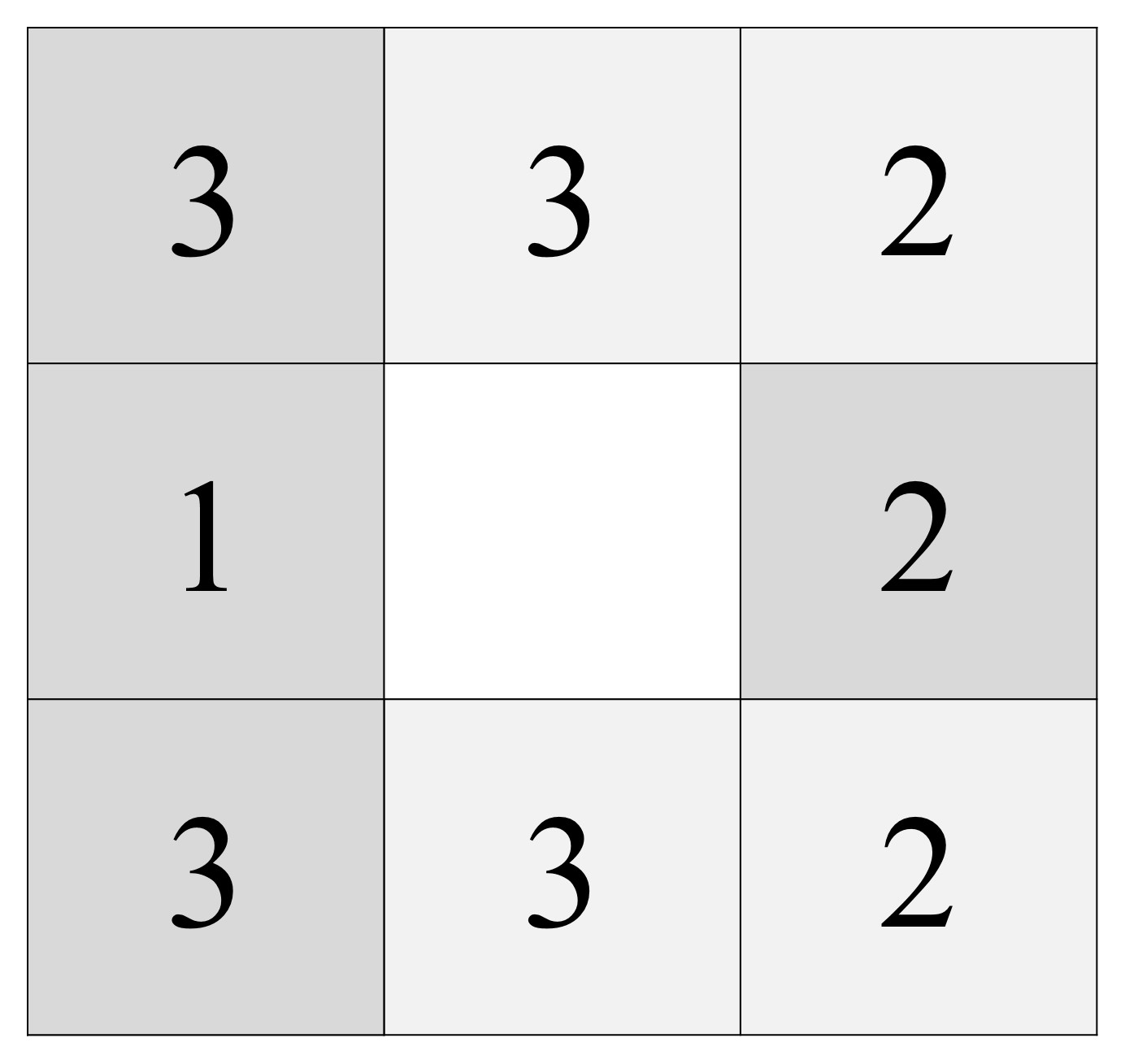
Nos quedará una hoja de papel con 2 x 3 = 6 casillas, con un 2 en todas las casillas, como muestra la siguiente imagen.
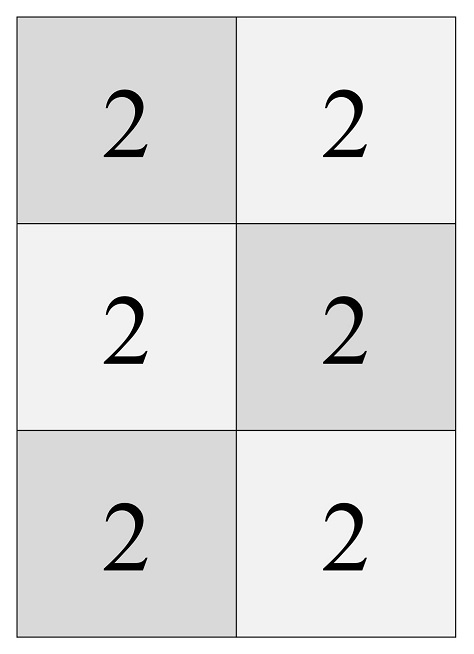
Punto 5. Si le dais la vuelta a la nueva hoja de 6 casillas, tendréis una hoja de papel con un 1 en todas las casillas (la imagen de abajo). Estamos entonces en el último paso. Hay que poner un poco de celo uniendo los dos unos de la fila del centro, el de la izquierda con el de la derecha.
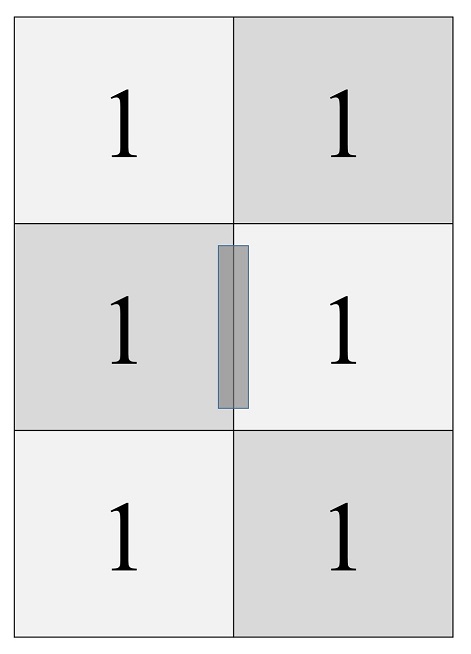
Y ya tenéis la “nueva” hoja de papel con cuatro caras. Veámoslo. En la que tenemos delante solo hay unos (1), le damos la vuelta y solo hay doses (2), luego dos caras. Ahora, con los doses mirando hacia nosotros, doblaremos la hoja por la mitad vertical, llevando las dos mitades hacia atrás, y cuando lleguemos a juntar las dos partes veremos que se nos abre la hoja por el medio, la ayudamos a abrirse con nuestros dedos y veremos que la hoja que tenemos delante tiene todo treses (3).

Si volvemos a doblar la hoja por la mitad vertical, hacia atrás, descubriremos una nueva cara con todo cuatros (4). Es decir, tenemos una hoja de papel con cuatro caras, un tetratetraflexágono. Solo un consejo, antes de mostrárselo a las demás personas practicad el paso de una cara a otra.
La parte básica del taller es la que acabamos de describir arriba, pero a partir de ahí cada cual puede echarle imaginación y hacer el flexágono lo más artístico o curioso que considere oportuno. Por ejemplo, Cristina Barcala, una apasionada de la divulgación científica y lectora del Cuaderno de Cultura Científica, nos mandaba su propia versión, de tamaño mini (la siguiente imagen).

Aunque si os ha gustado esta actividad sobre la realización de un tetraflexágono, podemos abordar la realización de los otros dos tetraflexágonos que aparecen en el artículo Tetraflexagons, del libro de Martin Gardner The 2nd Scientific American Book of Mathematical Puzzles and Diversions (1961), uno de tres caras –tritetraflexágono- y otro de seis caras –hexatetraflexágono-.
Empecemos con el tritetraflexágono. Para realizarlo hay que construir con una hoja de papel una “tira de papel” de dos filas, como la que aparece en la siguiente imagen, trazar las seis casillas de cada cara y dibujar los números 1, 2 y 3 en las casillas, de la parte frontal y trasera, como aparece en la imagen.
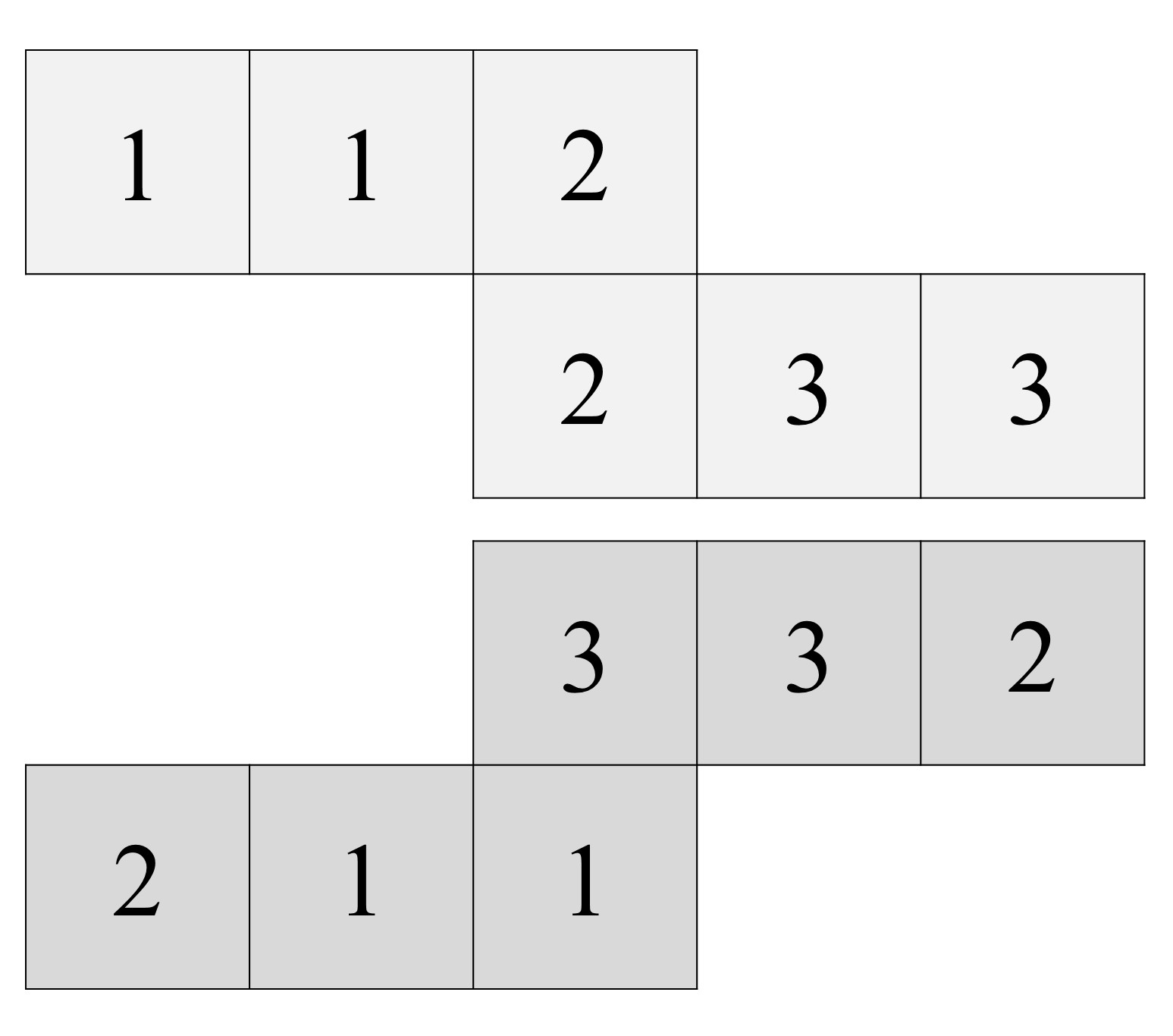
Después doblamos hacia atrás las dos casillas de la izquierda, las que tienen los unos, quedando nuestra tira de papel como se ve en la imagen.
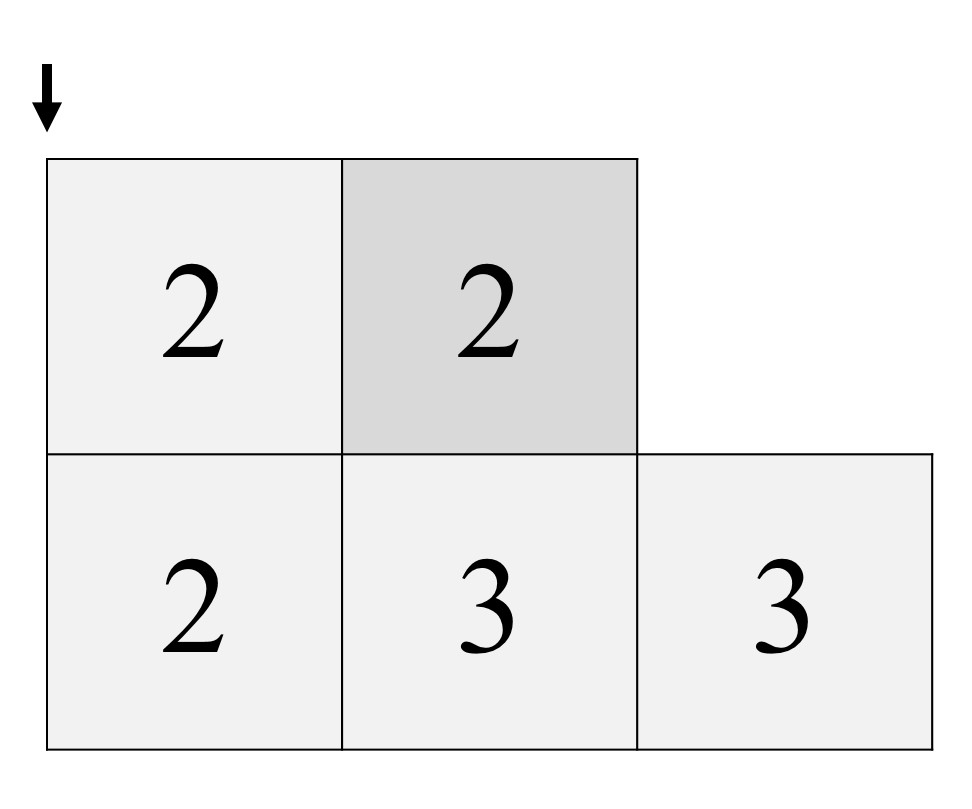
Y doblamos, ahora hacia delante, la casilla de la derecha, la que tiene el tres, quedando así todas las casillas con doses frente a nosotros.
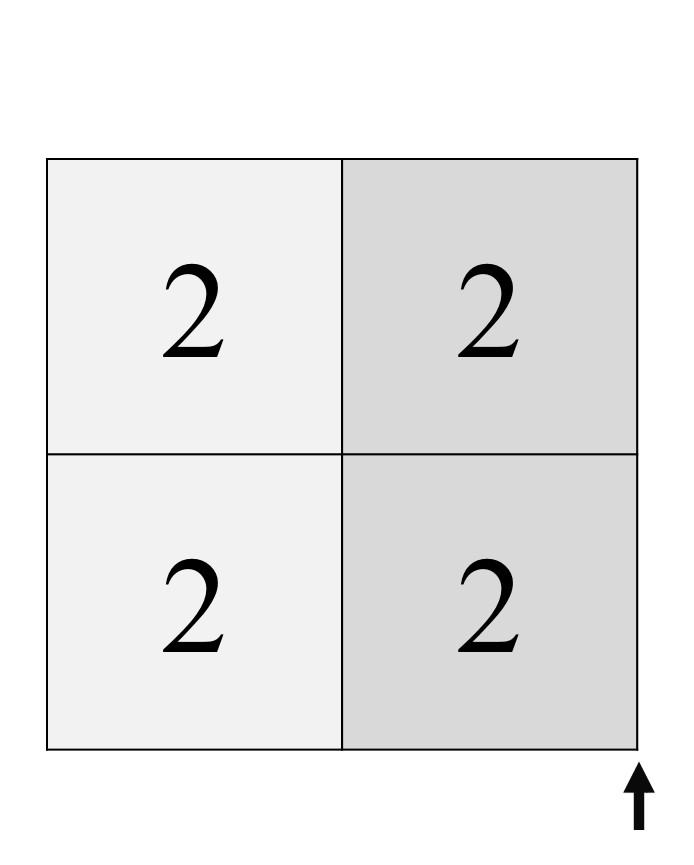
Para finalizar, solo hay que colocar un pequeño trozo de celo entre las dos casillas de la derecha, como se muestra en la imagen.
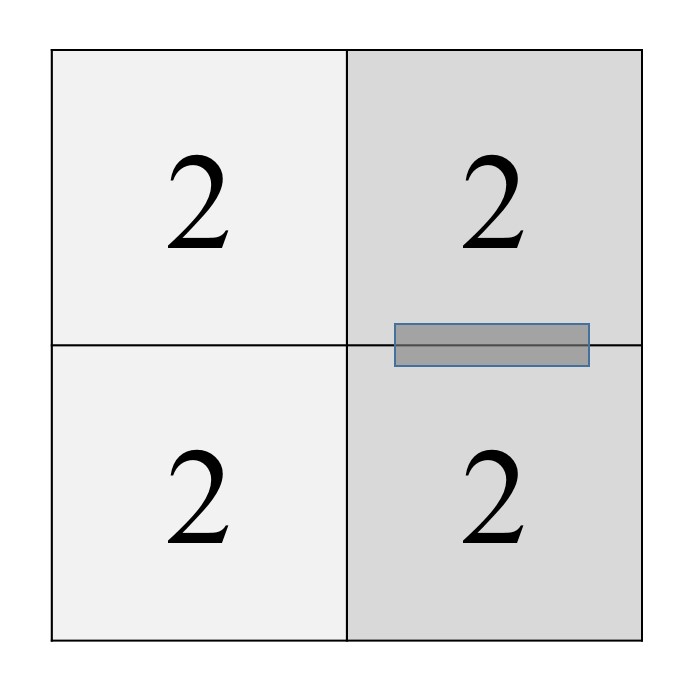
De esta forma, hemos construido el tritetraflexágono, que tiene tres caras, podemos mostrar en cada una de esas caras, todos unos, doses o treses.
Por último, vamos a terminar con los esquemas para realizar el hexatetraflexágono. Para este flexágono, partimos de una hoja cuadrada, dividida en 16 casillas –cuatro filas y cuatro columnas- en cada cara, a la que le hemos cortado las cuatro casillas del centro. Luego solo le quedan las 12 casillas del exterior. Esta vez vamos a utilizar seis colores (aunque mantenemos los números para seguir las instrucciones de la construcción) para pintar cada casilla, de la parte frontal y trasera, como aparece en las siguientes imágenes.
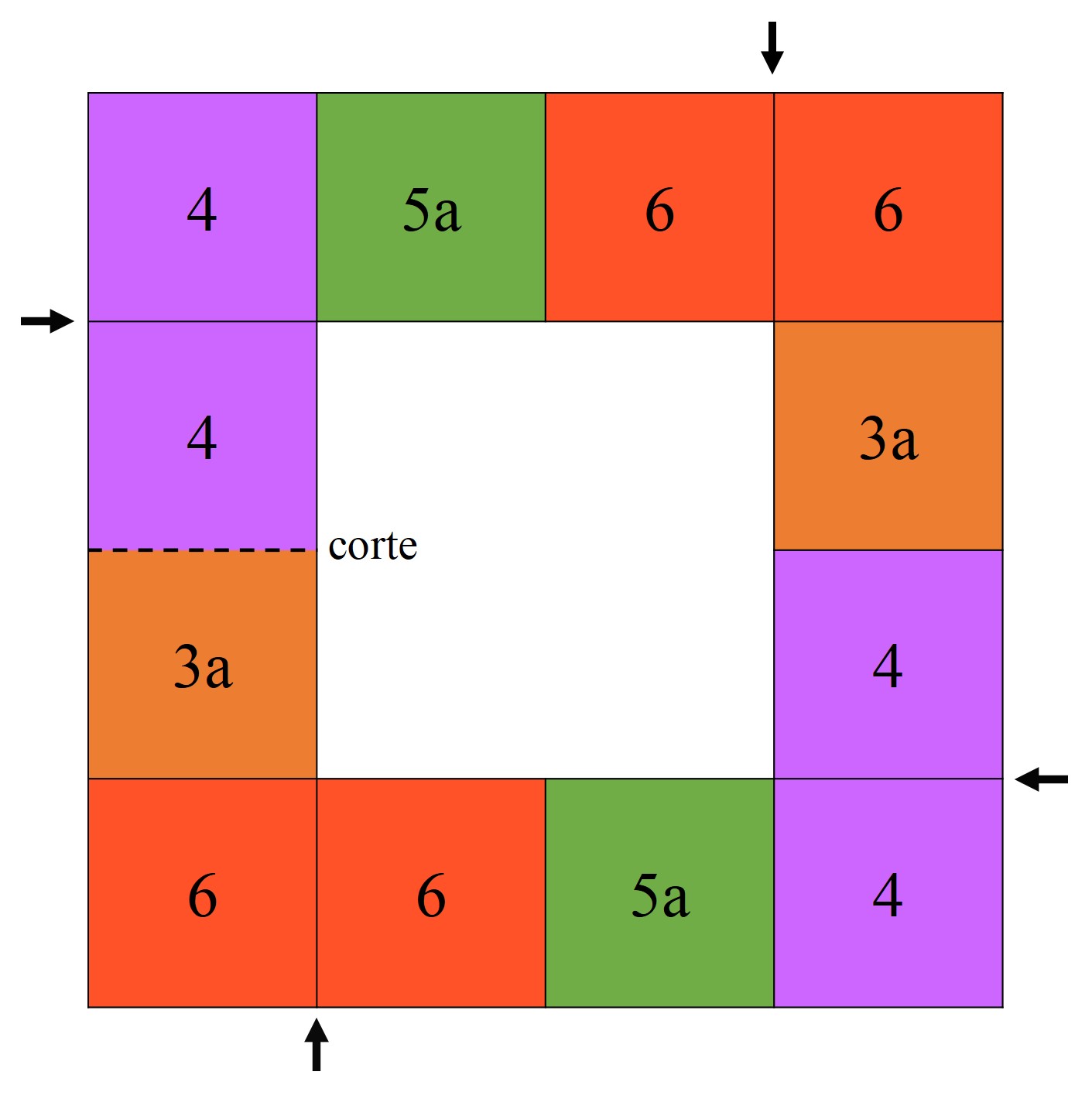
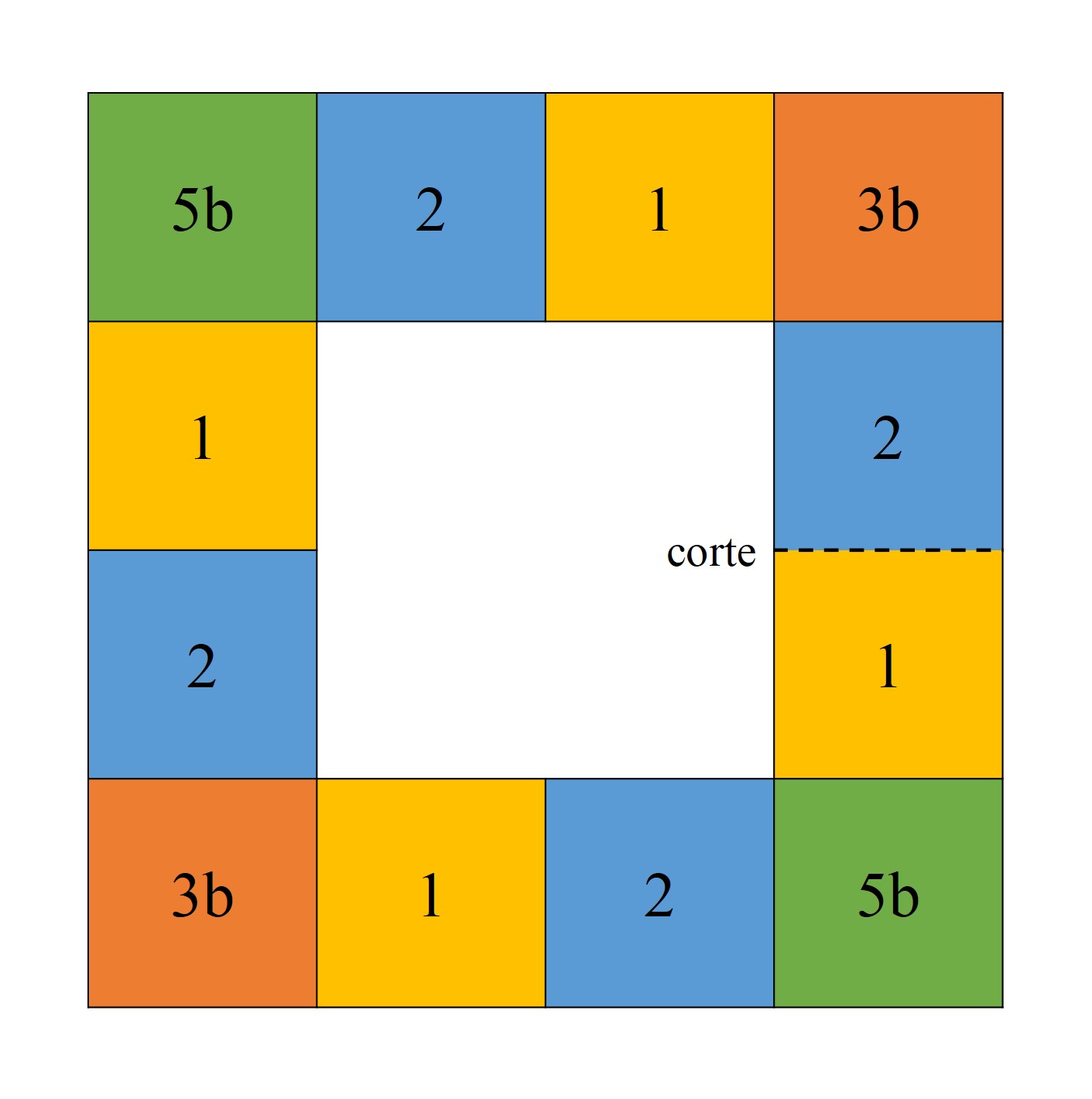
Las dos casillas de la derecha (en la primera imagen) se separan con un pequeño corte horizontal. Entonces, vamos doblando por donde indican las flechas, empezando por la flecha de abajo y en el sentido de las agujas del reloj, de forma que lo que nos queda al terminar es la siguiente imagen.

De nuevo, doblamos por donde indican las flechas, hasta que quede como la siguiente imagen. Para terminar, solamente hay que añadir un trozo de celo para unir, por arriba, la casilla superior izquierda de delante, con la que tiene atrás.

Y ya tendríamos nuestro hexatetraflexágono.
Bibliografía
1.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987 (publicado originalmente en 1961).
2.- Robert Ghattas, Bricológica, Treinta objetos matemáticos para construir con las manos, RIALP, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Lo Mejor de la Semana (19 – 25 de abril) | Hablando de Ciencia
[…] La hoja de papel de cuatro caras, una propuesta de taller. En estos tiempos de confinamiento, nada mejor para pasar el tiempo que construir este curioso objeto matemático popularizado en su día por Martin Gardner. […]