Los triángulos son los polígonos más simples, pero los más especiales. Aprendemos en la escuela a temprana edad sus mágicas propiedades, como por ejemplo que sus ángulos siempre suman 180 grados o el famoso teorema de Pitágoras, que se cumple si uno de los tres ángulos es recto. Estas sencillas peculiaridades pueden aplicarse al mundo real y ayudarnos a comprender mejor cómo funcionan las cosas.

Relatividad especial
La conocida teoría de la relatividad especial de Albert Einstein relaciona el tiempo y el espacio, y da lugar a llamativas consecuencias físicas. Entre ellas, las más mencionadas son la dilatación del tiempo, la contracción de la longitud o el aumento de la energía que podemos medir, si un objeto se desplaza a cierta velocidad con respecto a nosotros. Todo esto parece muy complicado, pero puede expresarse mediante un simple triángulo rectángulo.
La velocidad por el tiempo es igual a la distancia. Si tenemos un láser y un detector colocados a cierta distancia como vemos en la Figura 1, podemos detectar el instante t en el que llega la luz al extremo superior. Como la velocidad de la luz es c, la distancia recorrida es c por t.
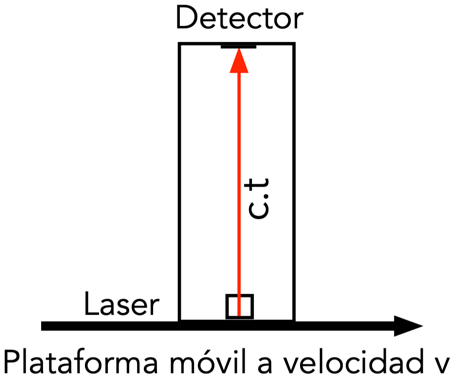
Si, como aparece en la Figura 1, montamos el láser en una plataforma que se mueve a velocidad v, pero en dirección perpendicular a como apuntamos el láser, podemos repetir el experimento, pero esta vez observándolo desde fuera de la plataforma. Como se muestra en la Figura 2, desde fuera veremos un recorrido diagonal del láser, debido a la composición del movimiento vertical y horizontal que percibimos desde el exterior. Como la velocidad de la luz es siempre c, la distancia diagonal recorrida por el láser que vemos desde fuera es c por t’. Finalmente, el tercer lado del triángulo de la Figura 2 es el recorrido horizontal de la plataforma (v por t’).
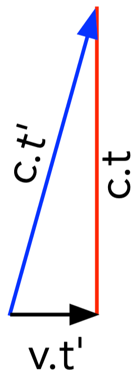
Tenemos un triángulo rectángulo, así que podemos aplicar el teorema de Pitágoras: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Con este simple cálculo extraemos de este triángulo las transformaciones de Lorenz, que son las fórmulas que nos cuantifican cuánto se dilata el tiempo o se contrae la longitud, si un objeto se mueve a una velocidad v respecto a nosotros. Este factor se llama factor de Lorenz γ. Si llamamos β a la razón entre una velocidad v y la máxima velocidad posible (la velocidad de la luz en el vacío c) podemos construir otro triángulo rectángulo como mostramos en la Figura 3:
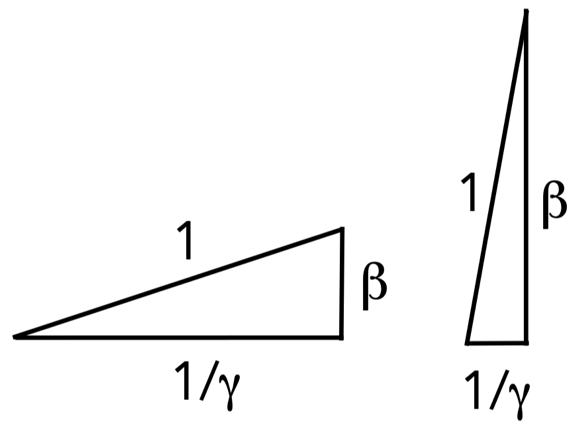
Aplicando de nuevo el teorema de Pitágoras podemos fácilmente calcular cuánto se modifican las medidas del tiempo y la longitud cuando los objetos se mueven a mayor o menor velocidad. Vemos por ejemplo que si β es pequeña (bajas velocidades, a la izquierda de la Figura 3), 1/γ es ligeramente menor que 1 y. por tanto, γ es ligeramente superior a 1, con lo cual las medidas del tiempo y longitud apenas se modifican. Para velocidades altas (a la derecha de la Figura 3), 1/γ es muy pequeño, con lo que el factor de Lorenz γ es muy grande, y se produce un gran efecto.
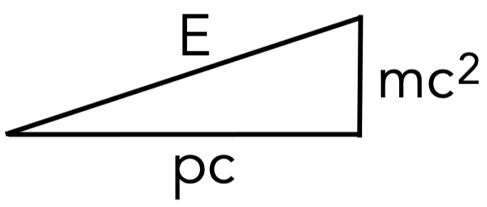
Una de las consecuencias más llamativas de la relatividad especial es la relación energía-momento, que se utiliza en todas partes, desde la mecánica cuántica hasta la relatividad general. Una vez más el teorema de Pitágoras nos permite cuantificar la energía de un objeto de cierta masa y de cierta cantidad de movimiento (momento o ímpetu p). Este triángulo mostrado en la Figura 4 nos permite calcular la energía de cualquier objeto móvil, incluso aquellas partículas sin masa, como los fotones, que viajan a la velocidad de la luz, cuyo cateto derecho de la Figura 4 es nulo, o un objeto inmóvil, cuyo cateto inferior en la Figura 4 sería nulo, pero su energía sería igual a la famosa equivalencia de masa y energía de Einstein E=mc2.
Energía eléctrica
La mayoría de los generadores de electricidad son máquinas rotatorias, como un aerogenerador (“molino” de viento), un salto de agua de un embalse, que mueve las turbinas de una central hidroeléctrica, o el vapor de agua que se produce en una central nuclear o en una térmica, que también actúa sobre sus turbinas de vapor, que giran y generan electricidad.
Al ser máquinas rotatorias, la electricidad que se produce es de corriente alterna. Las señales alternas se expresan de forma compacta en matemáticas con números complejos, lo cual a veces parece algo muy complicado de entender, pero de nuevo aparecen los sencillos triángulos para representar gráficamente la tensión (voltios), la corriente (amperios) y la impedancia (ohmios) de cualquier circuito eléctrico.
La potencia eléctrica que nos da un suministrador es el producto de la tensión por la corriente eléctrica que circula cuando enchufamos un aparato. Resulta que si medimos los voltios y los amperios alternos que circulan, puede ser que estas oscilaciones no se produzcan a la vez, sino que la corriente esté ligeramente desfasada con respecto a la tensión. Este desfase se representa en la Figura 5 mediante el ángulo φ del triángulo mostrado. Este triángulo nos indica que si el desfase φ es grande, no aprovechamos bien la electricidad generada y transportada. En trigonometría el coseno de un ángulo pequeño es cercano a 1, y el cosφ es el conocido factor de potencia eléctrica, que cuanto más cerca esté de 1, más eficiente resulta el circuito.
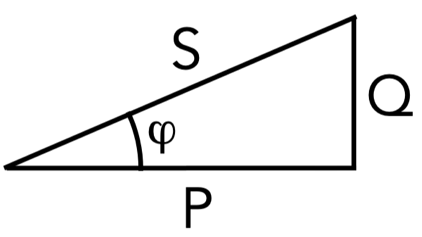
El desfase φ se produce típicamente por la gran cantidad de cableados y bobinados que son necesarios para generar, transformar y transportar la energía eléctrica. Para mejorar la eficiencia podemos contrarrestar el desfase en este caso mediante un conjunto de condensadores eléctricos para regular φ hacia valores mínimos y mejorar el factor de potencia.
Medida del radio de la tierra
Eratóstenes de Cirene (276-194 a.e.c.) fue uno de los sabios de la antigüedad que más conocimiento pudo adquirir y aplicar, al hacerse cargo de la Biblioteca de Alejandría durante más de 40 años. Entre sus muchas contribuciones a la ciencia, la maravillosa criba de Eratóstenes, sencillo algoritmo para obtener números primos y la medida del radio de la Tierra con instrumental rudimentario son, en mi opinión, sus más alucinantes aportaciones, por la importancia de sus resultados aplicados, la simplicidad de su realización y la potencia de su razonamiento.
No sabemos con todo detalle cómo midió Eratóstenes el radio de la Tierra, ya que no nos han llegado sus escritos directos, sino lo narrado por otros autores. Así todo, es brillante su observación de que el solsticio de verano, el sol al mediodía no arrojaba sombra en los pozos de Siena (hoy Asuán), y, sin embargo, en su ciudad, Alejandría, los árboles, obeliscos o palos verticales sí que proyectaban sombra de longitud medible.
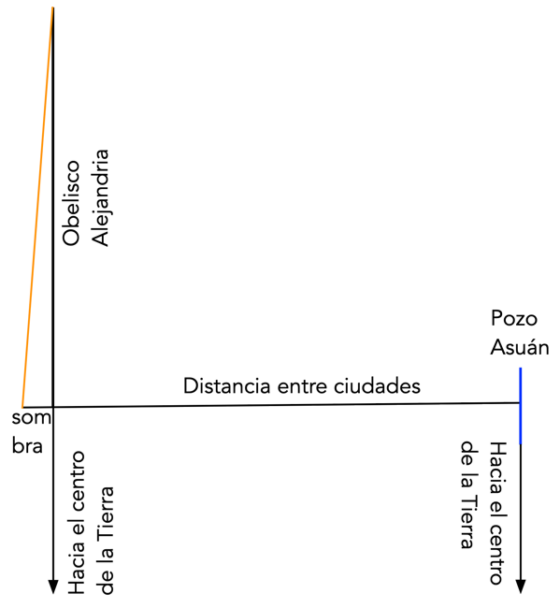
Si Eratóstenes utilizó alguno de los antiguos obeliscos de Alejandría, de una altura aproximada de 21 metros, pudo medir una sombra bien mensurable de unos 2,6 metros. Sus colaboradores o los datos de la Biblioteca le dieron una medida de distancia entre las ciudades de Asuán y Alejandría de aproximadamente 800 kilómetros (ver Figura 6).
El cálculo de Eratóstenes suele narrarse con cierta exactitud geométrica, al aplicar el quinto postulado de Euclides, de Los Elementos, que con seguridad se hallaba presente en la Biblioteca de Alejandría. Este postulado equivale a que los ángulos de cualquier triángulo suman 180 grados, o también que, si dos rectas son paralelas, los ángulos alternos internos formados con otra recta que corta a ambas son iguales. Sin embargo, resulta muy complicado medir con exactitud un ángulo tan pequeño como el de los rayos del sol proyectando sombra en Alejandría, ya que Eratóstenes no disponía entonces de cálculo trigonométrico.
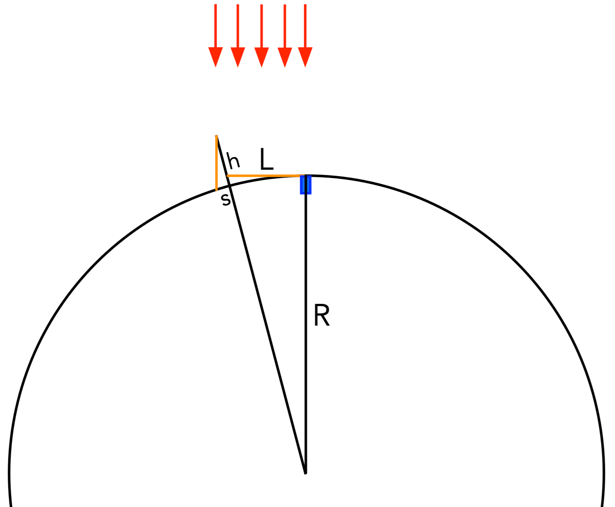
Para evitar un cálculo fino de 7,2 grados, y, por tanto, el ángulo del sector terrestre que separa ambas ciudades, en la Figura 7 se muestra un posible cálculo no exacto, pero sí sencillo, que es plausible Eratóstenes pudo haber usado para obtener el radio de la Tierra. Se trata de dos triángulos semejantes. Tenemos bien medidos los dos catetos del triángulo pequeño del obelisco, y aproximadamente medido el cateto pequeño del triángulo grande, que es la distancia entre ambas ciudades. Esta distancia curva entre ciudades es solo ligerísimamente inferior a la longitud L mostrada en la Figura 7, de modo que la magia de dos triángulos semejantes permitiría a Eratóstenes efectuar una simple regla de tres, y el radio de la Tierra es R=L(h/s), es decir R = 800 km (21 m/2,6 m) = 6461 km. Los triángulos son asombrosos.
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)

Marcelo Saina
En mis 86 años lamentablemente he podido apreciar el tobogán del interés por el conocimiento profundo, y mucho me complace el haber hallado este rincón en el cual todavía puede abrevar nuestra sed de saber MÁS. Gracias.