A finales del siglo XIX, el matemático ruso-alemán Georg Cantor (1845-1918) conmocionó al mundo de las matemáticas, rompiendo las creencias existentes sobre el concepto de infinito. Entre los revolucionarios resultados que demostró están que existe más de un infinito o que la cantidad de puntos de un segmento es la misma que la cantidad de puntos de un cuadrado. A esta revolución matemática hemos dedicado, en el Cuaderno de Cultura Científica, la miniserie titulada El infinito en un segmento.

La primera entrega de esta miniserie, El infinito en un segmento (1), se centró en cómo resolvió el matemático ruso-alemán el problema de comparar dos conjuntos con infinitos elementos. La respuesta es sencilla y está en la base del origen del concepto de número. Dos conjuntos tienen la misma cantidad de elementos cuando se puede establecer una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos. De esta forma, llegamos a la paradoja de que para un conjunto infinito existen subconjuntos propios del mismo que tienen la misma cantidad de elementos que el propio conjunto. Por ejemplo, el conjunto de los números pares tiene la misma cantidad de elementos que el conjunto de los números naturales (que está formado por los números pares y los números impares).

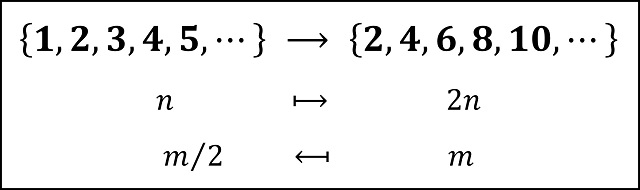
De hecho, Georg Cantor tomó esta paradoja del ininfito como definición de “conjunto infinito”, es decir, un conjunto es infinito si existe un subconjunto propio suyo que tiene la misma cantidad de elementos que el conjunto.

En esta primera entrega de la serie se demostró también que los conjuntos de los números enteros y de los números racionales son conjuntos numerables, es decir, tienen la misma cantidad de elementos que el conjunto de los números naturales.

En la segunda entrega de esta miniserie, El infinito en un segmento (2), se mostró que el conjunto de los números reales (de forma explícita, en la demostración se consideró el intervalo (0,1), es decir, los números reales entre 0 y 1) no es numerable, no se puede poner en correspondencia uno-a-uno con los números naturales. Por lo tanto, existe más de un infinito, al menos, el infinito de los números naturales (cuyo cardinal se denomina aleph-zero) y el infinito de los números reales (cuyo cardinal se denomina cardinal del continuo, c).

El infinito en un cuadrado

Como se comentó al final de la segunda entrada de esta miniserie, una vez demostrado que el cardinal del continuo c (el infinito de los números reales) es mayor que aleph-zero (el infinito de los números naturales), Georg Cantor se planteó si el plano (de dimensión 2) tiene una mayor cantidad de puntos que la recta (de dimensión 1), es decir, si el infinito del plano es mayor que el infinito del continuo. Simplificando la cuestión.

Problema: ¿Hay la misma cantidad de puntos en el segmento unidad [0,1] que en el cuadrado unidad [0,1] x [0,1]?

Para abordar el anterior problema, primero recordemos un par de cuestiones básicas. La primera es que los números reales del intervalo [0,1], es decir, mayores que 0 y menores que 1, se escriben en forma decimal como

donde, si todos los dígitos son 0 se obtendría el número cero (0), y si todos los decimales son 9 se obtendría el número uno (1), ya que, como se comentó en la anterior entrada, el número 1 se puede representar de dos formas distintas 1,00000000… (infinitos ceros) y 0,99999999… (infinitos nueves). Por ejemplo, el número pi menos 3, que es un número real del intervalo (0,1) se expresa como 0,1415926535…

La segunda cuestión básica es que todo elemento del plano real se puede identificar con sus coordenadas cartesianas, es decir, con un par (x, y), donde x e y son números reales, como se muestra en la siguiente imagen (aunque en ella solamente se han utilizado puntos cuyas coordenadas x e y son números enteros).

De manera, que los elementos del cuadrado [0,1] x [0,1], serán los puntos del plano (x, y), donde x e y son números reales del intervalo [0,1]. Es decir, son de la forma

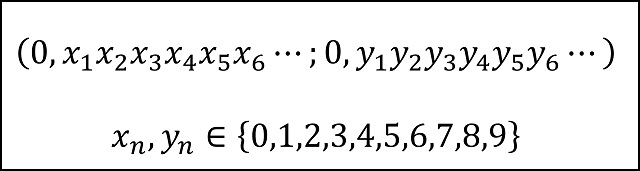
Ahora, una cuestión técnica. Antes de entrar en la construcción de la buscada correspondencia uno-a-uno entre el segmento y el cuadrado, vamos a tener en cuenta lo siguiente, de cara a dicha construcción. Como se puede demostrar (aunque no quiero meterme ahora en esta cuestión para no complicar más esta entrada) que los segmentos [0,1], es decir, los números reales mayores o iguales que 0 y menores o iguales que 1; (0,1], es decir, los números reales mayores que 0 y menores o iguales que 1; y (0,1), es decir, los números reales mayores que 0 y menores que 1, tienen la misma cantidad de elementos (existen correspondencias uno-a-uno entre ellos), es equivalente demostrar que existe una correspondencia uno-a-uno entre el segmento [0,1] y el cuadrado [0,1] x [0,1], que entre el segmento (0,1] y el cuadrado (0,1] x (0,1] o que entre el segmento (0,1) y el cuadrado (0,1) x (0,1). Por motivos técnicos, nosotros vamos a centrarnos en construir una correspondencia uno-a-uno entre el segmento (0,1] y el cuadrado (0,1] x (0,1], es decir, los puntos (x, y) tales que sus coordenadas x e y pertenecen a (0, 1].

Por lo tanto, ya estamos en condiciones de mostrar la construcción de Georg Cantor de la correspondencia uno-a-uno entre los elementos del segmento (0,1] y los elementos del cuadrado (0,1] x (0,1], que prueba que ambos conjuntos tienen la misma cantidad de elementos. La idea básica es asignar a cada elemento A del intervalo (0,1], es decir, un número real con su expresión decimal (por ejemplo, 0,1234567891011…), un elemento (B, C) del cuadrado (0,1] x (0,1] tal que los decimales de la primera coordenada B son los decimales en las posiciones impares de A y los decimales de la segunda coordenada C son los decimales en posiciones pares de A, como se muestra en la imagen.

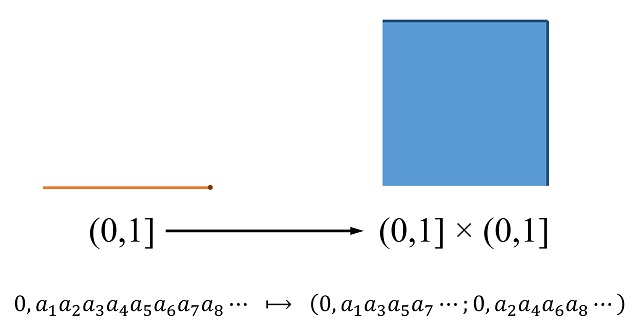
Y cuya aplicación inversa, es decir, que envía los elementos del cuadrado (0,1] x (0,1] en elementos del segmento (0,1], está definida mediante la construcción inversa, juntando los decimales de ambas coordenadas e intercalándolos en posiciones impares y pares.

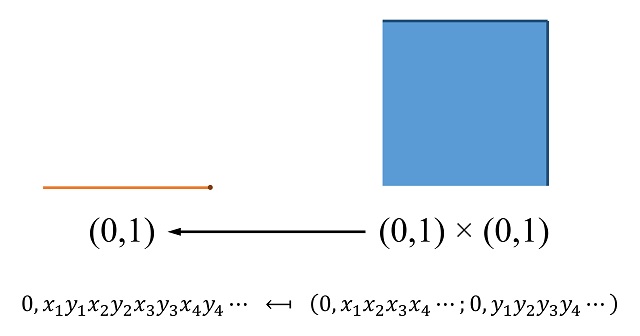
Por ejemplo, la imagen de la conocida “constante de Champernowne”, que es el número real, entre 0 y 1, cuyos decimales son los números naturales ordenados de izquierda a derecha, es decir,

0,123456789101112131415161718192021…

es el punto del cuadrado (0,1] x (0,1] cuyas coordenadas son

(0,135790123456789012…; 0,24681111111111222…).

Por otra parte, si tomamos el punto del cuadrado (0,1] x (0,1] dado por las coordenadas (x, x), donde x es la raíz de 2 menos 1, es decir, el punto

(0, 41421356237309…; 0, 41421356237309…),

su imagen, mediante la aplicación inversa, es el elemento del segmento (0,1] dado por la siguiente expresión

0, 4411442211335566223377330099…

Resolviendo algunas cuestiones técnicas

La idea de Cantor es ingeniosa, sin embargo, el hecho de que haya números reales, en concreto, los números racionales con un número finito de decimales (incluido en caso en el que no hay decimales, es decir, los números enteros) que tienen dos representaciones genera algunos problemas en la anterior aplicación, que hay que resolver.

Problema 1. Como decíamos, hay números que tienen dos representaciones decimales, por ejemplo, el número racional 11/20 se puede representar como 0,55 (o si lo preferimos 0,55000000…) y 0,54999999… Esto es un problema, ya que ese número racional tendría dos posibles imágenes mediante la anterior construcción

(0,500000…; 0,500000…) y (0,599999…; 0,499999…).

Por lo tanto, lo que hizo Cantor fue quedarse con una única representación de las dos, la que tiene infinitos nueves, en este caso, 0,54999999… De esta forma, solo existe, a priori, una imagen en (0,1] x (0,1] de cada número real de (0,1], que, en el ejemplo anterior, es (0,599999…; 0,499999…).

Problema 2. Pero al elegir una única representación de las dos se genera un problema añadido, ya que puede haber números reales de (0,1] cuya imagen contenga una expresión de las primeras y ya no sea válida, como 118/275 = 0,429090909…, cuya imagen sería, por la construcción de Cantor, el punto del cuadrado (0,49999…; 0,20000…), que ya no es un punto válido puesto que para el número 0,2 se ha elegido la representación 0,199999… Notemos que si se admitiesen aquí las dos representaciones se tendría que dos números reales distintos 0,429090909… y 0,4199999999… tendrían la misma imagen (0,49999…; 0,20000…) = (0,49999…; 0,19999…), es decir, la correspondencia no sería uno-a-uno.

Este nuevo problema lo resuelve Cantor de una forma ingeniosa. En la aplicación del segmento (0,1] en el cuadrado (0,1] x (0,1], en lugar de separar dígitos en posiciones pares e impares (y en la aplicación inversa intercalar los dígitos de las dos coordenadas del punto), lo que propone es separar (respectivamente, intercalar) grupos de dígitos, de manera que los ceros consecutivos dentro de la representación decimal se “pegan” al siguiente dígito no nulo. Por ejemplo, los grupos de dígitos de 118/275 = 0,429090909… serían

4 / 2 / 9 / 09 / 09 / 09 …

Por lo tanto, su imagen mediante la aplicación de Cantor sería ahora

(0,49090909…; 0,2090909…).

De hecho, el punto (0,49090909…; 0,2090909…) sería el único punto de (0,1] x (0,1] cuya imagen es 118/275 = 0,429090909…

Veamos otro ejemplo. El número real 0,01002000300004000005… tendría los siguientes grupos de dígitos

01 / 002 / 0003 / 00004 / 000005 …

por lo que su imagen sería el punto del cuadrado de coordenadas (0,010003000005…; 0,002000040000006…). Y ese punto del cuadrado es el único cuya imagen inversa es el número real 0,01002000300004000005…

Por supuesto, los números que no tienen ceros entre sus decimales funcionan como antes. Así, 1/2 = 0,4999999… tiene como imagen (0,4999999…, 0,9999999) y este punto es el único cuya imagen inversa es 1/2 = 0,4999999…

En conclusión, Cantor demostró que existen tantos puntos en el intervalo (0,1], como en el cuadrado (0,1] x (0,1].

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.

2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.

3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis, Undergraduate Texts in Mathematics, Springer, 2013.

4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.

5.- José A. Prado-Bassas, Historia del infinito (el apasionante relato de uno de los conceptos más profundos y enigmáticos de las matemáticas), Pinolia, 2023.

6.- Erich Kamke, Theory of Sets, Dover, 1950.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica