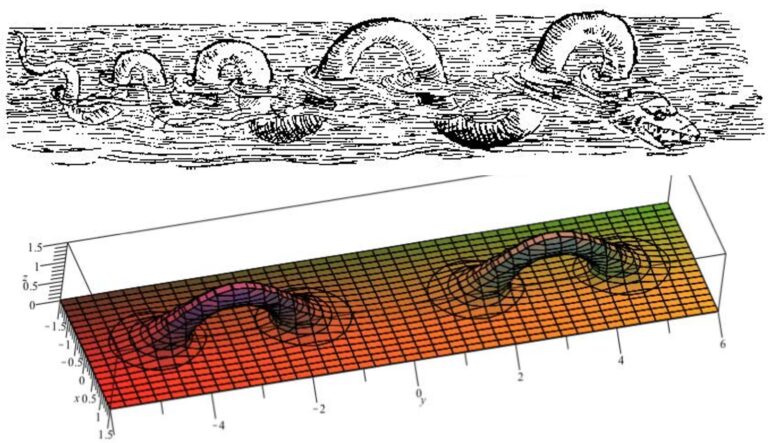
El monstruo del lago Ness existe (al menos en matemáticas)
En la entrada Clasificando en topología: de lo local a lo global recordábamos un hermoso teorema de clasificación:
Toda superficie compacta (cerrada y acotada) y conexa (de una pieza) es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.
Superficies no compactas
La clasificación de superficies no compactas (superficies no cerradas o no acotadas) es mucho más compleja. El enunciado del teorema de clasificación envuelve conceptos parecidos al del caso compacto y una nueva noción, la de final de un espacio topológico.
Esta clasificación la estableció Ian Richards en un celebrado artículo publicado en 1962; involucra los siguientes conceptos explicados de manera muy intuitiva:
-
la “cantidad” de toros o planos proyectivos que posee la superficie (su género). En el caso de superficies no compactas esa “cantidad” puede ser infinita;
-
la “clase de orientabilidad” de la superficie, es decir, la existencia (o la falta de ella) de planos proyectivos en su expresión; y
-
los finales de la superficie, que pueden entenderse como las maneras (topológicas) de moverse hacia el infinito dentro del espacio. El espacio de finales se dota de una topología que expresa precisamente la “dinámica topológica” que posee la superficie (y que la caracteriza).
El concepto de final se puede introducir para cualquier espacio topológico. La definición no es sencilla, por ello damos unos cuantos ejemplos para entenderla mejor.
-
Un espacio compacto no posee finales.
-
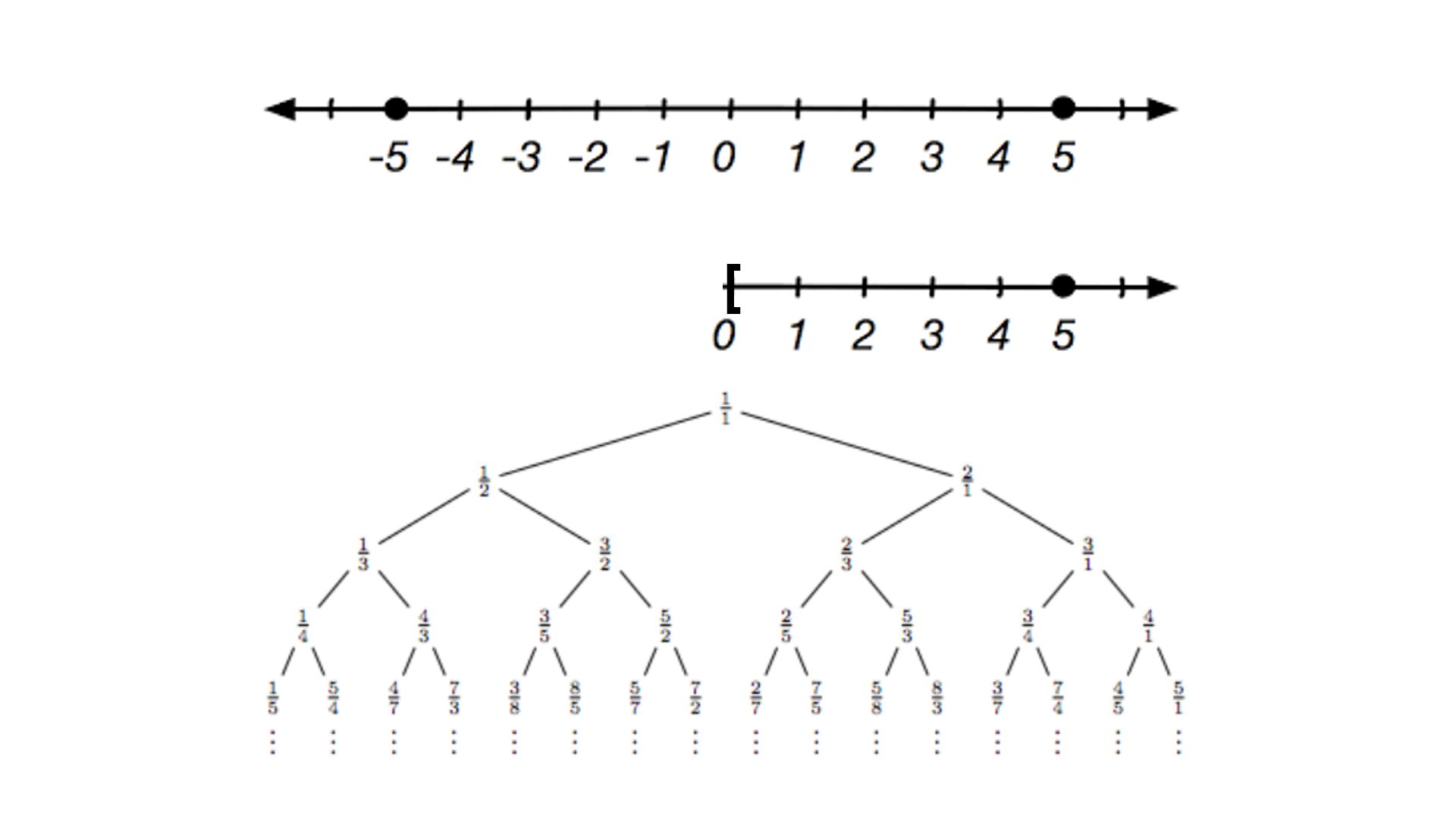
La recta real posee dos finales; son las dos maneras de acercarse al infinito, -∞ o +∞).
-
El intervalo [0, +∞) posee un único final. Aunque es más difícil de visualizar, el plano también posee un único final, así como todos los espacios euclideos de dimensión mayor o igual a 2.
-
Un árbol binario completo infinito posee una cantidad infinita (no numerable) de finales que corresponden a la cantidad infinita de caminos descendentes diferentes que comienzan en la raíz. De hecho, se puede demostrar que el conjunto de finales es homeomorfo al conjunto de Cantor.
Veamos algunos ejemplos de superficies no compactas.
El plano
Es una superficie no compacta con un final y género cero. Es homeomorfa a una esfera (que es una superficie compacta) a la que se ha quitado un punto.
El cilindro
Es una superficie (es el producto de la circunferencia por la recta) no compacta con dos finales y género cero. Es homeomorfa a una esfera a la que se han quitado dos puntos.
El monstruo del lago Ness
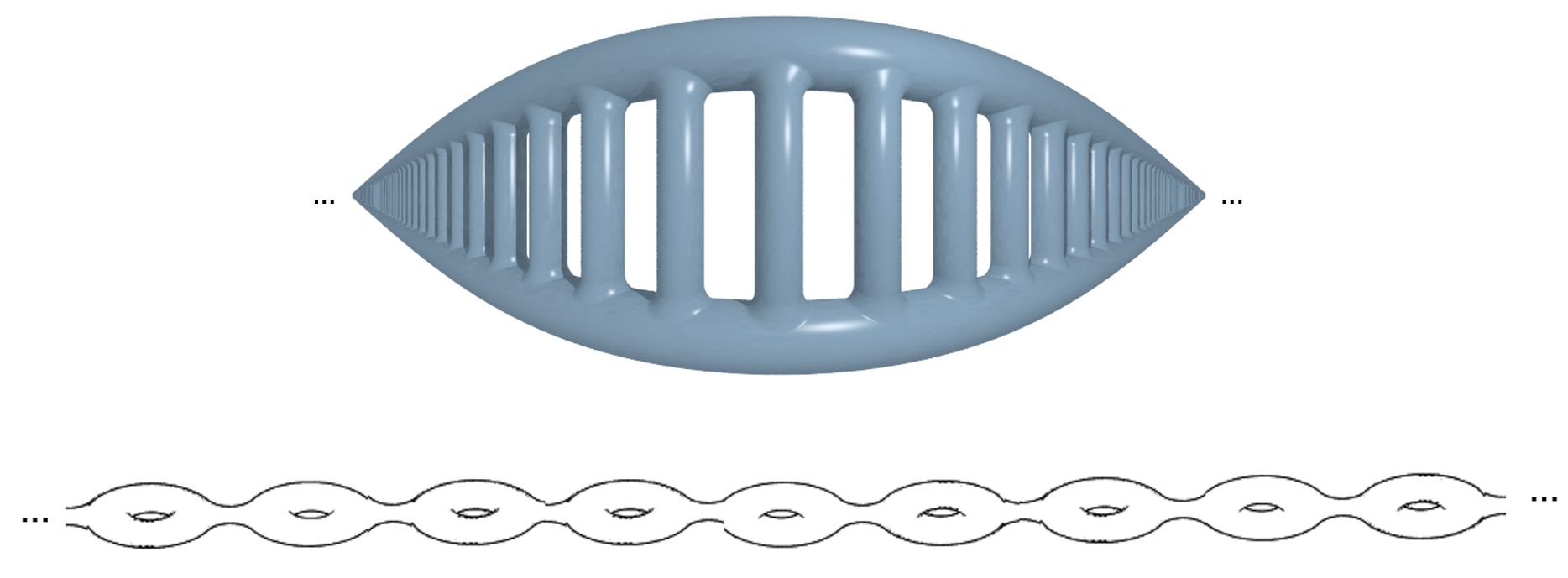
Es una superficie no compacta (orientable, no contiene planos proyectivos) de género infinito y con un único final. La nombraron de esta manera los matemáticos Antony Phillips y Denis Sullivan en un artículo sobre teoría de foliaciones publicado en 1981.
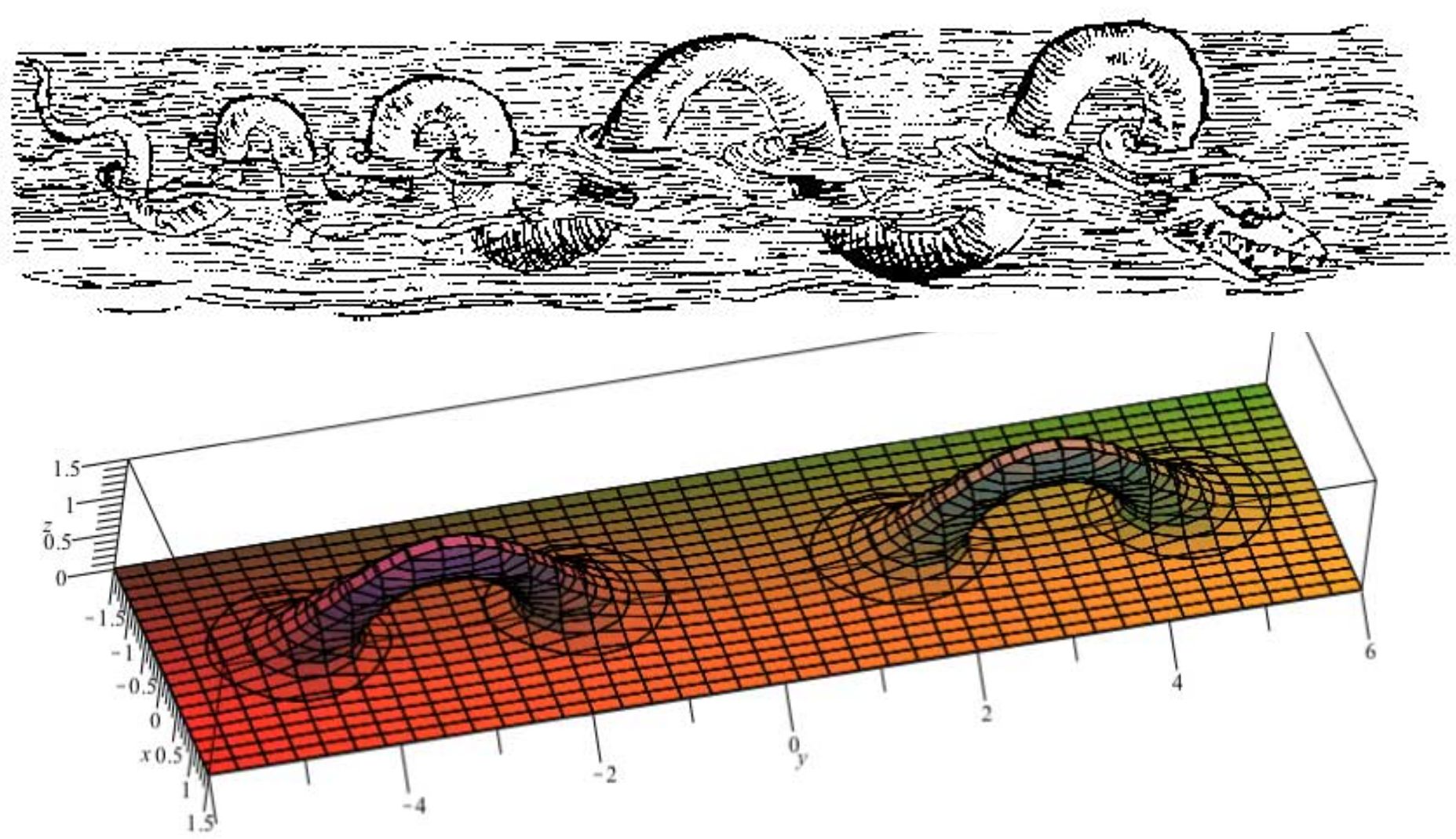
Esta superficie se puede construir a partir de un plano (que puede pensarse como la superficie del lago Ness) al que se le añaden una cantidad infinita de asas (que pueden pensarse como los trozos de cuerpo visibles del monstruo del Lago Ness). Cada asa se añade eliminando dos discos abiertos del plano y “pegando” un cilindro en los huecos originados como se observa en la imagen de debajo. El género de esta superficie es infinito porque hay infinitas asas; solo posee un final porque el plano posee un único final.
La escalera de Jacob
Es una superficie (orientable) de género infinito y con dos finales. La nombró de esta manera el matemático Étienne Ghys en un artículo sobre teoría de foliaciones publicado en 1995.
La superficie se puede describir como la frontera exterior de una escalera infinitamente larga en ambas direcciones. Correspondería a hacer sumas conexas de toros, a partir de uno inicial, en ambas direcciones y de manera indefinida.
El árbol de Cantor
Es una superficie homeomorfa (topológicamente equivalente) a una esfera a la que se le ha eliminado un conjunto de Cantor. Es decir, tiene género cero (no contiene ni toros ni planos proyectivos) e infinitos finales (los infinitos puntos del conjunto de Cantor).
Nota
Se puede probar que cualquier superficie no compacta es homeomorfa a una esfera a la que se le ha quitado un conjunto compacto (que define el conjunto de finales) y se “han pegado” una cantidad finita o infinita de toros y planos proyectivos (que definen el género y la clase de orientabilidad).
Pero esa es otra historia, para la que se necesitan unas cuantas matemáticas más sofisticadas.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia