En 1963, René Sousselier planteó un reto, que intituló “Le Cercle Des Irascibles” (“El círculo de los irascibles”), en la Revue Française de Recherche Opérationelle.

El problema se planteaba en los siguientes términos:

El presidente de un club pensó que sería conveniente organizar una cena de confraternidad entre todos sus miembros. Para no destacar a ningún miembro frente a otro, pensó que deberían sentarse en una mesa redonda. Inmediatamente se tropezó con algunos problemas: en realidad, el club no era una sociedad demasiado amigable. De hecho, cada uno de los socios tenía únicamente unos pocos amigos en el club y aborrecía a todos los demás. Ante este inconveniente, el presidente pensó que debía asegurarse de que cada miembro tuviera a un amigo sentado a cada lado durante la cena. Lamentablemente, no consiguió encontrar por sí mismo una manera de distribuir a los socios del club.

Desesperado, decidió pedir ayuda a un amigo matemático que, poco tiempo después de conocer el problema, respondió de la siguiente manera al presidente del club: «Es absolutamente imposible conseguirlo. Sin embargo, si puedes persuadir a un miembro del club para que no acuda a la cena, entonces todos podrían sentarse junto a un amigo«. El presidente, esperanzado, preguntó al matemático: «¿A qué miembro debo pedirle que se quede fuera?«. El matemático respondió: «Es indiferente. Cualquier socio vale. Por cierto, si tuvieras menos miembros en el club, no te enfrentarías a esta extraña combinación de propiedades«.

Haciendo caso a su amigo, el presidente puso un pretexto cualquiera, se excusó con el resto de los socios del club, y pudo colocar satisfactoriamente a cada miembro con sendos amigos a su izquierda y derecha en la mesa de la cena.

Tras este extenso enunciado preliminar, Sousselier preguntaba:

¿Cuántos miembros tiene del club? ¿A quién le gusta quién y a quién no le gusta quién?

Un año más tarde, T. Gaudin, J. Herz y P. Rossi propusieron una solución en la misma revista utilizando teoría de grafos.

Algunas definiciones previas

Recordemos que, en matemáticas, un grafo G es un conjunto de objetos, los vértices, algunos de los cuales están unidos por aristas, que representan relaciones binarias entre los vértices.

Un camino (sucesión de aristas adyacentes) en un grafo G se llama hamiltoniano si pasa por todos los vértices exactamente una vez. Si el camino es cerrado (el primer y el último vértice alcanzado es el mismo), se habla de un ciclo hamiltoniano; G se llama hamiltoniano si contiene un ciclo hamiltoniano.

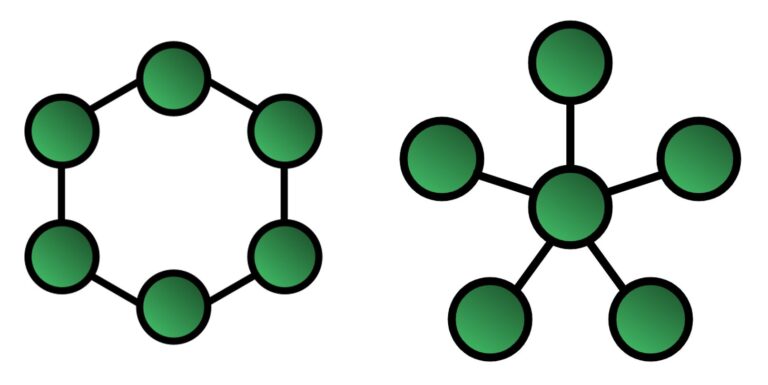
Un grafo G se llama hipohamiltoniano si no es hamiltoniano, pero cualquier grafo construido al eliminar un único vértice (arbitrario) de G es hamiltoniano. Por supuesto, al eliminar este vértice, se suprimen también las aristas que lo alcanzan.

Manera de abordar el problema de Sousselier

Se construye un grafo G con las siguientes reglas: se identifica cada miembro del club con un vértice del grafo en el que dos vértices están unidos si y sólo si los socios que representan son amigos.

El grafo G no puede ser hamiltoniano; si lo fuera, sería posible sentar a todos los miembros del club sin conflictos en una mesa redonda. Pero, según el enunciado, G es hipohamiltoniano.

Así, para resolver el problema, es preciso encontrar el menor (con menos vértices) grafo hipohamiltoniano.

Se puede demostrar que ese grafo es el llamado grafo de Petersen, un grafo con 10 vértices y 15 aristas.

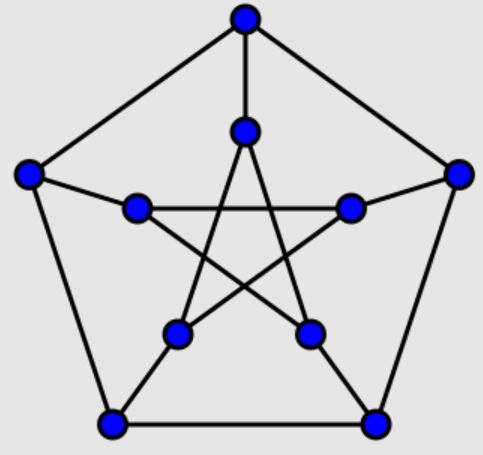
Este grafo no es hamiltoniano, aunque tiene un camino hamiltoniano (que no es un ciclo hamiltoniano).

Grafos hipohamiltonianos

René Sousselier fue el primero en estudiar los grafos hipohamiltonianos. Este problema que propuso en 1963 no es sencillo de resolver; requiere de una maquinaria matemática elaborada. Como otros problemas de enunciado fácilmente comprensible (como el teorema de los cuatro colores), su solución ha necesitado del avance de la teoría matemática de grafos.

El informático teórico Václav Chvátal demostró en 1973 que para todo n suficientemente grande existe un grafo hipohamiltoniano con n vértices. Posteriormente se demostró que tales grafos existen para todo n mayor o igual a 18.

En este momento, se conoce la lista completa de grafos hipohamiltonianos con 17 o menos vértices: el grafo de Petersen (10 vértices), un grafo de 13 vértices y un grafo de 15 vértices (encontrados mediante búsquedas con ordenador de Herz, 1968), y cuatro grafos de 16 vértices (uno de ellos denominado grafo de Sousselier).

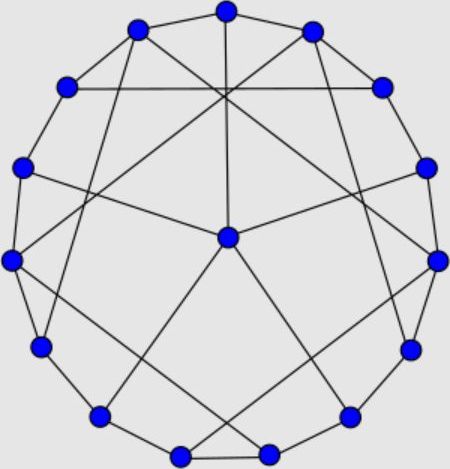
Se sabe que existen 14 grafos hipohamiltonianos de 18 vértices y 34 de 19 vértices. Además, el número de grafos hipohamiltonianos crece como una función exponencial del número de vértices; pero queda mucho por encontrar…

Referencias

• T. Gaudin, J. Herz et P. Rossi, Solution du probleme no.29, Rev. Franc. Rech. Operat., vol. 8, 1964, 214–218
• R. Sousselier, Probleme no. 29: Le cercle des irascibles, Rev. Franc. Rech. Operat., vol. 7, 1963, 405–406
• D. A. Holton and J. Sheehan, The Petersen Graph, Cambridge University Press, 1993, Págs. 214-248
• Sousselier’s Problem, Futility Closet, 28 agosto 2024
• Hypohamiltonian graph, Wolfram MathWorld
• Number of hypohamiltonian graphs on n vértices (A141150), OEIS

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia