Los fractales son unos curiosos objetos matemáticos que gozan de una cierta popularidad fuera de la comunidad matemática, y científica, desde que el matemático polaco, nacionalizado francés y estadounidense, Benoît Mandelbrot (1924-2010), considerado el padre de la geometría fractal, realizara una importante labor divulgativa sobre ellos, primero con el artículo ¿Qué longitud tiene la costa de Gran Bretaña? (Revista Science, 1967) y posteriormente con los libros Los objetos fractales: forma, azar y dimensión (1975) o La geometría fractal de la naturaleza (1982), entre muchos otros.

En la entrada del Cuaderno de Cultura Científica titulada Sucesiones fractales hablábamos de un tipo de sucesiones de números enteros que compartían con los objetos fractales una de sus propiedades definitorias, la autosemejanza (para una explicación divulgativa de las mismas puede leerse la entrada Fractus, arte y matemáticas). Más aún, en una entrada posterior, titulada Sucesiones fractales: del número a la nota musical, explicábamos como el compositor minimalista estadounidense Tom Johnson (1939) las había utilizado en algunas de sus composiciones musicales, por ejemplo, La melodía racional XV y la pieza La vie est si court, las cuales fueron explicadas en dicha entrada.

La “sucesión del infinito” que, en particular, es una sucesión fractal y de la que vamos a escribir en esta entrada, fue descubierta por el músico danés Per Nørgård, que la utilizó como base matemática de muchas de sus composiciones musicales.

Per Nørgård, descubridor de la sucesión del infinito

El compositor, teórico de la música y profesor danés Per Nørgård (1932) es una figura fundamental en la música danesa contemporánea. Ha escrito alrededor de 400 composiciones, que incluyen seis operas, ocho sinfonías, tres ballets, música para orquesta, conciertos, obras corales y vocales, música de cámara, piezas para instrumentos solistas y también bandas sonoras para películas. Entre sus composiciones más importantes se podrían citar Voyage into the Golden Screen / Viaje a la pantalla dorada (1968), para orquesta, la Sinfonía no. 2 (1970), para orquesta, la ópera Gilgamesh (1972), premiada con el Nordic Music Prize en 1974, la Sinfonía no. 3 (1972), para dos coros y orquesta, la ópera Siddharta (1979), la pieza para un solo instrumento de percusión I Ching (1982) o la ópera Det Guddommelige Tivoli / El circo divino (1982). Además, ha recibido muchos reconocimientos a lo largo de su extensa carrera, como el Premio (internacional) Ernst von Siemens, conocido como el Premio Nobel de la Música, en 2016, o el Premio (internacional) Wihuri Sibelius, en 2006, por mencionar algunos.

Si consultamos la biografía de Per Nørgård que aparece en la base de datos sobre compositores del Institut de Recherche et Coordination Acoustique/Musique (IRCAM), un instituto francés de investigación sobre música y acústica, asociado al Centro Nacional de Arte y Cultura Georges Pompidou de París (cuya dirección web es brahms.ircam.fr), se mencionan las siguientes cuestiones respecto a su música. “Tras experimentar con collages musicales a finales de la década de 1950, Per Nørgård centró su atención en la música serial en los primeros años de la nueva década, desarrollando su propia técnica conocida como sucesión del infinito”, que es una de las herramientas musicales más importantes del conjunto de su producción musical. Además, no podemos olvidar que esta sucesión del infinito es un objeto matemático, una sucesión de números enteros con una serie de propiedades que la hacían interesante para las composiciones musicales que Per Nørgård quería componer y que utilizó en obras como Viaje a la pantalla dorada (1968), la Sinfonía no. 2 (1970), la Sinfonía no. 3 (1972) o I Ching (1982). Además de la sucesión del infinito, también utilizó el número de oro y la sucesión de Fibonacci, aunque en menor medida.

Por otra parte, “en 1979, durante una exposición en el Museo de Arte Moderno de Luisiana (Dinamarca), el compositor descubrió la obra del pintor suizo, uno de los primeros artistas asociados con el Art Brut (arte marginal), Adolf Wölfli. La interpretación de los criptogramas del artista esquizofrénico atrajo la práctica compositiva de Nørgård hacia el expresionismo. El resultado es un juego de intensidades, cambios bruscos de humor y modificaciones violentas del sonido y, además, un desbordamiento del flujo musical. Esta aparición del conflicto y la irracionalidad en su obra es una respuesta directa a la última década de composiciones matemáticamente regulares”. Entre las obras que pertenecen a este periodo están la Sinfonía no. 4 (1981) y la ópera sobre la vida de Wölfli, El circo divino (1982).

La sucesión del infinito

El compositor Per Nørgård descubrió (utilizamos este término y no “inventó”, ya que es el que utilizaba el propio Nørgård) la sucesión de números enteros que bautizó con el nombre de Uendelighedsrækken (en danés), que he traducido para esta entrada como sucesión del infinito, en 1959, años antes de que los fractales se hicieran conocidos a través de la labor divulgativa del matemático Benoit Mandelbrot, y que utilizó en muchas de sus composiciones, especialmente de las décadas de 1960 y 1970. La primera obra en la que utiliza la sucesión del infinito es su obra Viaje a la pantalla dorada (1968), en la cual utiliza 1.024 elementos de la sucesión en su versión musical. La siguiente obra en la que la utilizaría es la Sinfonía no. 2 (1970), con una utilización más compleja con 4.096 elementos de la sucesión.

Si consultamos la partitura de la obra Viaje a la pantalla dorada podemos ver una versión musical de la sucesión del infinito, cuyas primeras 64 notas (interpretadas en esta obra por las dos flautas) aparecen en la siguiente imagen.

A partir de la anterior imagen, extraída de la partitura de la obra Viaje a la pantalla dorada, vamos a escribir la sucesión de números enteros, que Nørgård descubrió, realizando el proceso inverso al que realizó el compositor al pasar de la sucesión de números a la sucesión de notas musicales. Para ello empezamos indicando que el punto inicial es la primera nota de la sucesión musical, que en este caso es “Sol” y que se corresponde con el número 0. A partir de ahí los números enteros de la sucesión van a indicar, para cada nota, la cantidad de semi-tonos que esa nota está por encima (positivo) de “Sol”, luego es más aguda, o por debajo (negativo), luego es más grave. Así, el segundo número es un 1 puesto que la siguiente nota es “La bemol” que es un semi-tono más alta (aguda) que “Sol” (de “Sol” a “La” subimos un tono, pero el bemol indica que baja un semi-tono, luego de “Sol” a “La bemol” sube un semi-tono). Como la tercera nota es “Fa sostenido”, que es un semi-tono más baja (grave) que “Sol” (de “Sol” a “Fa” se baja un tono, pero el sostenido indica que la nota sube un semi-tono, entonces el “Fa sostenido” es un semi-tono más bajo que “Sol”), el siguiente número de la sucesión es -1. El cuarto número es 2, ya que la cuarta nota es un “La”, un tono, luego dos semi-tonos, por encima de “Sol”. De esta manera descubrimos que los 64 primeros números de la sucesión del infinito, en correspondencia con las notas musicales de la partitura, son los siguientes.

De hecho, los 86 primeros términos de la sucesión del infinito, que es la sucesión A004718 de la Enciclopedia online de sucesiones de números enteros, son los siguientes.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

Existen varias formas de generar esta sucesión de números enteros. La más simple es mediante una fórmula recursiva.

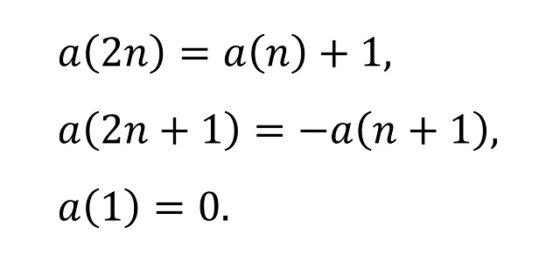
En la propia fórmula recursiva ya podemos percibir las propiedades relacionadas con la autosemejanza, de hecho, la sucesión del infinito es una sucesión fractal, que buscaba el compositor y que veremos más adelante.

Un proceso iterativo infinito

Otro método de construcción de esta sucesión es un proceso iterativo infinito proyectando un “segmento” inicial de dos números, o dos notas. El segmento inicial es 0 y 1 (“Sol” y “La bemol”) y la variación entre los dos (segundo menos primero) es + 1, entonces vamos a proyectar los dos primeros términos de la sucesión utilizando esa variación de la siguiente forma. Al segundo término le aplicamos la variación 1 + 1 y se convierte en el cuarto término 2, mientras que al primer término le aplicamos el opuesto 0 – 1 y se convierte en el tercer término – 1, como se muestra en la siguiente imagen. Por lo tanto, tenemos los cuatro primeros términos de la sucesión 0, 1, -1, 2.

A continuación, avanzamos una posición y el segmento que nos va a determinar las dos siguientes notas es el segmento 1 y -1, y la variación entre los dos es -2. Ahora aplicaremos esta variación a los dos últimos términos de la sucesión que vamos construyendo, – 1 y 2. Al segundo de esos dos términos le aplicamos la variación 2 – 2 y se convierte en el sexto término de la sucesión 0, mientras que al primero le aplicamos el opuesto -1 + 2 = 1 y se convierte en el quinto término de la sucesión, como se muestra en la siguiente imagen. De esta forma quedan determinados los seis primeros términos de la sucesión 0, 1, -1, 2, 1, 0

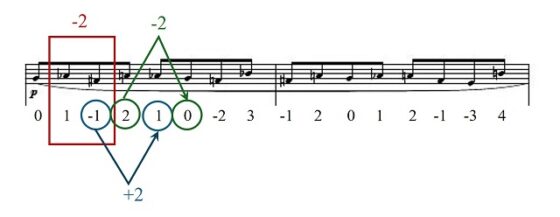
Volvemos a avanzar una posición y el segmento que nos va a determinar ahora las dos siguientes notas es el segmento -1 y 2, por lo que la variación es +3. Aplicando, como en los casos anteriores, esta variación a los dos últimos términos construidos 1 y 0, se obtienen los dos siguientes, séptimo y octavo, -2 y 3, como se puede ver en la siguiente imagen.

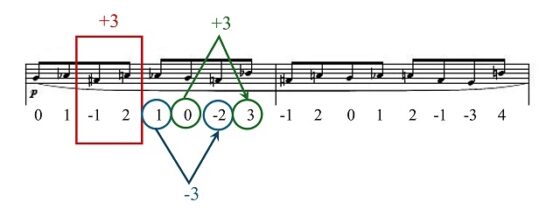
Y así se continuaría, podéis observar el siguiente paso en la siguiente imagen, en un proceso iterativo infinito que nos genera la sucesión del infinito.

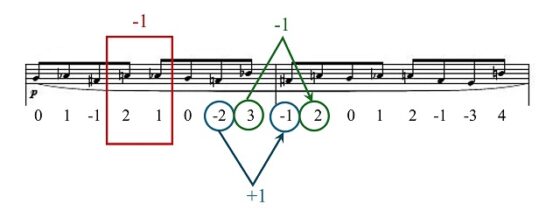
Existe otro proceso iterativo infinito para generar la sucesión del infinito denominado “desplegado”, pero que no vamos a explicar en esta entrada.

Construcción con números binarios

En la entrada Sucesiones fractales mostrábamos un ejemplo de una sucesión fractal construida a partir de la representación binaria de los números naturales (sobre la representación binaria puede leerse la mencionada entrada Sucesiones fractales, o con una explicación más extensa y detallada la entrada Las bases de numeración o cómo hacer trucos de magia binarios), incluido el 0, en concreto, la sucesión consistía en la cantidad de unos (1s) de la expresión binaria de los números enteros no negativos. Así mismo, en la entrada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez se mostraba un proceso de construcción de la conocida sucesión fractal de Thue-Morse a través de las representaciones binarias de los números, en concreto, sumando los unos (1s) de la representación binaria de los números, empezando en 0, si es una cantidad par se considera el número 0 y si es impar el número 1.

También existe un método de construcción de la sucesión del infinito mediante la representación binaria de los números naturales, empezando en cero. Por lo tanto, empecemos considerando la representación binaria de los números, que mostramos en la siguiente imagen entre el 0 y el 38.

Expliquemos, a continuación, cómo se construye la sucesión del infinito a partir de esas representaciones binarias. Para obtener los términos de la sucesión del infinito se realiza la “suma” de los unos (1s), pero teniendo en cuenta “cambios de signo” cuando aparecen ceros (0s) en la representación binaria, leyendo estas de izquierda a derecha. Así, para la representación 1111 (del número 15) se obtiene el término 4 (suma de los cuatro 1s); para la representación 1110 (del número 14) se obtiene -3 (suma de tres 1s, más un 0 que cambia el signo); para la representación 1101 (del número 13) se obtiene -1 (suma de dos 1s, luego 2, con el 0 se cambia el signo a -2 y luego se suma el último 1, luego -2 + 1 = -1); para 1010 (número 10), se obtiene 0 (se empieza sumando 1, que cambia de signo con el 0, a -1, se suma 1, luego 0, y el cambio de signo, del último 0, no modifica nada); o para 1001 (número 9), se obtiene 2 (primero 1, que cambia de signo con el primer 0, luego -1, que vuelve a cambiar de signo con el segundo 0, luego 1, al que se le suma el último 1, finalmente 2). Veamos ahora la tabla de dicha construcción.

Sucesiones fractales

Vamos a terminar esta entrada viendo las propiedades que hicieron que la sucesión del infinito fuera importante como herramienta de creación musical para el compositor Per Nørgård, propiedades de autosemejanza. Aunque antes recordemos la definición de sucesión fractal o autosemejante.

Una sucesión (infinita) de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.

Veamos un ejemplo. Consideremos la sucesión finita de números 1, 2, 2, 3, 2, 3, 3 y construyamos la sucesión infinita que consiste en repetir la secuencia anterior de forma infinita, es decir, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … Ahora si eliminamos de la sucesión infinita todos los números que están en posiciones pares, los que nos quedan, que son los que están en las posiciones impares, siguen siendo la sucesión original, como queda de manifiesto en la siguiente imagen.

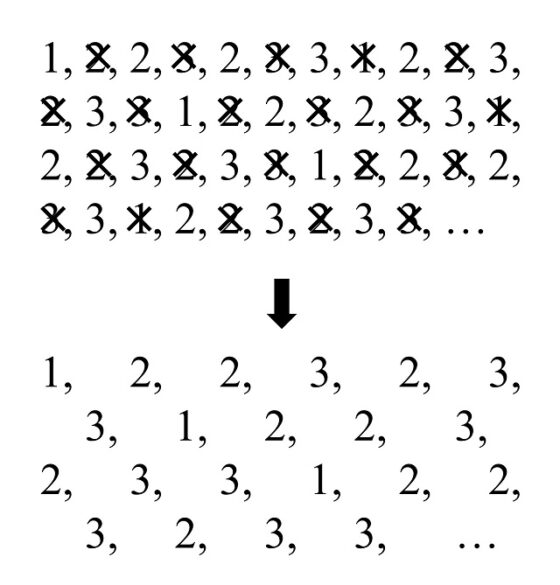
La sucesión del infinito es autosemejante

Volvamos a la sucesión inventada, o descubierta, por el compositor danés Per Nørgård. Empecemos recordando los primeros términos de la sucesión, que ya mostramos antes.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

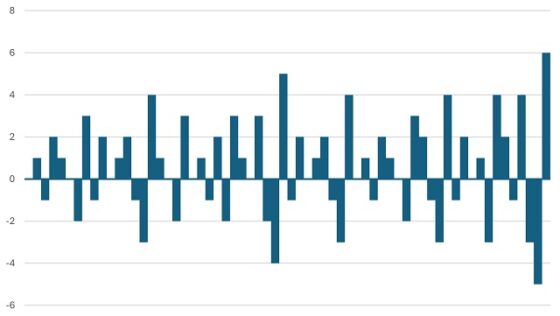
Ahora, vamos a eliminar los términos que están en posiciones pares, quedarnos con los que están en posiciones impares y veamos qué ocurre.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

Si nos fijamos bien en el resultado, lo que nos ha quedado es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero invertida, es decir, con el signo opuesto (0, -1, 1, -2, -1, 0, 2, -3, …). Por lo tanto, la sucesión del infinito tiene una cierta propiedad de autosemejanza, pero con inversión del signo. Esta propiedad está reflejada en la fórmula recursiva, a(2n + 1) = – a(n + 1).

Por otra parte, si eliminamos los términos que están en posiciones impares y nos quedamos con los términos de las posiciones pares, ocurre lo siguiente.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

De nuevo, si nos fijamos en el resultado, lo que queda es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero desplazada en una unidad, es decir, se suma 1 a cada término de la sucesión del infinito (1, 2, 0, 3, 2, 1, -1, 4, …). Otra propiedad del tipo de autosemejanza, pero con traslación de una unidad. También esta propiedad está reflejada en la fórmula recursiva, a(2n) = a(n) + 1.

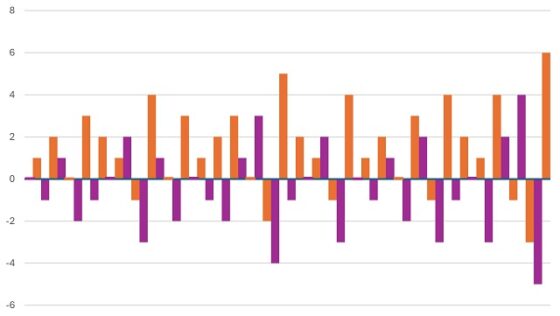
Podemos cuestionarnos si la sucesión del infinito es una sucesión fractal en sentido estricto y la respuesta es, claramente, afirmativa. De hecho, es lo que se llama una sucesión fractal de razón d = 4, es decir, el subconjunto de la sucesión que no eliminamos son el primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, los números que están en las posiciones que son múltiplos de d más 1 y de esta forma obtenemos de nuevo la sucesión original. Veamos si es así para la sucesión del infinito.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

La propiedad de ser una sucesión fractal de razón 4 también se podía observar en la fórmula recursiva, ya que a(4n + 1) = – a(2n + 1) = a(n + 1).

La sucesión del infinito es una sucesión con muchas más propiedades matemáticas, pero en las que no vamos a entrar ahora. Simplemente terminaremos esta entrada viendo la relación que tiene con la sucesión de Thue-Morse.

La sucesión de Thue-Morse

En la entrada del Cuaderno de Cultura Científica titulada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez [https://culturacientifica.com/2023/04/05/la-sucesion-fractal-de-thue-morse-y-la-partida-infinita-de-ajedrez/] presentamos la sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas, desde la combinatoria de palabras a problemas de ajedrez, pasando por la geometría diferencial, la teoría de números, el análisis matemático de funciones, la física matemática, los cuasi-cristales o la teoría de grupos.

Los primeros términos de la sucesión de Thue-Morse (que es la sucesión A010060 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son los siguientes.

0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …

Resulta que si consideramos la sucesión del infinito módulo 2, es decir, los números pares serán 0 y los números impares 1, entonces se obtiene la sucesión de Thue-Morse. A continuación, volvemos a mostrar los primeros términos de la sucesión del infinito, para que podáis comprobar que los números pares coinciden con los 0s de la sucesión de Thue-Morse y los impares con los 1s.

0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …

Bibliografía

1.- Benoît Mandelbrot, Los objetos fractales: forma, azar y dimensión, colección Metatemas, Tusquets, 1984.

2.- Benoît Mandelbrot, La geometría fractal de la naturaleza, colección Metatemas, Tusquets, 1982.

3.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.

4.- Tom Johnson, Self-similar Melodies, Editions 75, 2014.

5.- Tom Johnson, Rational Melodies, Editions 75, 1982.

6.- Página web del compositor Per Nørgård [http://www.pernoergaard.dk/] (enlace roto)

7.- Jørgen Mortensen, Uendelighedsrækken / La serie del infinito

8.- Yu Hin (Gary) Au, Christopher Drexler-Lemire, Jeffrey Shallit, Notes and note pairs in Nørgård’s infinity series, Journal of Mathematics and Music, vol. 11, no. 1, pp. 1-19, 2017.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica