Hace unas semanas hablamos en el Cuaderno de Cultura Científica de las llamadas sucesiones fractales, o sucesiones autosemejantes, en la entrada titulada Sucesiones fractales], que continuamos con la entrada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez, en la que mostrábamos una sucesión autosemejante concreta, conocida con el nombre de sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas. El objetivo de la presente entrada es mostrar algunos ejemplos de cómo el compositor minimalista estadounidense Tom Johnson utiliza estas sucesiones para componer algunas de sus composiciones musicales.

Empecemos recordando qué son las sucesiones fractales o autosemejantes. Una sucesión (infinita) de números enteros se dice que es una sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan siguen siendo toda la sucesión.

Pongamos un ejemplo de sucesión autosemejante, en particular, aprovechemos para mostrar un nuevo ejemplo, no comentado en las entradas anteriores. Se trata de la sucesión de la cantidad de maneras que existen de expresar los cuadrados de los números enteros positivos, 0, 1, 2, 3, 4, 5, 6, …, como suma de dos cuadrados (sin importar el orden), a cuyos miembros vamos a denotar por a(n). Para calcular los primeros términos de esta sucesión nos viene muy bien tener en cuenta la sucesión de los números cuadrados (0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, …) y ver cómo expresar el cuadrado de cada número entero no positivo como suma de dos de los cuadrados de esa lista.

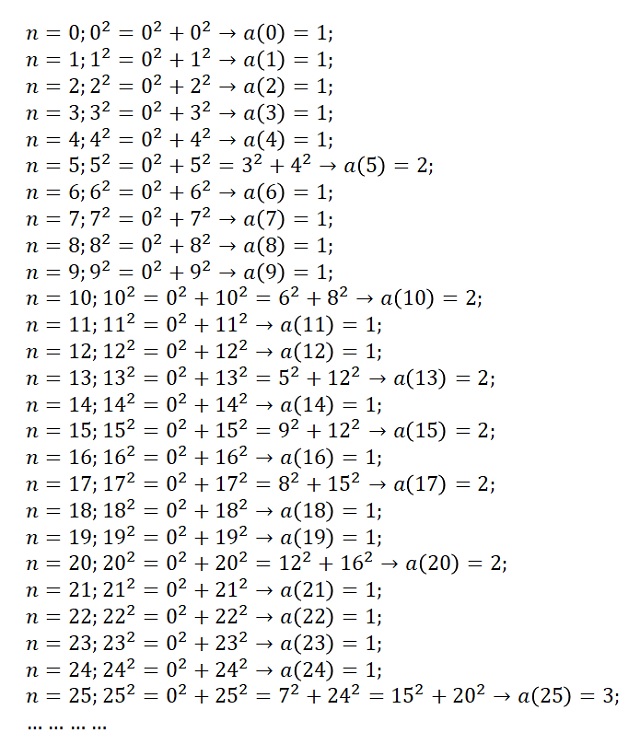
En la imagen anterior hemos obtenido los miembros de la sucesión hasta a(25), que son: 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 3. Esta sucesión infinita, que es la sucesión A063014 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, cuyos primeros términos son

1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 3, 2, 1, 1, 2, 2, 1, 1, 1, 2, 2, 1, 2, 1, 2, 2, 2, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 1, 5, 1, 1, 2, 1, 2, 1, 1, 2, 2, 3, 1, 1, 2, 1, 2, 1, 2, 1, 1, 5, 1, 2, 1, 2, 2, 2, 1, 1, 1, 2, 1, 2, 1, 1, 3, 2, 2, …

es una sucesión autosemejante. De hecho, es una sucesión fractal de razón 2, como se muestra en la siguiente imagen. Recordemos que una sucesión infinita se dice que es una sucesión fractal de razón d si nos quedamos con un primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, eliminamos el resto, y seguimos obteniendo la sucesión infinita inicial.

Luego, efectivamente es una sucesión autosemejante de razón 2. Pero, curiosamente, también es una sucesión autosemejante de razón 3, como vemos en la siguiente imagen.

El compositor minimalista Tom Johnson

Empecemos presentando al compositor del que vamos a hablar en esta entrada, Tom Johnson, del que ya hemos hablado en algunas otras entradas, como Las vacas de Narayana, la versión hindú de los conejos de Fibonacci o Teselaciones rítmicas perfectas.

Tom Johnson (Greeley, Colorado, EE.UU., 1939), es un compositor minimalista y teórico de la música estadounidense. Se graduó en la Universidad de Yale, donde obtuvo además su grado avanzado en música. Viajó a Nueva York en 1967 y fue alumno del compositor Morton Feldman (1926-1987), uno de los artífices, junto con John Cage (1912-1992), de la música aleatoria. Entre 1971 y 1983 fue crítico de música en The Village Voice, el primer periódico semanal alternativo (EEUU) de noticias y cultural. En 1983 se trasladó a París, donde vive con su mujer, la artista donostiarra Esther Ferrer.

Es un compositor minimalista, ya que trabaja con formas simples, escalas limitadas y de manera general, con material reducido. Y dentro del minimalismo destaca por el uso de las matemáticas en su proceso creativo. Sucesiones de números (Fibonacci, Narayana, autosemejantes, …), autómatas, números (contar), números binarios, números primos (Mersenne), geometría, trigonometría, simetrías, teselaciones, curvas fractales, grafos, combinatoria (permutaciones, combinaciones, cuadrados latinos, cuadrados mágicos, el problema de las colegialas de Kirkman, teoría de bloques, …), el triángulo de Pascal, cuadrados mágicos geométricos, son algunas de las teorías matemáticas que utiliza en sus composiciones.

Tom Johnson ha escrito de su música: “quiero encontrar la música, no componerla”, o como decía su maestro Morton Feldman “Deja a la música hacer lo que quiere hacer”. Mientras John Cage, o Morton Feldman, realizan esta búsqueda mediante el azar, Tom Johnson lo hace mediante las matemáticas.

En su artículo Found Mathematical Objects / Objetos matemáticos encontrados (2001) Tom Johnson explica su filosofía artística y empieza así:

La idea es sencilla. Encuentra un objeto, cualquier objeto, decláralo obra de arte, y es una obra de arte. El arte se convierte en algo verdaderamente objetivo, sólo un objeto, las técnicas artísticas se vuelven innecesarias y, al mismo tiempo, se siembran las semillas del arte «no intencional». Este principio de Marcel Duchamp, el «readymade» o el «objet trouvé», se reconoce ahora en todas partes como una forma perfectamente válida de hacer arte. Una generación de artistas Fluxus desarrolló este punto de vista, John Cage lo adaptó para componer música mediante operaciones fortuitas, y ahora es bastante natural que un compositor o artista pueda elegir trabajar con un objeto matemático encontrado, como el triángulo de Pascal o la serie Narayana o algún autómata, lo mismo que con un urinario, una rueda de bicicleta, un peine o un botellero.

Entre sus obras encontramos óperas como Riemannoper (1988), Trigonometría (1997) o la más famosa La ópera de las cuatro notas (1972), que fue representada en España en 2015 por Vania Produccions bajo la dirección de Paco Mir (que muchos conoceréis por ser uno de los miembros del trío Tricicle) o composiciones musicales muy creativas e interesantes, como Una hora para piano (1972), Nueve campanas (1979), Simetrías (1981), Dúos para contar (1982), Melodías racionales (1982), Melodías infinitas (1982), Música para 88 (1988), Las vacas de Narayana (1989), Kentzy Loops (2000), Galileo (2001), Mosaicos (2002), Combinations for String Quartet (2003) o Ritmos de Vermont (2008).

Ha escrito libros como la colección de artículos de crítica musical The voice of the new music (Apollohuis, 1989), Self-similar Melodies (Editions 75, 1996), Looking at numbers (Birkhauser, 2014) o Finding Music. Writings 1961-2018 (MusikTexte, 2019).

La melodía racional XV

El compositor Tom Johnson utiliza las sucesiones autosemejantes de formas diferentes para componer sus obras musicales. En esta entrada vamos a mostrar dos ejemplos, La melodía racional XV y la pieza La vie est si court.

La melodía racional XV está compuesta a partir de una sucesión autosemejante de razón 2. Esta composición pertenece a un grupo de veintiuna melodías racionales que el compositor minimalista Tom Johnson compuso en 1982 bajo el título Rational Melodies / Melodías Racionales.

De forma paralela a como suelo sugerir, cuando hablamos de juegos matemáticos, que lo primero es jugar, ahora recomiendo escuchar algunas de las melodías racionales (por ejemplo, las melodías racionales I, II, X y XIII, para empezar) y, en particular, la melodía racional XV, de la que vamos a hablar. Puedes escucharlas en diferentes plataformas (YouTube, Spotify, etc), en particular, en el canal de YouTube de Eberhard Blum o de Dedalus, que hacen dos interpretaciones diferentes de las melodías racionales.

Aquí os dejo la versión, para flauta, de Eberhard Blum de la melodía racional XV:

Y aquí os dejo la versión, para cello y violín, de Dedalus de la melodía racional XV:

En la introducción de la publicación de las partituras de las Melodías Racionales, que recordemos que publica en 1983, su autor escribe lo siguiente:

La racionalidad o, más precisamente, la lógica deductiva se ha usado rara vez como factor de control en la composición musical. Normalmente los compositores están más interesados en inspiración, intuición, sentimientos y expresión interna. Últimamente, sin embargo, ha aparecido una tendencia por parte de los compositores a renunciar al control individual sobre cada nota confiando en factores externos. Existen, por ejemplo, piezas controladas por el viento, por el azar, por la idiosincrasia de los magnetófonos o por variaciones impredecibles en un circuito eléctrico, y creo que componer adhiriéndose rigurosamente a premisas lógicas implica un proceso similar de pensamiento.

La autosemejanza ha sido un concepto central en la obra de Tom Johnson. Empezó a trabajar con sucesiones autosemejantes entre 1979 y 1980. Tres fueron las influencias que le llevaron hacia este tema. Por una parte, el matemático polaco, nacionalizado francés y estadounidense, Benoit Mandelbrot (1924-2010) publicó su libro Fractals: Form, Chance and Dimension en 1977 que fue leído con mucho interés por Tom Johnson. La segunda fue la lectura, años después de su publicación, del artículo sobre la “curva dragón” publicado por el divulgador estadounidense Martin Gardner (1914-2010) en su columna de Juegos Matemáticos de la revista Scientific American, en 1967. Y finalmente, su encuentro con el matemático y músico David Feldman, en 1979, con quien realizó un pequeño estudio de “melodías que se presentan a si mismas en dos (o más) tempi a la vez”, es decir, melodías autosemejantes.

La melodía racional XV, junto al resto de las melodías racionales, fueron publicadas en 1983, pero realmente las compuso dos y tres años antes de su publicación.

Empecemos por la sucesión autosemejante que utiliza Tom Johnson en esta pieza. Si miramos a la primera línea de la partitura (véase la siguiente imagen) veremos el “germen” de la sucesión infinita fractal de razón 2.

Si denotamos por números las diferentes notas obtenemos la sucesión finita

1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5,

donde cada número natural se corresponde con una nota musical cada vez más grave (1 = La, 2 = Sol, 3 = Fa, 4 = Mi, 5 = Re), es decir, más baja en el pentagrama. Esta sucesión finita es el “germen” de una sucesión infinita autosemejante que se obtiene poniendo infinitas copias de la misma, una a continuación de la otra, como se muestra en la siguiente imagen.

Esta sucesión es autosemejante de razón 2 como se puede observar fácilmente, ya que al eliminar los números que están en las posiciones pares, lo que queda (posiciones impares) sigue siendo la misma sucesión infinita. Es decir, la sucesión infinita está dentro de ella misma.

Si nos fijamos en las dos primeras líneas de la anterior imagen, que son dos copias de la sucesión finita germen [1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5], al eliminar los números que están en las posiciones pares, nos queda una copia de la sucesión germen [1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5], y así ocurre para el resto.

Para entender cómo transforma Tom Johnson esta sucesión fractal en una composición musical debemos de darnos cuenta que podemos ver el anterior proceso desde un punto de vista diferente, añadir números en lugar de quitarlos. De esta forma, partimos de la sucesión infinita y entre cada par de números consecutivos introducimos un número (los que antes quitábamos), de esta forma construimos una sucesión más grande que contiene a la anterior, pero que resulta que es exactamente igual a ella misma. Veámoslo de forma sencilla con una sola copia de nuestra sucesión germen:

[1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5].

Y vamos a incluir entre cada dos números consecutivos los números que antes quitábamos, que si nos fijamos bien primero son los que están en posiciones pares (2, 3, 4, 5, 3, 5, 5) y luego están en posiciones impares (1, 2, 2, 3, 2, 4, 3, 5), quedando (hemos indicado con negrita los números que hemos incluido):

[1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5, 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5],

es decir, dos copias de la sucesión germen, que incluyen a esta en su interior (los números que NO están en negrita). Y es precisamente este proceso que acabamos de ejemplificar el que utiliza Tom Johnson para componer la melodía racional XV.

La primera línea de la partitura mostrada arriba, que es la versión musical de la sucesión germen 1, 2, 2, 3, 2, 4, 3, 5, 2, 3, 4, 5, 3, 5, 5 (1 = La, 2 = Sol, 3 = Fa, 4 = Mi, 5 = Re), es la melodía base de la melodía racional XV, con silencios entre cada dos notas (que pan a ser las posiciones donde se van a incluir las nuevas notas). Entonces en cada nueva línea se va incluyendo una nueva nota (número) intermedio, como se muestra en la siguiente imagen de la partitura (yo he añadido los números, azules en la melodía inicial y rojos los que se corresponden con las notas añadidas), que muestra la mitad del proceso.

Al final del proceso, que se muestra en la siguiente imagen, se concluye con dos copias de la melodía (sucesión germen) de la composición, pero tocadas el doble de rápido, ya que ahora no hay silencios intermedios.

Si ahora volvéis a escuchar la melodía racional XV podréis escuchar el proceso descrito.

La vie est si courte

En 1998 Tom Johnson compuso la obra La vie est si courte / La vida es tan corta, que está compuesta de variaciones sobre un bucle de 20 tiempos que gira continuamente alrededor de los ocho instrumentos, flauta, clarinete, trompeta, trombón, marimba, violín, viola y violonchelo.

En su libro Finding Music, Writings 1961-2018, Tom Johnson escribe de la composición La vie est si courte lo siguiente:

Cuando escribí por primera vez la melodía de esta pieza, parecía música vocal e incluso tenía un texto que la acompañaba.

Después de muchas páginas de esbozos vocales tipo madrigal, me di cuenta de que las cosas polirrítmicas que quería hacer eran en realidad mucho más apropiadas para instrumentos, y que esto sería un buen material para una pieza que me acababan de encargar para Musica Temporale. Sin embargo, decidí conservar parte del texto como título para la pieza instrumental. Las palabras siempre nos ayudan a recordar las melodías y, de hecho, puede ser una buena idea que los músicos canten el tema una vez para el público antes de empezar la composición propiamente dicha.

El texto de la pieza, como se puede ver en la partitura es “La vie est si courte. La mort est si longue” (La vida es tan corta. La muerte es tan larga).

Si miramos al inicio de la partitura (primera línea, en clave de Sol) podremos observar cual es la sucesión finita germen, en la cual se incluyen los silencios, que genera la sucesión infinita fractal, mediante la repetición infinita de la sucesión germen. La sucesión finita germen tiene 20 números (20 tiempos en la partitura, que se pueden ver indicados en la siguiente imagen que el propio Tom Johnson ha incluido en su video de la serie Illustrated Music de YouTube) son, siendo 0 el número que se corresponde con un silencio,

1, 0, 2, 0, 3, 4, 2, 0, 3, 0, 5, 0, 3, 0, 2, 4, 3, 0, 2, 0,

donde 1 = Mi, 2 = Sol, 3 = La, 4 = Si, 5 = Re.

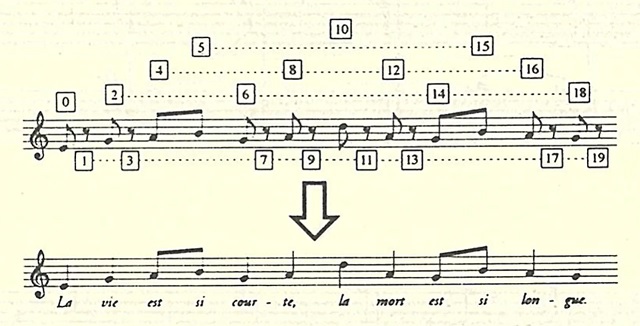
La sucesión numérica infinita que se genera a partir de la sucesión germen de 20 números es efectivamente autosemejante de razón 3, como se observa en la siguiente imagen.

Esta propiedad puede verse en la partitura, ya que el segundo instrumento (segunda línea de la partitura) toca una de cada tres notas de la melodía del primer instrumento (primera línea), pero en clave de Fa, y como la sucesión es autosemejante de razón 3, entonces interpreta la misma melodía, pero tres veces más lenta.

Volviendo a la sucesión infinita, no solo es autosemejante de razón 3, sino que también es autosemejante de razón 7, como se muestra a continuación.

La autosemejanza de razón 3 de la anterior sucesión es el elemento a partir del cual Tom Johnson estructura toda la obra, que es una composición para ocho instrumentos. La explicación al detalle la podéis encontrar en el video de la serie Illustrated Music de su canal de YouTube titulado Illustrated Music #9, La Vie est si courte [https://www.youtube.com/watch?v=F7KBTIXNkc8].

La representación gráfica de Tom Johnson

Vamos a terminar esta entrada del Cuaderno de Cultura Científica mostrando la forma en la que el compositor Tom Johnson representa las sucesiones autosemejantes que se generan a partir de una sucesión finita germen.

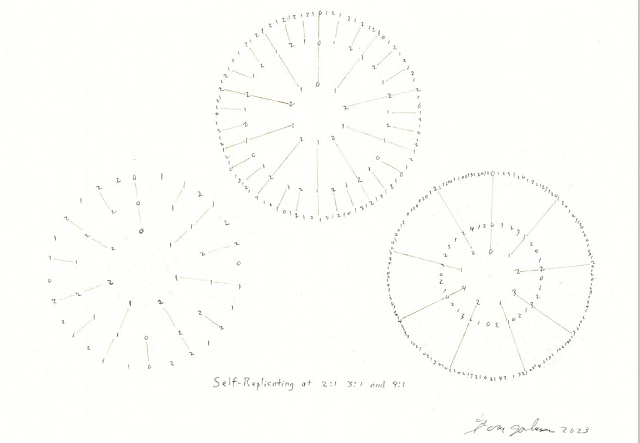
Para empezar, en el centro de la representación dibuja, de forma circular, la sucesión finita germen. Al ser una representación circular es como si repitiéramos la misma sucesión finita de forma infinita generándose así la sucesión infinita. Por ejemplo, la representación de la izquierda en la anterior imagen se corresponde con la sucesión autosemejante de razón 2 que tiene como sucesión germen 0, 1, 1, 2, 1, 2, 2 (esta sucesión ya aparece en su libro Self-Similar Melodies, de 1996, aunque expresada como 1, 2, 2, 3, 2, 3, 3). Si en la circunferencia central se representa la sucesión germen (en este caso, 0, 1, 1, 2, 1, 2, 2), en la segunda circunferencia se van añadiendo los números intermedios, aquellos que eliminaríamos de la sucesión autosemejante, los que están en posiciones pares, ya que esta sucesión es de razón 2, pero manteniendo la posición de los números de la sucesión germen, lo cual se indica con un segmento radial. Es decir, si indicamos con corchetes los números añadidos, en la segunda circunferencia quedaría 0, [1], 1, [2], 1, [2], 2, [0], 1, [1], 2, [1], 2, [2], que genera dos copias de la sucesión germen, como se muestra en la siguiente imagen. Aunque podemos hacer una lectura de fuera hacia dentro, si en la segunda circunferencia eliminamos uno de cada dos números (por ser de razón 2), se obtiene la circunferencia interior.

Si ahora se añade la tercera circunferencia concéntrica exterior añadiendo de nuevo los números intermedios, se obtienen cuatro copias de la sucesión germen.

Si la sucesión autosemejante es de razón 3, como la que mostramos en la siguiente imagen (la sucesión germen es 0, 1, 2, 1, 2, 1, 2, 1), que es la central de la imagen que hemos mostrado arriba, entre dada dos números hay que incluir dos números (que son los excluidos en el proceso inverso).

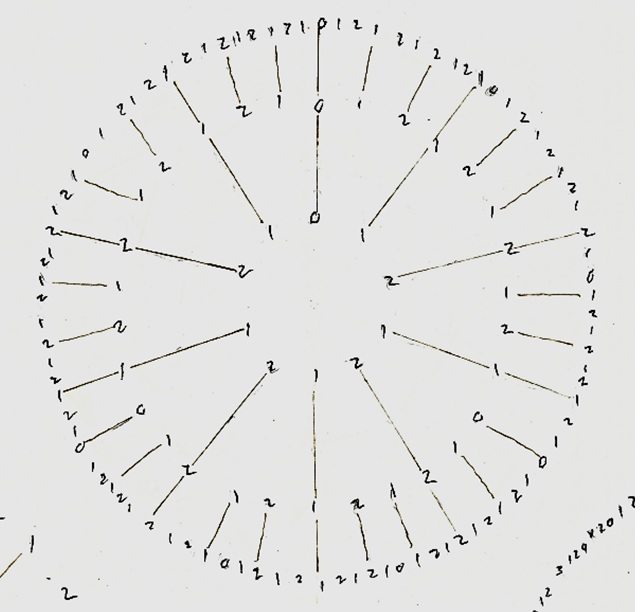
En mi opinión es una hermosa manera de representar las sucesiones autosemejantes, que surgen de una sucesión finita germen.

Mozart, como no…

Como escribe Emmanuel Amiot, en su artículo Self Similar Melodies, Tom Johnson “es probablemente el primer compositor que hizo uso de esto [la autosimilitud] de forma consciente y extensa, en obras como La vie est si court o Loops for orchestra”. Sin embargo, se pueden encontrar pequeños ejemplos de autosimilitud en obras más antiguas, como el conocido bajo Alberti (que es un tipo de acompañamiento repetitivo de cuatro notas, grave, agudo, medio, agudo -que en números podríamos representar como 1, 3, 2, 3-, que fue muy utilizado en el clasicismo, pero también en el romanticismo, que debe su nombre al compositor italiano Domenico Alberti (aprox. 1710/17 – 1740)) que se encuentra en el inicio de la Sonata para piano n. 16 en do mayor, K. 545 (1788) del gran Wolfgang Amadeus Mozart (1756-1791).

La sucesión infinita que se genera a partir de la repetición del motivo 1, 3, 2, 3 es autosemejante de razón 3 (también de razón 5 o cualquier otro número impar).

Bibliografía

1.- Tom Johnson, Rational Melodies, Editions 75, 1982.

2.- Tom Johnson, Self-similar Melodies, Editions 75, 2014.

3.- Tom Johnson, Finding Music, Writings 1961-2018, MusikTexte, 2019.

4.- Tom Johnson, Found Mathematical Objects, Seminaire Entretemps: Musique, Mathematiques et Philosophies, Paris, Ircam, 2001.

5.- Tom Johnson, Self-Similar Structures in my Music: an Inventory, lecture presented in the MaMuX seminar, IRCAM, Paris, 2006.

6.- Emmanuel Amiot, Auto Similar melodies, Journal of Mathematics and Music, vol. 3, n. 1, pp. 1-26, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica