El matemático Benoît Mandelbrot (1924- 2010) nació tal día como hoy, hace cien años. En un día tan especial, le dedicamos este retrato alfabético.

Autosimilitud

En matemáticas, la autosimilitud es la propiedad de un objeto (denominado autosimilar) en el que el todo es exactamente (como, por ejemplo, la curva de Koch) o aproximadamente similar (como en el caso del brócoli) a una parte de sí mismo. La autosimilitud es una propiedad de los conjuntos fractales.

Bourbaki

Aunque formado en Francia, los gustos científicos de Mandelbrot no encajaban con el enorme predominio de la escuela fundacional francesa de Bourbaki; por ello, en 1958, emigró a Estados Unidos de forma permanente.

Conjunto (de Mandelbrot)

Benoît Mandelbrot descubrió el conjunto que lleva su nombre en 1980; es un subconjunto del plano complejo.

Diferentes (aspectos y cosas)

En una entrevista realizada en 2004, Mandelbrot cuestionaba la aplicabilidad de la teoría fractal:

¿Cómo es posible que la misma técnica se aplique a Internet, al clima y a la bolsa? ¿Por qué, sin esforzarme demasiado, estoy tocando tantos aspectos diferentes de muchas cosas diferentes?

Escalamiento (en las finanzas)

A finales de los años 1980, Mandelbrot aplicó la teoría fractal al estudio de los mercados. Publicó varios trabajos sobre la ley de escalamiento en las finanzas, ley que ​muestra propiedades similares a distintas escalas de tiempo.

Fractal (Geometry of Nature)

En 1982 Mandelbrot publicó su libro Fractal Geometry of Nature en el que explicaba sus investigaciones en este área. En 1997 se publicó su traducción al español.

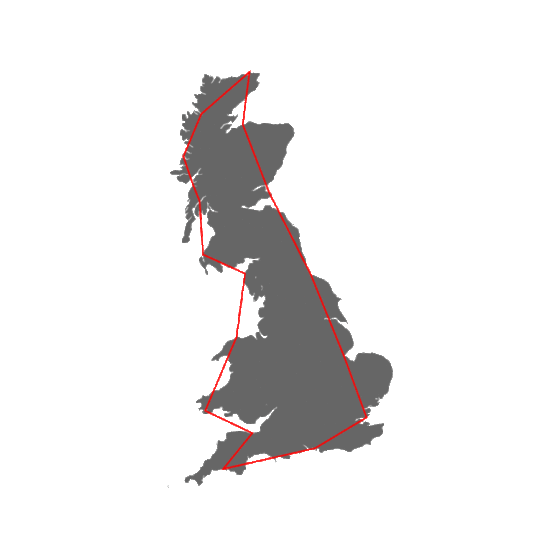
Gran (Bretaña)

En 1967 Mandelbrot publicó en la revista Science su famoso artículo ¿Cuánto mide la costa de Gran Bretaña? donde se exponen sus primeras ideas sobre los objetos fractales. El trabajo examina la paradoja de que la longitud de una línea costera depende de la escala de medida.

Hausdorff (dimensión)

La dimensión de Hausdorff generaliza el concepto de dimensión topológica y permite definir una dimensión no entera para un objeto fractal. Por ejemplo, la dimensión de Hausdorff del conjunto de Cantor es log(2)/log(3), que es aproximadamente 0,63.

IBM

Desde 1958, y durante 35 años, Mandelbrot trabajó en IBM.

Julia (conjuntos de)

Mandelbrot estudió los llamados conjuntos de Julia que son invariantes bajo ciertas transformaciones del plano complejo. Basándose en trabajos previos de los matemáticos Gaston Julia y Pierre Fatou, Mandelbrot representó gráficamente imágenes de estos conjuntos con ayuda de un ordenador.

Kagan (Aliette)

Mandelbrot se casó con Aliette Kagan en 1955 y se mudó a Ginebra para colaborar con Jean Piaget en el Centro Internacional de Epistemología Genética. En 1958, la pareja se mudó a Estados Unidos, donde Mandelbrot se unió al personal de investigación de IBM.

Lévy (Paul)

Tras realizar sus estudios en la Universidad de Lyon, en 1944, Mandelbrot ingresó en la École polytechnique donde fue tutorizado por el matemático Paul Lévy.

Mandelbrojt (Szolem)

Szolem Mandelbrojt, su tío, fue también matemático. Nació en Varsovia en 1899 en una familia judía procedente de Lituania. En 1920 emigró a Francia y en 1936 ayudó al resto de su familia a dejar Polonia para encontrarse con él. Influyó enormemente en la formación de su sobrino.

Nubes

En su libro Introduction to The Fractal Geometry of Nature, Mandelbrot escribió esta conocida frase sobre las formas geométricas en la naturaleza, comenzando por las nubes:

Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta.

Ordenadores

Gracias a su acceso a los ordenadores de IBM, Mandelbrot fue uno de los primeros en usar gráficos para crear y mostrar imágenes fractales como el conjunto de Mandelbrot y los conjuntos de Julia.

Precios

En sus primeros trabajos sobre mercados financieros, Mandelbrot descubrió que los cambios de precios no seguían una distribución gaussiana, sino distribuciones estables de Lévy con varianza infinita.

Rugosidad

Mandelbrot creó la primera «teoría de la rugosidad» al observar rugosidad en las formas de las montañas y costas, en las estructuras de las plantas, en los vasos sanguíneos y pulmones o en la agrupación de galaxias. Su deseo era establecer matemáticamente una medida de esa rugosidad.

Science

En esta revista, en 1967, publicó ¿Cuánto mide la costa de Gran Bretaña?.

Teoría (Big Bang vs. fractal)

Mandelbrot ofreció en 1974 una nueva explicación de la paradoja de Olbers (¿por qué la noche es oscura?). Postuló que, si las estrellas del universo estuvieran distribuidas de manera fractal (por ejemplo, como el conjunto de Cantor), no sería necesario recurrir la teoría del Big Bang para explicar la paradoja. Su modelo no descartaba un Big Bang, pero permitía un cielo oscuro incluso si el Big Bang no hubiera ocurrido.

Universidades

Fue profesor de diferentes materias en diferentes centros universitarios: impartió docencia en economía en la Universidad Harvard, en ingeniería en la Universidad de Yale, en fisiología en el Colegio Albert Einstein de Medicina y en matemáticas en París y Ginebra.

von Neumann

Mandelbrot defendió su tesis doctoral Contribution à la théorie mathématique des communications en la Universidad de París en 1952, supervisado por Paul Lévy. Después se fue al Instituto Tecnológico de Massachusetts y luego al Instituto de Estudios Avanzados de Princeton, donde fue el último estudiante de postdoctorado del matemático John von Neumann.

Wolf (premio)

Entre muchos otros galardones y reconocimientos, Mandelbrot recibió el Premio Wolf en física en 1993, ya que, según la Fundación Wolf, “al reconocer la aparición generalizada de fractales y desarrollar herramientas matemáticas para describirlos, ha cambiado nuestra visión de la naturaleza”.

XYZ (el final de su carrera y el final de este retrato alfabético)

Benoît Mandelbrot comentaba al final de su carrera:

Ahora que me acerco a los 80, me doy cuenta con melancólico placer de que, en muchas ocasiones estuve diez, veinte, cuarenta, incluso cincuenta años adelantado a mi tiempo.

Referencias

• J J O’Connor and E F Robertson, Benoit Mandelbrot, MacTutor History of Mathematics archive, University of St Andrews
• Benoît Mandelbrot, IBM
• Benoit Mandelbrot, Wikipedia

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia