Hace pocas semanas que me he leído las interesantes novelas gráficas Deep me (Salamandra Graphic, 2024) y Deep it (Salamandra Graphic, 2024), del escritor y dibujante de cómics francés Marc-Antoine Mathieu (1959), uno de los autores de cómics más vanguardista y estimulante de las últimas décadas.

Aunque estamos ante dos obras conectadas por una historia común, la primera entrega (Deep me) se trata de un thriller “existencialista” sobre la memoria, la identidad o lo que nos hace ser humanos, que arranca con su protagonista Adán que justo se despierta en una oscuridad total, sin recuerdo alguno, sin saber quién es, ni lo que le ha pasado e incapaz de comunicarse pese ser consciente de lo que sucede a su alrededor. Mientras que la segunda entrega (Deep it), en la que se deja de lado el thriller, se trata de un viaje de Adán en busca de respuestas sobre cuestiones fundamentales como lo que nos hace ser humanos, la conciencia, la vida y la muerte, la realidad o cómo puede ser el futuro de la humanidad.

Como comentábamos, Marc-Antoine Mathieu es un escritor y dibujante de cómics vanguardista y estimulante, con proyectos muy interesantes como la serie de cómics protagonizados por Julius Corentin Acquefacques (prisionero del revés), que por desgracia no ha sido publicada aún en español. En España, además de las dos obras mencionadas, se han publicado 3 segundos (Sins Entido, 2012) y Dios en persona (Salamandra Graphic, 2021), dos propuestas también muy originales, pero diferentes a las anteriores.

En español también nos encontramos con la edición de dos pequeñas, pero cautivadoras, obras, como son Laberintum y Mutación, publicadas por Rey Naranjo Editores, una editorial independiente de Colombia, dentro de su colección Bajotierra.

Precisamente, esta entrada del Cuaderno de Cultura Científica está relacionada con uno de esos dos cómics, Laberintum.

Laberintum

El cómic Laberintum, de Marc-Antoine Mathieu, fue publicado originalmente, en francés, en 2014. En la pequeña sinopsis de esta obra podemos leer lo siguiente.

Un hombre se enfrenta a un laberinto de pasillos que se va estrechando. A medida que avanza, él toma consciencia del funcionamiento de este mundo, Laberintum, que parece envolverlo todo alrededor suyo como un vicio.

Este es un cómic experimental que juega con la idea de la geometría fractal aplicada a un laberinto. Este laberinto con forma fractal ya puede intuirse en su portada, que vemos en la siguiente imagen.

El cómic empieza con el siguiente texto: “… Era una silueta apenas visible. La de un hombre. Ese hombre minúsculo era él mismo”. Y al texto le acompaña una viñeta única, a página completa, de ese extraño laberinto fractal en el que puede observarse un pequeño hombre, en uno de sus pasillos, que mira hacia la pared del laberinto.

Y sigue el siguiente texto, que nos adentra un poco más en la imagen y en la historia: “Desde su altura el hombre observaba pensativo, el laberintum. También él mismo parecía progresivamente estrecho, como los meandros que había recorrido”. Entonces, en la siguiente viñeta, también de página única, se produce un acercamiento al laberinto fractal y al personaje que se ve en el mismo, que le vemos apoyar la mano en la pared (véase la siguiente imagen).

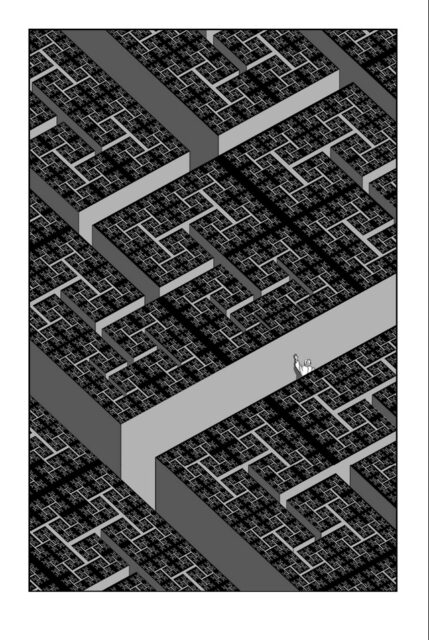
De hecho, en las siguientes viñetas, a página completa todas, se sigue produciendo un zoom sobre la imagen del laberinto y el personaje que se encuentra en el mismo, quien se sube a la pared del laberinto para observarlo desde arriba, que como podrá ver tiene una extraña forma fractal. Y esa forma fractal, que es el árbol fractal H, es la que vamos a explicar en esta entrada.

En las siguientes viñetas la imagen continúa con el zoom en el que se muestra al personaje más de cerca aún, observando el laberinto fractal, cuya estructura vemos que se repite (es la propiedad de autosemejanza del fractal), pero además llega un momento en el que él mismo descubre un pequeño personaje dentro del fractal, que según continua el zoom descubrirá que es él mismo, realizando los mismos movimientos que hemos observado en las viñetas anteriores. Por lo tanto, no solo el laberinto es autosemejante, ya que es un fractal, sino que la propia historia del cómic es autosemejante

Los fractales

Antes de entrar en la descripción del árbol fractal H, recordemos brevemente qué son los fractales. Estos son objetos matemáticos de una gran complejidad, pero no es sencillo dar una definición de los mismos, ya que todas las definiciones propuestas dejan algunos de los fractales fuera. El concepto de objeto fractal está ligado a tres de sus propiedades más características que, de forma breve y sencilla, explicamos a continuación:

1. Autosemejanza. Su estructura se repite a diferentes escalas. Si nos fijamos en una parte cualquiera de un objeto fractal y la ampliamos convenientemente (pensemos en la lupa de un ordenador o un microscopio) obtendremos una réplica del objeto fractal inicial. También podemos pensar en algunos objetos fractales como formados por copias de sí mismos a escalas más pequeñas.

La autosemejanza la podemos observar claramente en objetos fractales famosos como el conjunto de Cantor, la curva de Koch, la esponja de Menger (sobre los cuales podéis leer en la entrada Fractus, arte y matemáticas), las curvas de Hilbert, Peano y Sierpinski (que aparecen explicadas en la entrada La curva de Sierpinski, o sobre lo que esconden algunas obras de arte), el triángulo de Sierpinski (explicado en la entrada ¿Conocían los romanos el triángulo fractal de Sierpinski?) o el conjunto de Mandelbrot (que aparece en el cómic Promethea, como se explica en la entrada Guía matemática para el cómic ‘Promethea’).

1. Rugosidad. Los fractales son objetos geométricos de una gran rugosidad, de una gran irregularidad, y la medida matemática de esa rugosidad es la “dimensión fractal” (la dimensión de Hausdorff-Besicovich), que no explicaremos aquí por su complejidad. Los objetos de la geometría clásica (recta, circunferencia, esfera, …) son objetos lisos, sin rugosidad, y por lo tanto su dimensión es un número natural (la recta y las curvas tienen dimensión 1, las superficies 2, …), mientras que los fractales son objetos geométricos rugosos y su dimensión puede ser un número real no natural (las curvas fractales tienen dimensión entre 1 y 2, las superficies fractales entre 2 y 3, …).

De hecho, el conjunto de Cantor tiene dimensión fractal 0,6309…, la curva de Koch 1,2618…, el conjunto de Mandelbrot tiene dimensión fractal igual a 2 (este importante fractal no entraría dentro de la familia de fractales si la definición fuese que su dimensión es un número real no natural), la esponja de Menger 2,7268…, por citar algunos.

1. Procesos iterativos infinitos. Muchos de los objetos fractales son descritos mediante procesos iterativos, tanto geométricos, como analíticos, infinitos. Pongamos un ejemplo para ilustrarlo, la conocida curva de Koch.

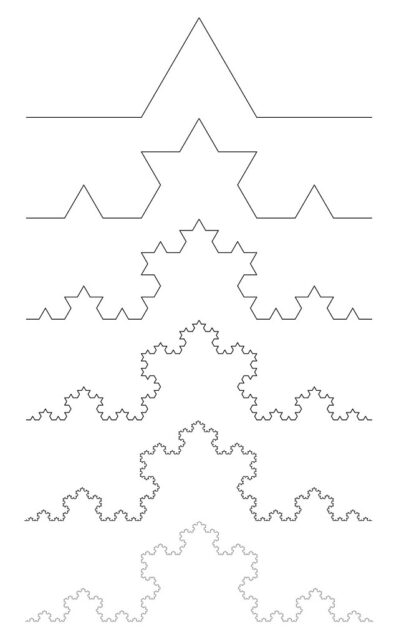
La curva de Koch fue introducida en 1904 por el matemático sueco Helge von Koch (1870-1924) como ejemplo de una curva continua que no tiene recta tangente en ningún punto. Para construir la curva de Koch, se empieza con un intervalo, por ejemplo, de longitud 1. En la primera iteración se divide el intervalo en tres partes, de longitud 1/3, y se reemplaza el intervalo central por dos segmentos de la misma longitud formando un ángulo de 60 grados entre ellos (como se ve en la imagen). La longitud total de la construcción en este primer paso es 4/3.

En la segunda iteración se realiza la misma operación en cada uno de los cuatro intervalos que se han formado en la primera. Obteniendo así una figura curva formada por 16 pequeños intervalos de longitud 1/9, luego la longitud total es 16/9 (4/3 al cuadrado). Y así se continúa en cada iteración. En el límite de este proceso infinito se obtiene la curva de Koch.

El árbol fractal H

El fractal H, o árbol fractal H, es el objeto fractal que utilizó el autor de cómics Marc-Antoine Mathieu en su obra Laberintum, en la cual se experimenta con la autosemejanza.

El árbol H es un fractal que se construye mediante un proceso iterativo infinito que se inicia con los segmentos correspondientes a una letra H mayúscula y, a continuación, colocando iterativamente Hs más pequeñas (reducidas a la mitad) centradas en la parte superior e inferior de cada segmento vertical libre. En la siguiente imagen podemos observar la H inicial (paso 1) junto con la imagen del paso 2 del proceso iterativo que consiste en colocar una H (como la anterior pero reducida a la mitad) en cada uno de los cuatro extremos de los segmentos laterales de la H grande.

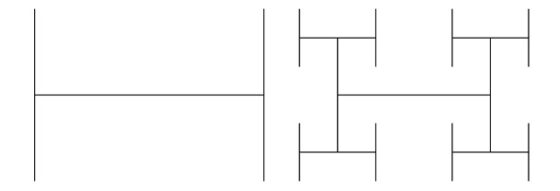
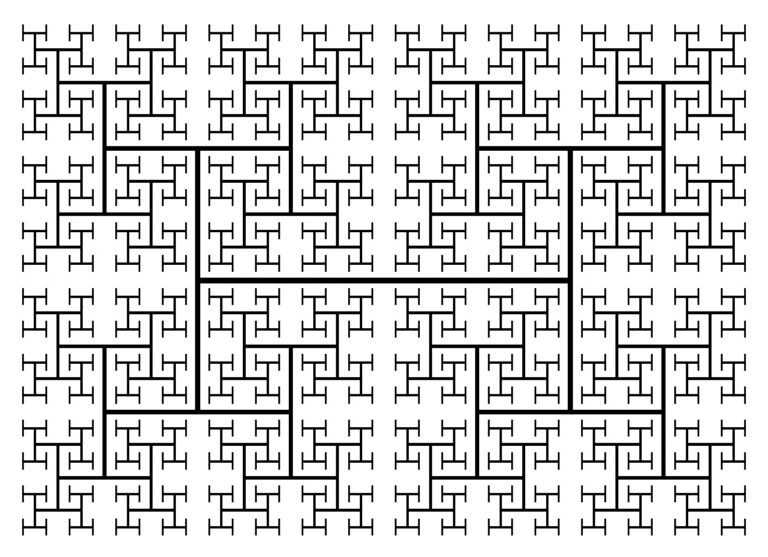
En la siguiente imagen observamos los resultados de los pasos 3 y 4 del proceso iterativo de construcción del árbol H. En el paso 3 se realizan 4 x 4 = 16 copias de la H, cuyo tamaño es la mitad del tamaño de las Hs del paso anterior, es decir, un cuatro del tamaño de la H original, que se colocan en los correspondientes extremos de los segmentos laterales de las cuatro Hs que se han incorporado en el paso anterior. Y en el paso 4 se colocan 4 x 16 = 64 copias de la H de la mitad de tamaño que las Hs incorporadas en el paso anterior.

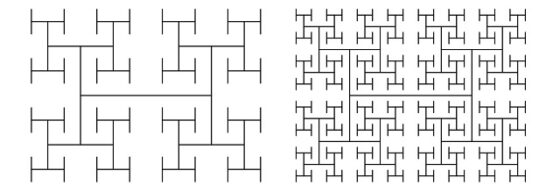
Siguiendo este proceso iterativo de forma infinita se obtiene el árbol fractal H.

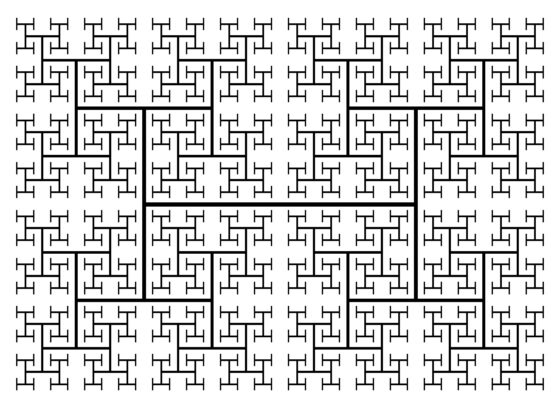
El árbol H es una “curva” de longitud infinita. Supongamos que la longitud de los segmentos de la H original (paso 1) fuese L. En el paso 2 se añaden cuatro copias que se han reducido a la mitad, luego la longitud del objeto obtenido en el paso 2 (la H junto con las cuatro copias de la mitad de tamaño) es igual a L + 4 (L / 2) = L (1 + 2) = 3 L.

En el paso 3 se añaden 16 copias cuyo tamaño es la cuarta parte que el tamaño de la H original. Por lo tanto, la longitud de este objeto es L + 4 (L / 2) + 16 (L / 4) = L (1 + 2 + 4) = 7 L.

En el paso 4 son 64 las copias de la H que se añaden a la estructura del paso anterior, cuyo tamaño es la octava parte del de la H original. En consecuencia, la longitud del objeto es ahora L + 4 (L / 2) + 16 (L / 4) + 64 (L / 8) = L (1 + 2 + 4 + 8) = 15 L.

Como podemos observar, en el paso n, nos quedaría la siguiente fórmula

es decir, la longitud es la longitud de la H original (L) multiplicado por el número de Mersenne 2ⁿ – 1. Por lo tanto, la longitud del árbol fractal H, que es el límite de la anterior sucesión de longitudes, es infinita.

Además, puede demostrarse que el árbol fractal H tiene dimensión fractal igual a 2.

Bibliografía

1.- V. Kaloshin, M. Saprykina (2012) An Example of a Nearly Integrable Hamiltonian System with a Trajectory Dense in a Set of Maximal Hausdorff Dimension Commun. Math. Phys. doi: 10.1007/s00220-012-1532-x

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica