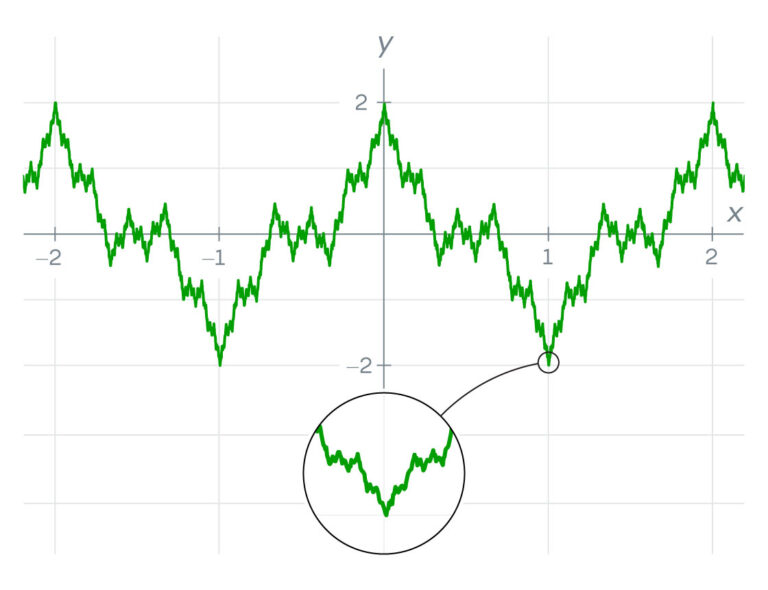
La monstruosa función dentada que rompió el cálculo
A finales del siglo XIX, Karl Weierstrass inventó una función similar a un fractal que fue tachada de «mal deplorable». Con el tiempo transformaría los fundamentos de las matemáticas.
Un artículo de Solomon Adams. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
El cálculo es una poderosa herramienta matemática. Sin embargo, durante cientos de años tras su invención en el siglo XVII, sus bases fueron precarias. Sus conceptos fundamentales se basaban en la intuición y en argumentos informales, más que en definiciones precisas y formales.
Como respuesta surgieron dos escuelas de pensamiento, según Michael Barany, historiador de las matemáticas y las ciencias de la Universidad de Edimburgo. Los matemáticos franceses, en general, se conformaban con seguir adelante. Estaban más interesados en aplicar el cálculo a problemas de física, utilizándolo para calcular las trayectorias de los planetas, por ejemplo, o para estudiar el comportamiento de las corrientes eléctricas. Pero, para el siglo XIX, los matemáticos alemanes comenzaron a desmantelar cosas. Se propusieron encontrar contraejemplos que socavaran suposiciones arraigadas, y finalmente utilizaron esos contraejemplos para asentar el cálculo sobre una base más estable y duradera.
Uno de estos matemáticos fue Karl Weierstrass. Aunque desde muy joven mostró aptitudes para las matemáticas, su padre lo presionó para que estudiara finanzas y administración públicas, con miras a convertirse en funcionario prusiano. Aburrido con sus estudios universitarios, se dice que Weierstrass pasaba la mayor parte del tiempo bebiendo y practicando esgrima; a finales de la década de 1830, tras no obtener su título, se convirtió en profesor de secundaria, impartiendo clases de todo tipo, desde matemáticas y física hasta caligrafía y gimnasia.
Weierstrass no comenzó su carrera como matemático profesional hasta que tuvo casi 40 años. Pero luego transformaría el campo al introducir un monstruo matemático.
Los pilares del cálculo
En 1872, Weierstrass publicó una función que ponía en peligro todo lo que los matemáticos creían comprender sobre el cálculo. Fue recibida con indiferencia, ira y temor, especialmente por los gigantes matemáticos de la escuela francesa. Henri Poincaré condenó la función de Weierstrass como «un ultraje al sentido común». Charles Hermite la calificó de «mal deplorable».
Para entender por qué el resultado de Weierstrass fue tan desconcertante, es útil comprender primero dos de los conceptos más fundamentales del cálculo: continuidad y diferenciabilidad.
Una función continua es exactamente lo que parece: una función sin saltos ni espacios. Puedes trazar una ruta desde cualquier punto de dicha función a cualquier otro sin necesidad de levantar el lápiz.
El cálculo consiste, en gran medida, en determinar la rapidez con la que cambian estas funciones continuas. Funciona, en términos generales, aproximando una función dada con líneas rectas no verticales.
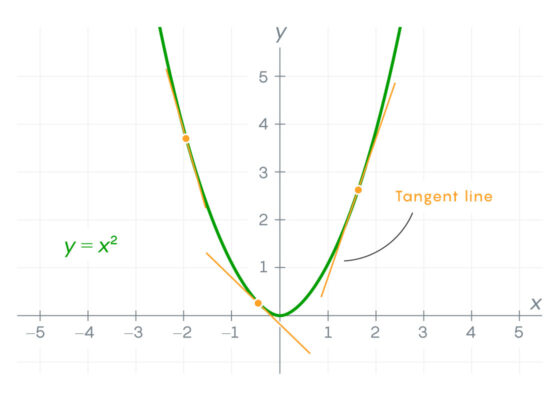
En cualquier punto de esta curva se puede dibujar una “tangente”, la línea que mejor se aproxima a la curva cerca de ese punto. La pendiente de la tangente mide la rapidez con la que cambia la función en ese punto. Se puede definir otra función, llamada derivada, que proporciona la pendiente de la tangente en cada punto de la función original. Si la derivada existe en cada punto, se dice que la función original es diferenciable.
Las funciones que contienen discontinuidades nunca son diferenciables: no se puede trazar una tangente que aproxime los huecos, lo que significa que la derivada no existirá en ellos. Pero incluso las funciones continuas no siempre son diferenciables en todos los puntos. Consideremos la función de «valor absoluto», que se ve así:
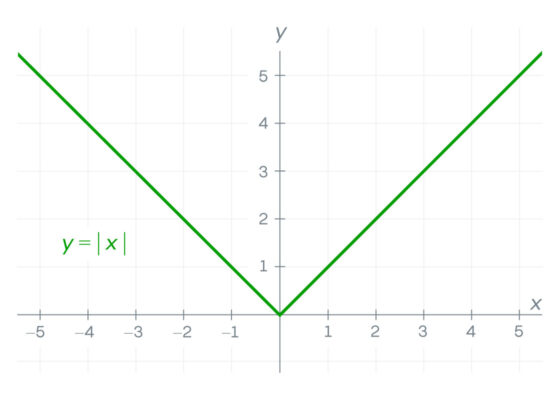
En el lado izquierdo de esta curva en forma de V, las rectas tangentes tienen pendiente descendente. En el lado derecho, tienen pendiente ascendente. En el vértice inferior, la pendiente cambia bruscamente de dirección. La derivada de la función no existe en ese punto, aunque esté bien definida en el resto.
Esto no inquietó a la mayoría de los matemáticos del siglo XIX. Lo veían como un fenómeno aislado: mientras la función sea continua, afirmaban, solo puede haber un número finito de puntos donde la derivada no esté definida. En todos los demás puntos la función debería seguir portándose bien y de forma uniforme. En otras palabras, una función solo puede zigzaguear hasta cierto punto.
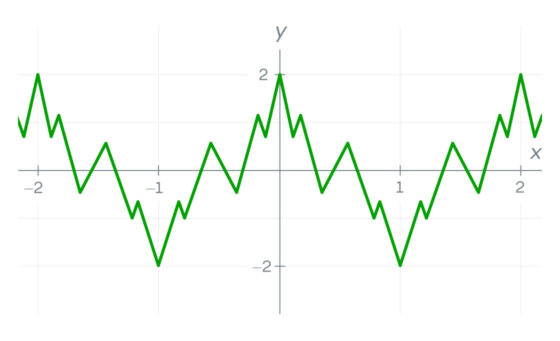
De hecho, en 1806, un destacado matemático y físico francés llamado André-Marie Ampère afirmó haber demostrado esto mismo. Durante décadas su razonamiento permaneció indiscutible. Entonces apareció Weierstrass.
El monstruo de Weierstrass
Weierstrass descubrió una función que, según la prueba de Ampère, debería haber sido imposible: era continua en todas partes, pero no diferenciable en ninguna.
La construyó sumando infinitas funciones «coseno» ondulatorias. Cuantos más términos añadía, más zigzagueaba su función, hasta que finalmente cambiaba de dirección abruptamente en cada punto, como un peine de dientes de sierra infinitamente dentado.
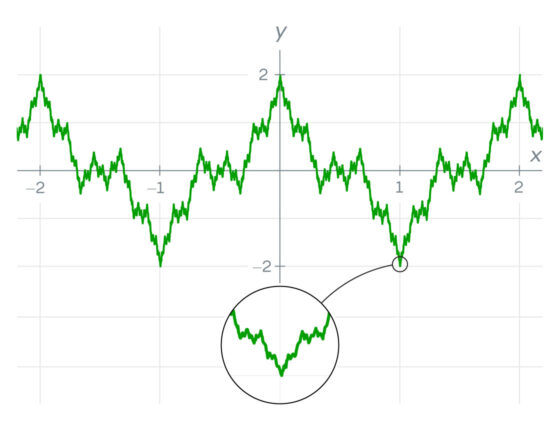
Muchos matemáticos descartaron la función. Era una anomalía, decían, obra de un pedante, matemáticamente inútil. Ni siquiera podían visualizarla. Al principio, al intentar trazar la gráfica de la función de Weierstrass, esta parece uniforme en ciertas regiones. Solo al ampliarla se verá que esas regiones también son irregulares, y que se volverán más irregulares y se comportarán mal (lo que los matemáticos llaman «patológicas») con cada aumento adicional.
Pero Weierstrass había demostrado sin lugar a dudas que, aunque su función no presentaba discontinuidades, nunca era diferenciable. Para demostrarlo, revisó primero las definiciones de «continuidad» y «diferenciabilidad» formuladas décadas antes por los matemáticos Augustin-Louis Cauchy y Bernard Bolzano. Estas definiciones se basaban en descripciones vagas y sencillas, y en una notación inconsistente, lo que facilitaba su malinterpretación.

Así que Weierstrass las reescribió, utilizando un lenguaje preciso y fórmulas matemáticas concretas. (Todo estudiante de cálculo aprende la definición épsilon-delta de un límite; fue Weierstrass quien introdujo la versión moderna y la utilizó como base para sus definiciones de continuidad y diferenciabilidad).
Entonces pudo demostrar que su función cumplía con su definición más rigurosa de continuidad. Al mismo tiempo, también pudo demostrar que, en cada punto, su nueva definición formal de la derivada de la función nunca tenía un valor finito; siempre “se disparaba” hasta el infinito. En otras palabras, la continuidad no implicaba diferenciabilidad. Su función era tan monstruosa como habían temido los matemáticos.
La prueba demostró que el cálculo ya no podía basarse en la intuición geométrica, como habían hecho sus inventores. Instauró un nuevo estándar para la disciplina, basado en el análisis minucioso de las ecuaciones. Los matemáticos se vieron obligados a seguir los pasos de Weierstrass, perfeccionando aún más su definición de funciones, su comprensión de la relación entre continuidad y diferenciabilidad, y sus métodos para calcular derivadas e integrales. Este trabajo para estandarizar el cálculo ha evolucionado hasta convertirse en el campo conocido como análisis; Weierstrass es considerado uno de sus fundadores.
Pero el legado de su función se extiende mucho más allá de los fundamentos del cálculo y el análisis. Reveló que las matemáticas están llenas de monstruos: funciones aparentemente imposibles, objetos extraños (es uno de los primeros ejemplos de fractal), comportamientos inusuales. «Existe todo un universo de posibilidades, y se supone que la función de Weierstrass nos abre los ojos a él», afirma Philip Gressman, de la Universidad de Pensilvania.
También resultó tener numerosas aplicaciones prácticas. A principios del siglo XX, los físicos querían estudiar el movimiento browniano, el movimiento aleatorio de partículas en un líquido o gas. Dado que este movimiento es continuo pero no uniforme —caracterizado por fluctuaciones rápidas e infinitamente pequeñas—, funciones como la de Weierstrass eran perfectas para modelarlo. De igual manera, estas funciones se han utilizado para modelar la incertidumbre en la toma de decisiones y la asunción de riesgos por parte de las personas, así como el complejo comportamiento de los mercados financieros.
Al igual que el propio Weierstrass, las consecuencias de su función a veces han tardado en manifestarse. Pero siguen moldeando las matemáticas y sus aplicaciones actuales.
El artículo original, The Jagged, Monstrous Function That Broke Calculus, se publicó el 23 de enero de 2025 en Quanta Magazine.
Traducido por César Tomé López