En medio del caos de la Francia revolucionaria, la obsesión matemática de un hombre dio paso a un cálculo que ahora sustenta gran parte de las matemáticas y la física. Este cálculo, llamado transformada de Fourier, descompone cualquier función en sus componentes.

Un artículo de Shalma Wegsman. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

Cuando escuchamos una pieza musical, nuestros oídos realizan un cálculo. El trino agudo de la flauta, los tonos medios del violín y el murmullo grave del contrabajo llenan el aire con ondas de presión de muy distintas frecuencias. Cuando la onda sonora combinada desciende por el canal auditivo hasta la cóclea en espiral, los cilios de distintas longitudes resuenan con los diferentes tonos, separando la señal confusa en compartimentos de sonidos elementales.

A los matemáticos les llevó hasta el siglo XIX dominar este mismo cálculo.

A principios del siglo XIX, el matemático francés Jean-Baptiste Joseph Fourier descubrió una manera de tomar cualquier función y descomponerla en un conjunto de ondas fundamentales, o frecuencias. Si volvemos a sumar esas frecuencias constituyentes, recuperamos la función original. La técnica, hoy conocida como la transformada de Fourier, permitió que este matemático —antiguo defensor apasionado de la Revolución francesa— provocara a su vez una auténtica revolución matemática.

De la transformada de Fourier nació todo un campo de las matemáticas: el análisis armónico, dedicado al estudio de los componentes de las funciones. Muy pronto, los matemáticos comenzaron a descubrir profundas conexiones entre el análisis armónico y otras áreas de las matemáticas y la física, desde la teoría de números hasta las ecuaciones diferenciales o la mecánica cuántica. También encontramos la transformada de Fourier en nuestros ordenadores, permitiendo comprimir archivos, mejorar señales de audio y mucho más.

“Es difícil exagerar la influencia del análisis de Fourier en las matemáticas”, comenta Leslie Greengard, de la Universidad de Nueva York y del Flatiron Institute. “Afecta prácticamente a todos los campos de las matemáticas, la física, la química y muchos otros”.

Llamas de pasión

Fourier nació en 1768 en medio del caos de la Francia prerrevolucionaria. Huérfano a los 10 años, fue educado en un convento de su ciudad natal, Auxerre. Pasó la siguiente década debatiéndose entre dedicar su vida a la religión o a las matemáticas, hasta que abandonó su formación religiosa y se convirtió en profesor. También participó activamente en los movimientos revolucionarios franceses hasta que, durante el Reinado del Terror en 1794, fue arrestado e ingresado en prisión a los 26 años por expresar ideas consideradas antirrevolucionarias. Estaba destinado a la guillotina.

Antes de su ejecución, sin embargo, el Terror llegó a su fin. Así, en 1795, pudo volver a la enseñanza de las matemáticas. Unos años más tarde fue nombrado consejero científico de Napoleón Bonaparte y se unió a su ejército en la invasión de Egipto. Fue allí, mientras investigaba también la antigüedad egipcia, donde inició el trabajo que le llevaría a desarrollar su transformada: quería comprender la matemática de la conducción del calor. Cuando regresó a Francia en 1801 —poco antes de que los británicos obligaran a retirarse al ejército francés y se quedaran con la piedra Rosetta— Fourier ya no podía pensar en otra cosa.

Si calentamos un extremo de una barra metálica, el calor se propagará hasta que toda la barra alcance la misma temperatura. Fourier sostenía que la distribución de calor en la barra podía escribirse como suma de ondas simples. A medida que el metal se enfría, estas ondas pierden energía, se suavizan y finalmente desaparecen. Las ondas de oscilación más rápida —con mayor energía— decaen primero, seguidas después por las de frecuencia más baja. Es como una sinfonía que se apaga gradualmente, desde los píccolos hasta las tubas.

La propuesta era radical. Cuando Fourier la presentó en 1807 ante el Instituto de París, el prestigioso matemático Joseph-Louis Lagrange declaró que aquello era “poco menos que imposible”.

Lo que más inquietaba a sus colegas eran los casos extraños en los que la distribución del calor pudiera ser bruscamente irregular, como una barra exactamente mitad fría y mitad caliente. Fourier defendía que esa discontinuidad de temperatura también podía describirse matemáticamente: bastaría con sumar infinitas curvas simples en lugar de un número finito. Pero la mayoría de los matemáticos de la época creía que ninguna cantidad de curvas suaves podía producir un ángulo brusco.

Hoy sabemos que, en lo esencial, Fourier tenía razón.

“Se puede representar cualquier cosa como suma de estas oscilaciones muy, muy simples”, explica Charles Fefferman, matemático de la Universidad de Princeton. “Se sabe que, si uno tiene suficientes diapasones y los hace sonar de forma precisa, pueden reproducir la Novena Sinfonía de Beethoven”. El proceso solo falla para funciones extremadamente extrañas, como aquellas que oscilan salvajemente por mucho que se amplíe su gráfica.

Un oído entrenado

Realizar una transformada de Fourier es como oler un perfume y distinguir sus ingredientes, o escuchar un acorde de jazz complejo y reconocer las notas que lo componen.

En términos matemáticos, la transformada de Fourier es una función. Toma como entrada una función dada —que puede tener un aspecto muy complicado— y produce como salida un conjunto de frecuencias. Si escribimos las ondas seno y coseno correspondientes a esas frecuencias y las sumamos, recuperaremos la función original.

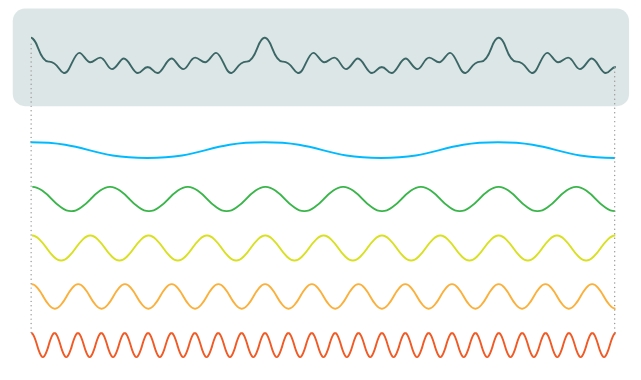
Para lograrlo, la transformada de Fourier examina todas las posibles frecuencias y determina cuánto contribuye cada una a la función original. Veamos un ejemplo sencillo.

Consideremos la siguiente función:

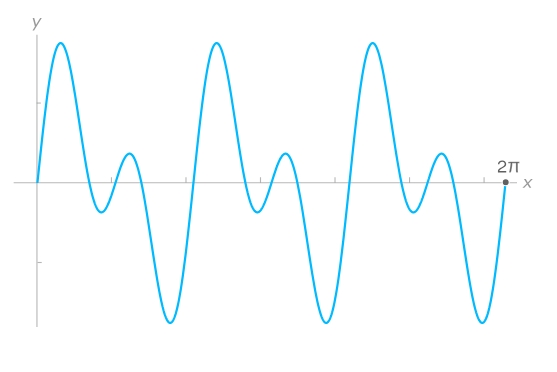
La transformada de Fourier comprueba cuánto aporta cada frecuencia a esta función original. Lo hace multiplicando ondas entre sí. Esto es lo que ocurre al multiplicar la función original por una onda seno de frecuencia 3:

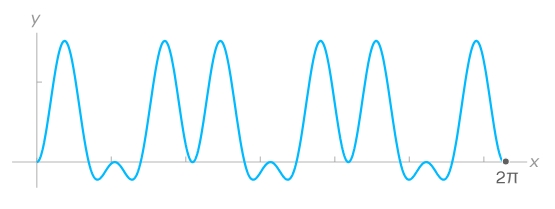
Aparecen picos muy grandes, lo que indica que la frecuencia 3 contribuye a la función original. La altura media de esos picos revela la magnitud de su contribución.

Ahora probemos con la frecuencia 5. Esto es lo que obtenemos al multiplicar la función original por una onda seno de frecuencia 5:

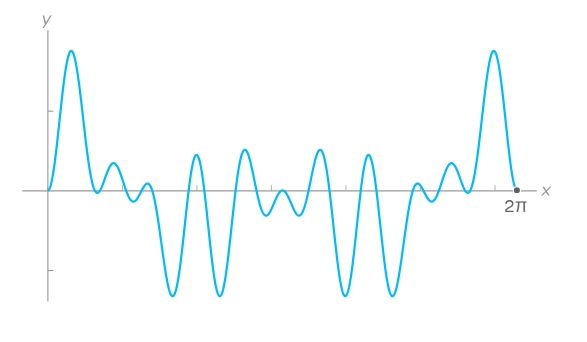
En este caso hay grandes picos pero también grandes valles, de modo que el gráfico se promedia alrededor de cero. Esto indica que la frecuencia 5 no contribuye a la función original.

La transformada de Fourier repite este procedimiento con todas las frecuencias posibles, multiplicando la función original por ondas seno y coseno. (En la práctica, este análisis se realiza en el plano complejo, combinando números reales e imaginarios).

De esta manera, la transformada de Fourier puede descomponer una función complicada en apenas unos pocos números. Por eso se ha convertido en una herramienta crucial para los matemáticos: cuando un problema parece insoluble, pueden intentar transformarlo. Con frecuencia, traducirlo al lenguaje de las frecuencias lo simplifica enormemente.

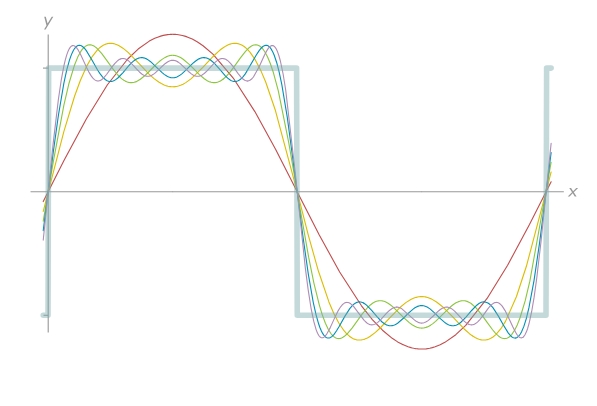
Si la función original tiene un borde brusco, como la onda cuadrada que suele aparecer en las señales digitales, la transformada de Fourier producirá un conjunto infinito de frecuencias que, al sumarse, aproximan ese borde lo mejor posible. Este conjunto infinito se llama serie de Fourier y —pese a la reticencia inicial de los matemáticos a aceptarla— hoy es una herramienta esencial en el análisis de funciones.

Bis

La transformada de Fourier también se aplica a objetos de más dimensiones, como las imágenes. Podemos pensar en una imagen en escala de grises como una función bidimensional que indica el brillo de cada píxel. La transformada de Fourier descompone esa función en un conjunto de frecuencias bidimensionales. Las ondas seno y coseno definidas por esas frecuencias forman patrones de rayas en distintas direcciones. Estos patrones —y combinaciones sencillas de ellos que recuerdan a un tablero de ajedrez— pueden sumarse para reconstruir cualquier imagen.

Por ejemplo, cualquier imagen de 8 × 8 puede componerse a partir de una combinación de los 64 bloques básicos siguientes. Un algoritmo de compresión puede entonces eliminar la información de alta frecuencia, correspondiente a los pequeños detalles, sin cambiar demasiado el aspecto de la imagen para el ojo humano. Así es como los JPEG logran comprimir imágenes complejas en datos mucho más reducidos.

En la década de 1960, los matemáticos James Cooley y John Tukey idearon un algoritmo que permitía realizar una transformada de Fourier mucho más rápido: la transformada rápida de Fourier (FFT, por sus siglas en inglés). Desde entonces, la transformada de Fourier se aplica prácticamente cada vez que hay una señal que procesar. “Hoy forma parte de la vida cotidiana”, comenta Greengard.

Se ha utilizado para estudiar las mareas, detectar ondas gravitacionales y desarrollar el radar y la resonancia magnética. Nos permite reducir el ruido en archivos de audio saturados y comprimir y almacenar todo tipo de datos. En mecánica cuántica —la física de lo muy pequeño— incluso proporciona el fundamento matemático del principio de incertidumbre, que afirma que es imposible conocer con precisión simultánea la posición y el momento lineal de una partícula. Podemos escribir una función que describa las posiciones posibles de una partícula; la transformada de Fourier de esa función describirá los momentos posibles de la partícula. Si la función indica con alta probabilidad la posición de la partícula —representada por un pico agudo en su gráfica—, entonces su transformada de Fourier estará muy dispersa. Será imposible determinar su momento. Lo contrario también es cierto.

La transformada de Fourier ha echado raíces en toda la investigación matemática pura. El análisis armónico —que estudia la transformada de Fourier y también cómo invertirla para reconstruir la función original— es un marco poderoso para estudiar ondas. Los matemáticos han descubierto además conexiones profundas e inesperadas con la teoría de números. Gracias a ellas han podido explorar relaciones entre los números enteros, incluida la distribución de los números primos, uno de los mayores misterios de las matemáticas.

“Si la gente no conociera la transformada de Fourier, no sé qué porcentaje de las matemáticas desaparecería”, afirma Fefferman. “Pero sería un porcentaje muy grande”.

El artículo original, «What Is the Fourier Transform?«, se publicó el 3 de septiembre de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.

Traducido por César Tomé López