Una apuesta engañosa
A Julene, como buena bilbaína, le encanta hacer apuestas.
Está en clase de geografía, un tanto aburrida, escuchando al profesor López que está explicando el funcionamiento de las redes hidrográficas terrestres. Para intentar vencer la apatía, propone a su compañero de pupitre, Mikel, apostar sobre los números que va a mencionar el docente a lo largo de su lección. Así, Julene invita a Mikel a apostar diez euros en un juego que tratará sobre los siguientes nueve números que mencionará el profesor, números que hacen referencia a longitudes (en kilómetros) de ríos u otras corrientes fluviales.

Julene propone las reglas del juego a Mikel
Julene comenta los términos de la apuesta a Mikel:
Te propongo tener en cuenta únicamente la primera cifra significativa de las longitudes de los cursos de agua que mencione el profesor. Yo me quedaré con el conjunto de las tres primeras cifras A = {1, 2, 3} y tú con el conjunto de las otras seis cifras B = {4, 5, 6, 7, 8, 9}. Ganará, y recibirá los diez euros del otro, quien tenga en su conjunto la primera cifra que haya aparecido con mayor frecuencia en la lección.
Para aclarar su propuesta, Julene continúa argumentando para convencer a Mikel de que está siendo generosa con él:
Si las nueve longitudes mencionadas son, por ejemplo, 243 km, 876 km, 1222 km, 92 km, 4330 km, 982 km, 3445 km, 2122 km y 832 km (cuyos primeros dígitos son 2, 8, 1, 9, 4, 9, 3, 2 y 8), tú ganarías porque en el anterior listado de primeros dígitos hay cinco números del conjunto B, el tuyo, y sólo cuatro del conjunto A, el mío.
Julene es una jugadora astuta y, con su propuesta de juego y el ejemplo que hábilmente ha expuesto, ha conseguido que Mikel crea que es sencillo para él ganar los diez euros de la apuesta. Al fin y al cabo, el conjunto que le corresponde (el conjunto B) tiene seis dígitos y el de Julene (el conjunto A) solo posee tres. Así que, convencido de que tiene muchas posibilidades de ganar los diez euros, Mikel acepta el juego de Julene.
Pero se equivoca; de hecho, Julene tiene una mayor probabilidad de ganar. ¿Cómo puede ser esto cierto?
Con las reglas de Julene, a Mikel no le conviene jugar
Efectivamente, Julene ha conseguido embaucar a Mikel; con sus reglas, ella sabe que tiene bastantes probabilidades de quedarse con los diez euros de su compañero.
La explicación de la ventaja de Julene en este juego tiene que ver con la llamada ley de Benford (o ley del primer dígito) que se refiere a una distribución de frecuencia estadística observada empíricamente en muchas fuentes de datos numéricos (como en el caso de la medida de la longitud de ríos). Esta ley dice que la cifra 1 aparece en primera posición con mucha mayor frecuencia que el resto de los números. Además, según crece el primer dígito, es menos probable que se encuentre en la primera posición.
La ley de Benford establece que la probabilidad de que un número obtenido de un determinado dato comience con el dígito d es de:
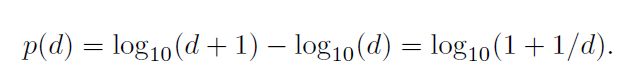
En la práctica, la frecuencia de aparición de cada número es de:
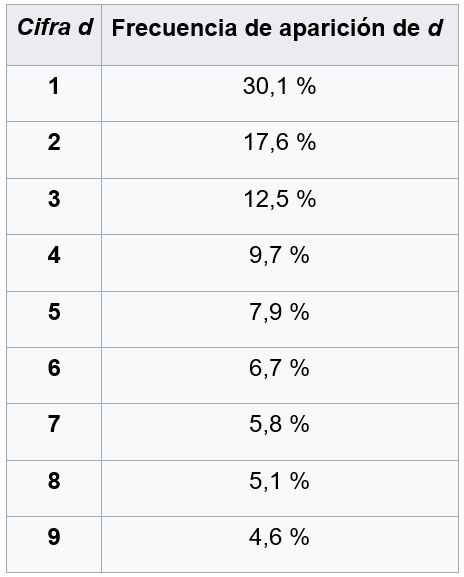
Si la apuesta consistiera en jugar con un único número, Julene ganaría con una probabilidad de a = p(1) + p(2) + p(3) = 0,602 (0,301 + 0,176 + 0,125 = 0,602). Por lo tanto, Mikel ganaría con una probabilidad de b = 1 – a = 0,398.
Pero la apuesta tiene en cuenta nueve números, no solo uno. Así, la probabilidad de que Julene gane es la probabilidad de que, entre los nueve números que mencionará el profesor durante su clase, haya al menos cinco (cinco, seis, siete, ocho o nueve números) pertenecientes al conjunto A = {1, 2, 3}. Dicho de otro modo, de los números significativos mencionados por el docente, como mucho cuatro pertenecerán al conjunto B = {4, 5, 6, 7, 8, 9} asignado a Mikel, que perdería así la apuesta.
La probabilidad de que haya k números de A = {1, 2, 3} entre los nueve números utilizados por el profesor (probabilidad de k éxitos en una repetición de 9 experimentos) es de:
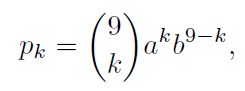
que involucra un coeficiente binomial (cantidad de subconjuntos de k elementos escogidos de un conjunto de 9 elementos).
Así, la probabilidad de que Julene gane es de:
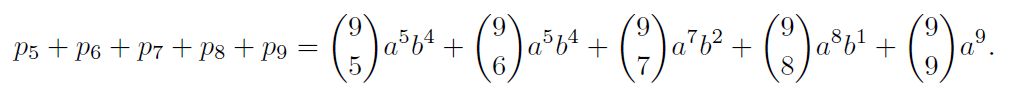
Tras hacer las operaciones indicadas en la anterior fórmula, el resultado es de 0,738. Así, Mikel tiene pocas probabilidades de ganar (1 – 0,738 = 0,262), y muchas de perder los diez euros de la apuesta… ¡Su compañera Julene “se la ha jugado”!
Nota
Adaptado de: Jean-Paul Delahaye, Rubrique des paradoxes précédents : La longueur des fleuves, Accromath 20.2 été-automne 2025
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
