Desde hace mucho tiempo, una de las novelas que habitaba el tsundoku de la mesilla colocada al lado de mi cama era Apeirógono (2020, en España 2021), del escritor irlandés Colum McCann, esperando su turno y el mejor momento para ser leída, que se iba posponiendo una y otra vez por diferentes motivos. Llegué a esta novela por casualidad. Investigando sobre obras literarias en las que aparecieran los números amigos, en particular, la pareja 220 y 284, me encontré con esta novela. Leí la sinopsis, que me pareció muy interesante, me la compré inmediatamente y ocupó su lugar en el tsundoku de mi mesilla, hasta hace poco que decidí que ya era hora de leerla.

En esta entrada del Cuaderno de Cultura Científica vamos a adentrarnos en la novela y en las cuestiones matemáticas que aparecen, directa o indirectamente, en la misma.

Colum McCann, escritor de la empatía

Colum McCann es un escritor irlandés, nacido en Dublín en 1965, que en la actualidad vive en Nueva York. Hasta la fecha ha escrito ocho novelas, desde Perros que cantan (1995, en español en 2021), hasta Twist (2025), pasando por Que el vasto mundo siga girando (2009, en español en 2010), galardonada, entre otros reconocimientos, con el National Book Award de EE. UU. y el Dublin IMPAC Prize, Transatlántico (2013, en español 2014) o la protagonista de esta entrada Apeirógono; tres colecciones de relatos, entre ellas Trece formas de mirar (2015, en español en 2017), cuyo cuento Shjol fue galardonado con el Pushcart Prize; así como dos libros de no ficción, que son la colección de ensayos 50 consejos para ser escritor (2017, en español en 2018) y el libro American Mother (2024), escrito junto a Diane Foley, cuyo hijo, el periodista James Foley, fue capturado y asesinado por ISIS. Ha recibido muchos reconocimientos a lo largo de su carrera como escritor, por ejemplo, nombrado Caballero de las Artes y las Letras por el gobierno francés (2009), elegido miembro de la Academia Irlandesa de Artes Aosdána (2009) y de la Academia Estadounidense de las Artes y las Letras (2017).

Colum McCann es uno de los miembros fundadores de la organización mundial sin ánimo de lucro Narrative 4, formada por escritores, artistas, educadores y activistas sociales. Narrative 4 utiliza la narración personal para fomentar la empatía entre los jóvenes, con el fin de que puedan mejorar juntos sus comunidades, pero también el mundo. En palabras del escritor, “ponerse en el lugar de los demás para poder volver al nuestro, a través de nuestras historias, es una experiencia poderosa y sanadora”.

Y para terminar esta pequeña presentación del escritor irlandés, recogemos las siguientes declaraciones de McCann:

Creo en la democracia de la narración. Me encanta el hecho de que nuestras historias puedan traspasar todo tipo de fronteras y límites. Me siento honrado por la idea de formar parte, aunque sea de forma mínima, de la experiencia literaria. Crecí en una casa, en una ciudad, en un país moldeado por los libros. No conozco mayor privilegio que el de poder contar una historia o escuchar una historia. Son lo único que tenemos que puede superar a la vida misma.

Apeirógono, una novela para la paz

La novela Apeirógono, del escritor irlandés Colum McCann, fue publicada originalmente en 2020 (en España fue publicada por Seix Barral en 2021) y rápidamente se convirtió en un auténtico éxito de crítica y ventas. Recibió muchos reconocimientos internacionales como el Premio a la mejor novela extranjera de Francia, el Premio Montluc Résistance et Liberté (Francia), el Premio Nacional del Libro Judío de Estados Unidos, entre otros; además, fue finalista de prestigiosos premios como el Premio Booker (Gran Bretaña), Premio IMPAC de Dublín (Irlanda) o el Premio Orwell de ficción política (Gran Bretaña); así mismo fue considerado mejor libro del año por prestigiosas publicaciones como The Guardian, The New York Times, The Washington Post o The Sunday Times.

La novela, basada en una historia real, se centra en la vida de dos hombres, el israelí Rami Elhanan y el palestino Bassam Aramin, cuyas hijas murieron como consecuencia del conflicto israelí-palestino. El diseñador gráfico israelí Rami Elhanan perdió a su hija Smadar, de casi 14 años, en un atentado terrorista perpetrado por tres suicidas palestinos. Como el personaje de Rami narra en la novela:

Aquel día, en 1997, tres suicidas con bombas se volaron por los aires en medio de la calle Ben Yehuda, en el centro de Jerusalén, tres bombas, una detrás de otra. Mataron a ocho personas: a ellos mismos y a otras cinco, incluidas tres niñas. Una de esas niñas era nuestra Samadari. Era jueves, las tres de la tarde. Estaba fuera comprando libros para el colegio y luego iba a apuntarse a clases de baile. Un bonito día tranquilo. Iba por la calle con sus amigas escuchando música.

Mientras que el académico y antiguo preso político palestino Bassam Aramin perdió a su hija Abir, de 10 años, por el impacto de una bala de goma disparada por un policía israelí. En palabras del personaje de Bassam en la novela:

Pero el 16 de enero de 2007 –dos años después de que fundase Combatientes por la Paz–, mi hija de diez años Abir salió del colegio a primera hora de la mañana. Era un día tranquilo, aquel Martes Negro mío, no pasaba gran cosa. Estaba cerca de las puertas del colegio cuando le disparó un miembro de la policía fronteriza israelí. Con una bala de goma. Una bala de goma de fabricación estadounidense. Un M-16 de fabricación estadounidense. Desde un todoterreno de fabricación estadounidense. No había violencia ni ninguna intifada en marcha. Le dispararon. En la parte posterior del cráneo. Venía de la tienda. Se acababa de comprar unos caramelos.

Aunque la novela se centra en Bassam y Rami, también son protagonistas de la misma Nurit Peled-Elhanan, madre de Smadar, y Salwa Aramin, madre de Abir. Nurit Peled-Elhanan es filóloga, escritora, traductora y activista pacifista israelí, con una participación muy activa también en el Círculo de Padres – Foro de Familias (PCFF), del que hablaremos a continuación, y ha recibido el Premio Sájarov a la Libertad de Conciencia del Parlamento Europeo en 2001. Por su parte, la palestina Salwa Aramin, también participa en las actividades del Círculo de Padres – Foro de Familias, aunque siempre ha intentado mantener un perfil menos público.

En 2005, doce soldados israelíes que se habían negado a servir en los territorios ocupados se reunieron con cuatro excombatientes palestinos, la mayoría de ellos del movimiento Fatah, con el objetivo de iniciar un camino de no violencia, de diálogo y entendimiento que llevase a la paz entre israelíes y palestinos. En ese grupo inicial del movimiento Combatientes por la Paz (que se constituiría formalmente en 2006) estaban el palestino Bassam Aramin y el israelí Elik Elhanan, el hijo mayor de Rami Elhanan, que cumplía el servicio militar obligatorio cuando su hermana Smadar murió en el atentado. Poco después se uniría Rami a Combatientes por la Paz, encontrándose allí con Bassam.

Por otra parte, el Círculo de Padres – Foro de Familias (PCFF) es una organización que incluye a familias palestinas e israelíes que han perdido a un ser querido debido al conflicto. Fue fundada en 1995, primero con familias israelíes, a las que se unieron familias palestinas en 1998. Rami Elhanan y Bassam Aramin, quienes ingresaron en el Círculo de Padres poco después de los asesinatos de sus hijas, son dos de sus miembros más activos y conocidos.

El camino de no violencia que Bassam y Rami emprendieron por la paz, primero en Combatientes por la Paz y luego en Círculo de Padres, desde donde han llevado la historia de sus hijas Abir y Smadar por todo el mundo, con el objetivo de acabar con el conflicto israelí-palestino, los ha llevado a entablar una fuerte amistad entre ambos, una amistad de “hermanos”.

Como dice Bassam en una entrevista:

Somos hermanos. Nuestra relación está por encima del conflicto porque compartimos el mismo tipo de valores. Nos preocupamos por los seres humanos, nos preocupamos por los civiles, nos preocupamos por la democracia y la libertad.

Apeirógono, un título geométrico

Si nos vamos a un libro clásico de geometría euclidiana como es Geometry Revisited (1967), de los matemáticos Harold Scott M. Coxeter y Samuel L. Greitzer, en el mismo se explica que un polígono puede definirse como “un conjunto de puntos (denominados vértices) y un número igual de segmentos rectos (denominados lados o aristas), es decir, un conjunto de puntos ordenados cíclicamente en un plano, sin tres puntos sucesivos colineales, junto con los segmentos de línea que unen pares consecutivos de los vértices. En otras palabras, un polígono es una línea discontinua cerrada que se encuentra en un plano”. En función del número de lados se hablará de triángulo, cuadrilátero, pentágono, hexágono, etcétera. Nótese, que en la anterior definición se está asumiendo que el polígono está formado por un número finito de puntos y lados.

Además, un polígono se dice que es regular si todos sus lados tienen la misma longitud (se dice que el polígono es equilátero) y todos sus ángulos son iguales, miden lo mismo (se dice que el polígono es equiangular). Los polígonos pueden ser convexos o estrellados.

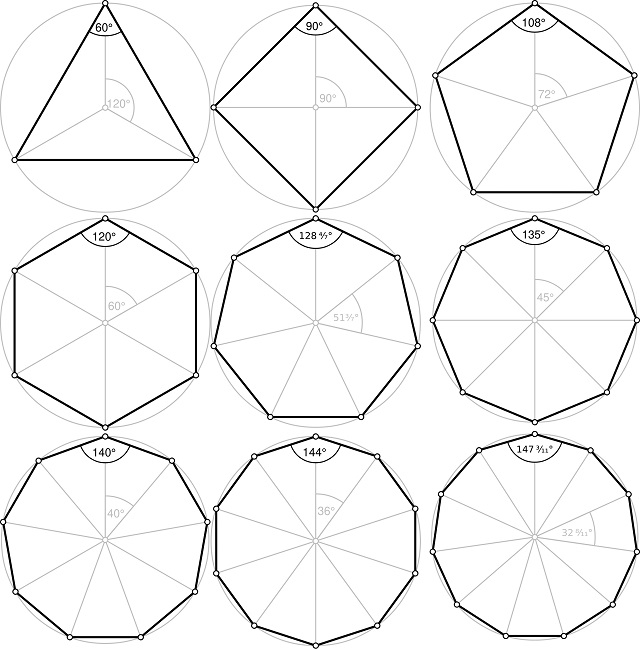
Si se va incrementando el número de lados de los polígonos regulares (convexos), en el límite, pueden ocurrir una de las dos siguientes cosas. Si se mantiene el radio de los polígonos (la distancia del centro a cualquiera de los vértices), según va aumentando el número de lados de los polígonos, estos se van aproximando a una circunferencia, del mismo radio que los polígonos.

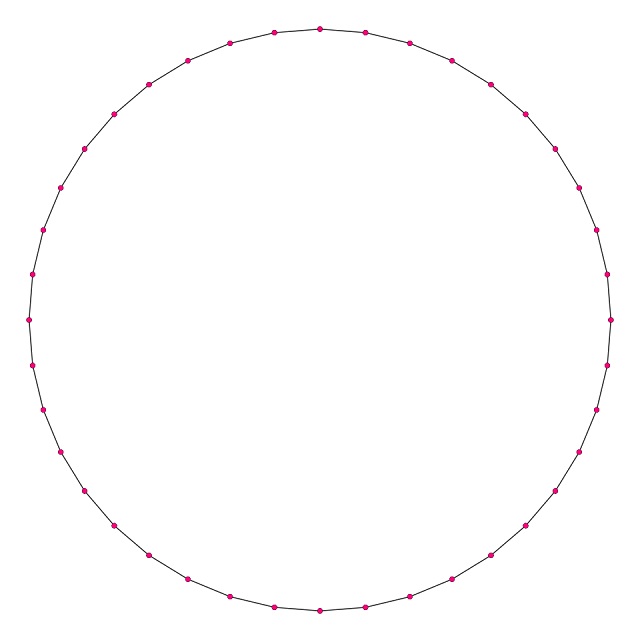
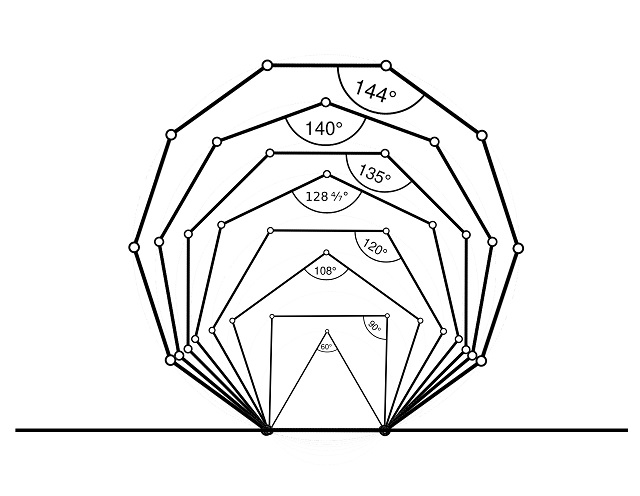
Mientras que, si los polígonos tienen el mismo lado, es decir, la longitud de sus lados es la misma para todos los polígonos, según se va aumentando el número de lados de los polígonos, estos se van aproximando a un apeirógono regular, a una recta infinita formada por vértices equidistantes y los segmentos entre ellos.

Un apeirógono regular es un polígono regular con un número infinito (numerable) de lados.

El matemático croata-israelí Branko Grünbaum descubrió dos nuevos polígonos infinitos regulares, el polígono en zig-zag

y el polígono, fuera del plano (tridimensional), con forma de hélice

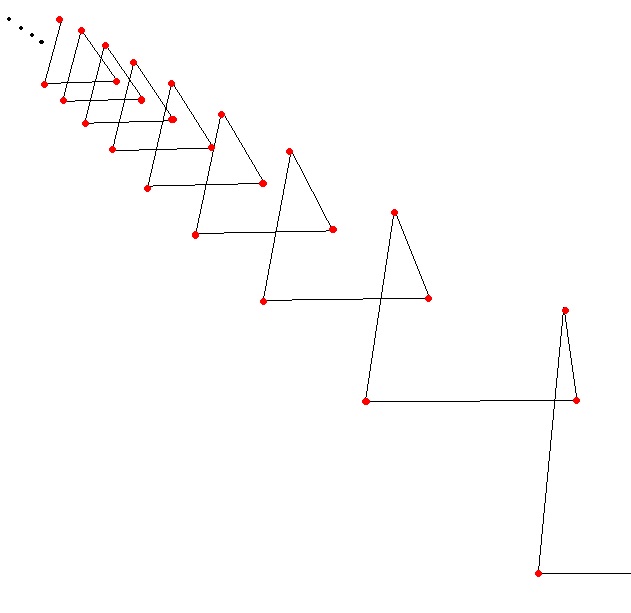
También existen apeirógonos cerrados, pero no regulares. Por ejemplo, se consideran sus vértices sobre una circunferencia, de manera que por cada lado convergen a un mismo punto de la circunferencia (punto de acumulación).

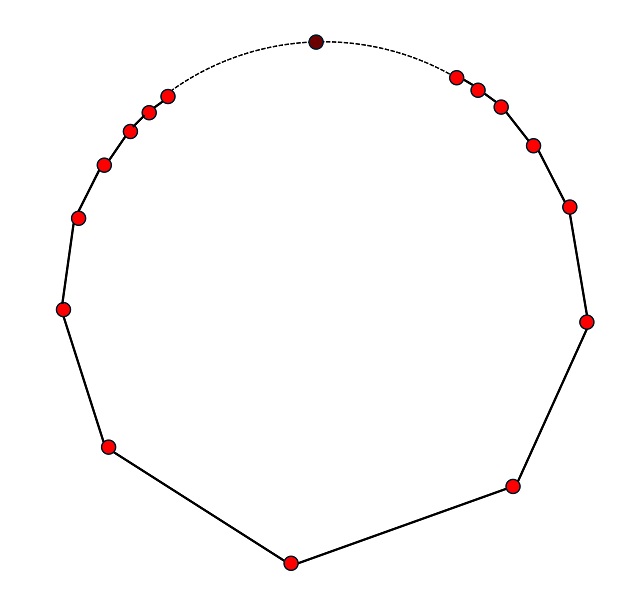
Aunque, según algunas definiciones de polígono infinito, como la de Branko Grünbaum, el anterior ejemplo no sería un polígono infinito, ya que se le pide que dentro de cualquier circunferencia que se trace en el plano tiene que tener un número finito de vértices y aristas.

Pero vayamos a la novela que nos ocupa. La primera cita en la que aparece el término apeirógono, después del título, es la siguiente.

181

Apeirógono: polígono con un número contablemente infinito de lados.

182

Lo contablemente infinito es la forma más simple de la infinidad. Si comenzamos por el cero, podemos usar números naturales para contar de manera consecutiva y, aunque la cuenta se prolongue por toda la eternidad, podemos llegar a cualquier punto del universo en una cantidad finita de tiempo.

Podemos preguntarnos por la intención del autor de la novela al ponerle como título el término geométrico “apeirógono”. El motivo es que McCann quiere expresar con el mismo que el conflicto israelí-palestino es muy complejo, tiene muchas aristas y se puede mirar desde diferentes (infinitas) perspectivas, como así intenta reflejarlo en el libro con la estructura, de la que hablaremos a continuación.

Una estructura simétrica

Esta novela tiene una fuerte inspiración en la recopilación de cuentos populares de Oriente Medio Las mil y una noches, de hecho, podemos decir que es un homenaje a la misma. Más aún, esta obra se cita en varias ocasiones a lo largo de la novela Apeirógono.

Además, la obra se divide en 1.001 pequeños capítulos, a lo largo de los cuales, no solo se narra la historia de Bassam y Rami, sino que se incluyen muchos otros relatos culturales, que van desde la ornitología, la música, la literatura, la arquitectura, el arte, la química, la geografía, la historia o la religión, e incluso, las matemáticas.

280

En un artículo de 1940, G. H. Hardy escribió: “Los esquemas de los matemáticos, al igual que los de los pintores y de los poetas, tienen que ser bellos; las ideas, como los colores o las palabras, tienen que encajar entre ellas de una manera armoniosa. La belleza es la primera prueba: no hay un lugar permanente en el mundo para las matemáticas feas”.

Colum McCann ha dividido la novela en 1.001 breves capítulos distribuidos de forma simétrica, primero del 1 al 500, después el 1.001, para continuar del 500 al 1. Esta estructura nos remite a la simetría. Las historias del palestino Bassam y el israelí Rami, la pérdida de sus hijas, su dolor, su lucha por la paz, su humanidad, son simétricas. Además, el capítulo 1.001 está en el centro (eje de simetría), simboliza el punto de encuentro entre ambas historias, de hecho, el capítulo 500, antes del 1.001, es la historia que cuenta Rami Elhanan sobre la muerte de su hija Smadar, mientras que el capítulo 500, después del 1.001, es la historia que narra Bassam Aramin sobre la muerte de su hija Abir.

Más aún, el número de capítulos, 1.001, y su distribución simétrica también enlaza con la idea de apeirógono, infinitos lados (simbolizado por el 1.000) cerrándose y aproximándose al límite, 1.001, como el punto de acumulación que hemos explicado con anterioridad, en el apeirógono cerrado.

Sobre la estructura de las obras literarias escribe McCann lo siguiente en su artículo Buscando estructura, del libro 50 consejos para ser un buen escritor (puede leerse el artículo entero en la página web del escritor).

Una estructura adecuada refleja el contenido de la historia que quiere contar. Se siente apropiada. Respeta la historia. Contendrá a sus personajes y los impulsará hacia adelante al mismo tiempo. Y, por lo general, lo logrará más plenamente cuando no llame la atención sobre sí misma. La estructura debe surgir de los personajes y la trama, lo que esencialmente significa que surge del lenguaje. En otras palabras, la estructura está siempre en proceso de formación. La encuentras a medida que avanzas. Capítulo a capítulo. Voz a voz. Pregúntate si te parece adecuado contar la historia de una sola vez, o si debería dividirse en secciones, o si debería tener múltiples voces, o incluso múltiples estilos. Todas estas preguntas son importantes. Avanzas a tientas en la oscuridad, probando cosas nuevas todo el tiempo. A veces, de hecho, no encuentras la estructura hasta la mitad, o incluso cuando estás a punto de terminar. No pasa nada. Tienes que confiar en que al final aparecerá y que tendrá sentido. A menudo te sorprenderá lo matemático que resulta ser el trabajo de los grandes escritores. No te preocupes. Esta matemática es algo que se descubre.

Números amigos

Existen parejas de números, llamados números amigos (véase la entrada Los números enamorados), con una fuerte conexión entre ellos, como la pareja 220 y 284. Empecemos por el número 284, que se puede escribir como la multiplicación de los números primos 71 y 2 de la siguiente forma 284 = 71 x 2 x 2. Por lo tanto, los divisores propios del 284 son 1, 2, 4, 71 y 142, cuya suma es

1 + 2 + 4 + 71 + 142 = 220.

Si ahora consideramos el número que nos ha salido, 220, y buscamos sus divisores propios, como 220 = 11 x 5 x 2 x 2, entonces estos son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, y la suma de ellos es

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,

precisamente el primer número. Por este motivo, se dice que los números 220 y 284 son números amigos. Es decir, dos números son amigos si la suma de los divisores (propios) del primero es igual al segundo, y viceversa.

Esta pareja de números amigos (220, 284) ya era conocida por los pitagóricos, quienes les atribuían propiedades místicas y jugaron un papel importante en relación con la amistad y el amor, tanto en la magia, la brujería o la astrología, como en la realización de horóscopos, pócimas de amor, talismanes y amuletos. Incluso muchos grandes matemáticos la asociaron con la amistad perfecta.

Los números amigos 220 y 284 tienen un valor simbólico en esta novela, ya que uno de los pilares de la misma es la amistad entre el palestino Bassam y el israelí Rami.

Pero también nos hablan de otra amistad, la primera persona israelí con la que establece una relación de amistad el palestino Bassam, cuando está en la cárcel, es el guardia Hertzl, que había estudiado matemáticas.

196

[…] La mayor parte de la condena la pasó en la celda de aislamiento. El ritual exigía rezar en una esterilla de oración limpia. Usaba una tela azul sobre la que dibujó un mihrab. El guardia, Hertzl, se arriesgó para dársela. Bassam la enrolló meticulosamente y la escondió sin llamar la atención.

Al principio se pelearon. Hertzl era alto, delgado, de cara afilada, y tenía una nuez prominente. Lo habían educado como judío ortodoxo y había estudiado Matemáticas en Tel Aviv. Le llamó la atención el hecho de que el número de preso de Bassam fuese 220-284. Algo que tenía que ver con lo que él llamaba “números amigos”.

Bassam intentó recordar una clase sobre Al-Khwarizmi y la Casa de la Sabiduría. No se acordaba del todo, pero le dijo a Hertzl que todas las matemáticas provenían de los árabes, que eso lo sabía todo el mundo. Empezaron a hablar. […]

Posteriormente, en el capítulo 220 (de la primera mitad de la novela) se explica que son los números amigos y que 220 y 284 son una pareja de números amigos, la única por debajo del número 1.000, mientras que el capítulo 284 (de la primera mitad) está formado por un cuadrado blanco, es decir, no hay nada ya que este número está reservado por su relación de amistad con el 220. Por otra parte, los capítulos 220 y 284 de la segunda mitad de la novela repiten el contendido de los de la primera mitad, resaltando la importancia de la amistad en esta historia.

Para terminar

La novela incluye más referencias matemáticas, además de las comentadas más arriba, como, por ejemplo, las tablas de multiplicar que estaba memorizando Abir para el examen que tenía al día siguiente de su asesinato.

39

En el siglo IX, el matemático persa Mohammad ibn Musa Al-Khwarizmi escribió El compendio sobre cálculo por resolución e imaginación.

Fue un libro que introdujo el concepto de álgebra entre los estudiantes europeos. Al-Khwarizmi desarrolló una teoría unificadora que permitía tratar los números racionales e irracionales como objetos algebraicos.

Se trataba de trasladar cantidades de un lado de la ecuación al otro para mantener equilibrios.

38

La palabra álegebra viene del árabe al yabr, y tiene que ver con la reparación de los huesos rotos.