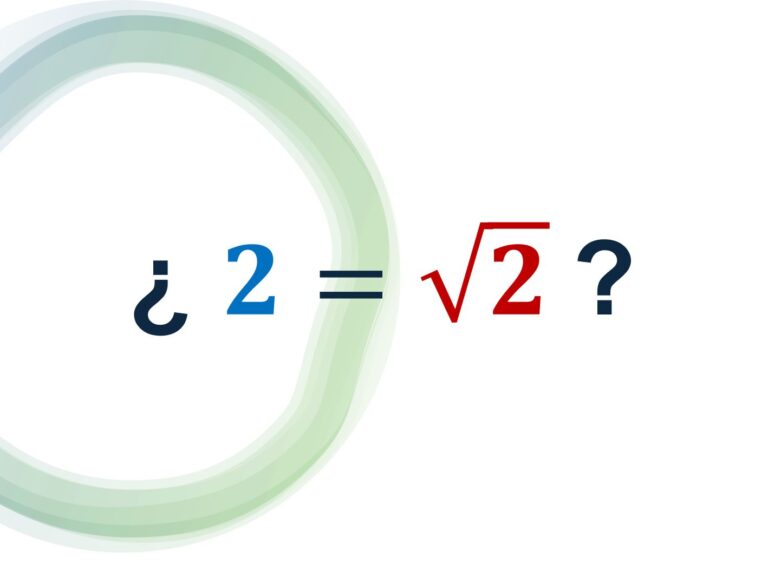¿Es 2 igual a raíz de 2?
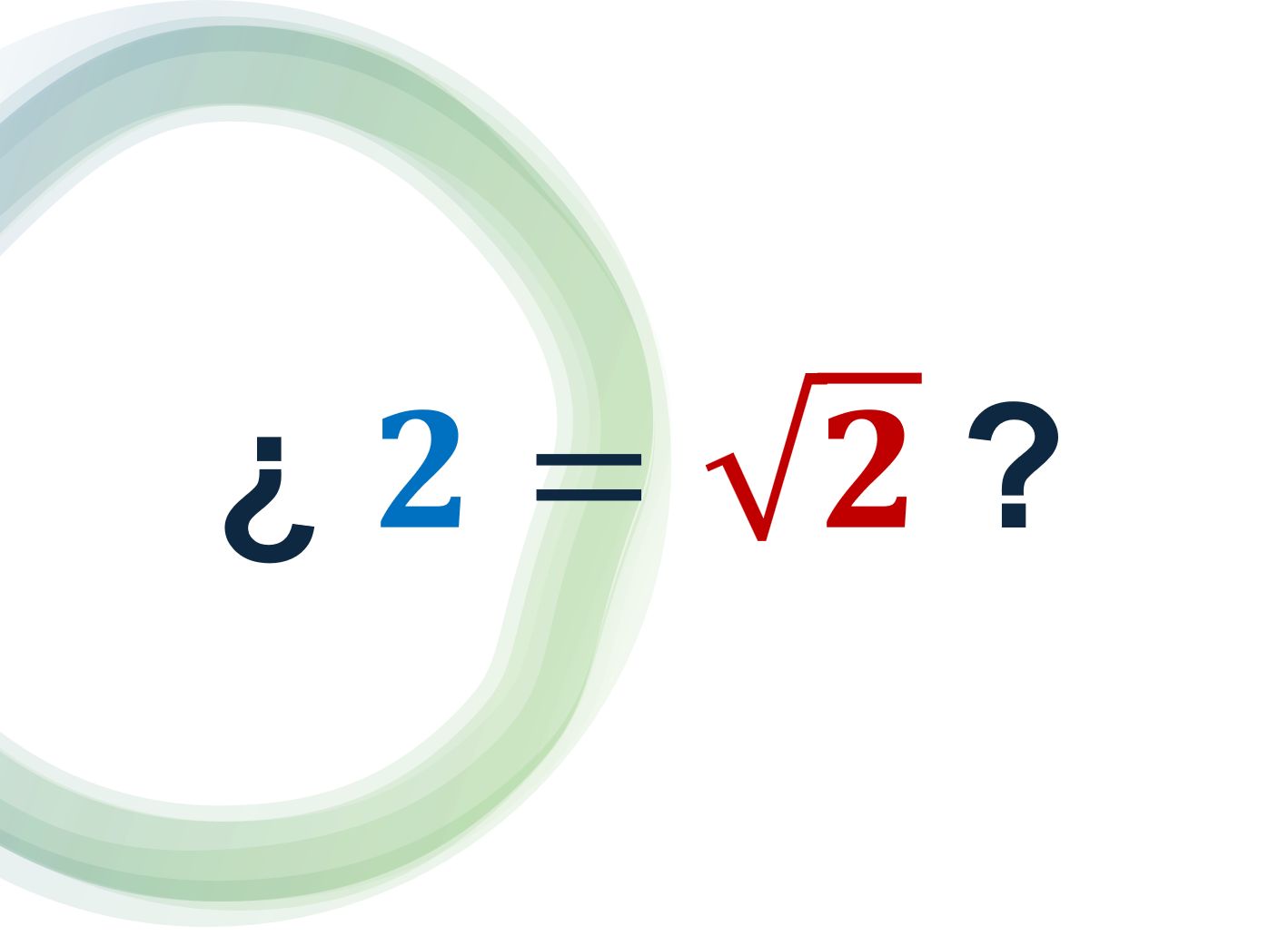
Una pregunta un tanto extraña, ¿no? Cualquiera sabe que la respuesta es negativa… ¿Seguro?
Una demostración de que 2 es igual a raíz de 2
Observa la imagen de debajo en la que se dan seis imágenes del cuadrado unidad [0,1] x [0,1] en el plano con ciertos subconjuntos marcados en rojo.
En la primera imagen, se marcan en rojo el intervalo vertical {0} x [0,1] y el horizontal [0,1] x {1}, cuya suma de longitudes es d = 1 + 1 = 2. Podemos pensar la unión de estos dos intervalos como un peldaño de una escalera de la que hemos medido la suma de su longitud y altura.
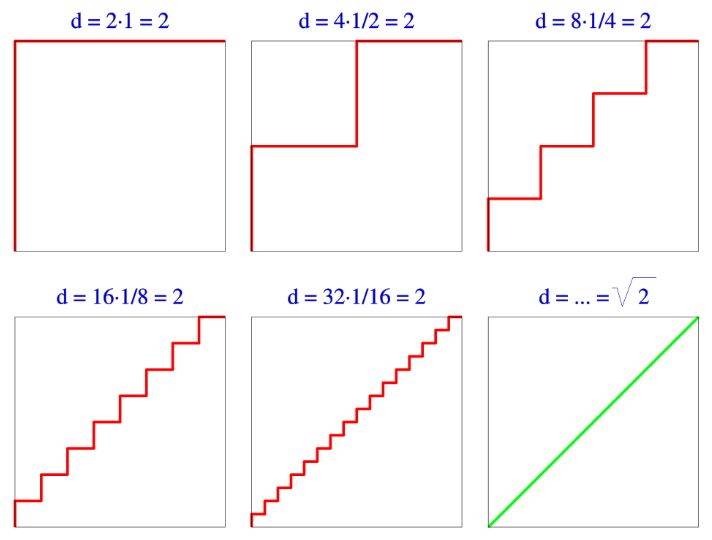
Vamos a ir construyendo sucesivamente escaleras uniendo los puntos (0,0) y (1,1), multiplicando en cada paso los peldaños por 2 y reduciendo la longitud y altura de cada peldaño a la mitad. Así, el segundo dibujo muestra, una escalera con dos peldaños, cada uno de los cuales posee una longitud y una altura de 1/2. Así, la suma de las longitudes y alturas de los peldaños de la escalera es d = 2 (1/2 + 1/2) = 2.
En el tercer dibujo se representa una escalera con 4 peldaños (siempre uniendo los puntos (0,0) y (1,1) del plano), cada uno de los cuales posee una longitud y una altura de 1/4. La suma de las longitudes y alturas de esos 4 peldaños es d = 4 (1/4 + 1/4) = 2.
En la cuarta imagen vemos una escalera de 8 peldaños, cada uno de los cuales tiene una longitud y una anchura de 1/8. Como en los casos anteriores, un simple cálculo muestra que la suma de las longitudes y alturas de esos 8 peldaños es d = 8 (1/8 + 1/8) = 2.
Continuando de este modo, en el paso n de este proceso tendríamos una escalera de 2n-1 peldaños, cada uno de los cuales tiene una anchura y una altura de 1/2n-1. La suma de las longitudes y alturas de esos 2n-1 peldaños es d = 2n-1 (1/2n-1 + 1/2n-1) = 2.
Podemos continuar indefinidamente este proceso en el que, para cualquier etapa de la construcción, la suma de la longitud y la anchura de todos los peldaños de esa escalera es de 2. En el límite, esa escalera se convierte en la diagonal del cuadrado, la línea recta que une los puntos (0,0) y (1,1), que mide raíz cuadrada de 2 por el teorema de Pitágoras. Así, queda demostrado que… ¡2 es igual a raíz de 2!
Algo debe de ser falso en este argumento…
La paradoja de la escalera
El anterior argumento lleva a la conocida como paradoja de la escalera: hemos construido una sucesión de escaleras en el cuadrado unidad, formadas por peldaños de longitud y altura decreciente. Estas escaleras convergen uniformemente a la diagonal del cuadrado, pero de manera que la suma de longitudes de los tramos de escalera (pensemos esta cantidad como la longitud de la escalera) no converge a la longitud de la diagonal.
Esta paradoja demuestra que los límites de las curvas no preservan necesariamente la longitud del arco. La longitud del arco se conserva bajo límites uniformes solo si las derivadas también convergen uniformemente. En este caso, la dirección de cada escalera es siempre horizontal o vertical, y no se acerca en ningún momento al ángulo de 45 grados de la diagonal.
¿Y si usamos la distancia de Manhattan?
Recordemos que la distancia de Manhattan entre dos puntos del plano a=(a1,a2) y b=(b1,b2) se define como |a1-b1|+|a2-b2|, es decir, es la suma de la distancia entre las primeras coordenadas de los puntos (horizontal) y la distancia entre las segundas coordenadas (vertical).
Así, en el cuadrado unidad, la distancia de Manhattan entre los puntos (0,0) y (1,1) es precisamente 2. En este caso, no habría paradoja: las escaleras construidas mediante el procedimiento descrito al principio son tan solo recorridos alternativos para viajar del punto (0,0) al punto (1,1), moviéndonos exclusivamente horizontal o verticalmente. Esas escaleras convergen en forma y en longitud a “la diagonal” (medida con la distancia de Manhattan) del cuadrado.
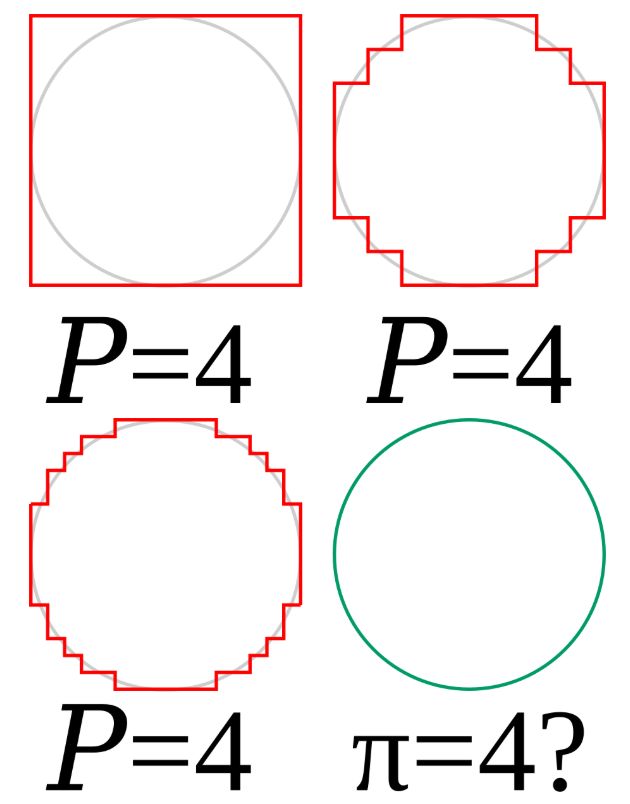
Y el número pi, ¿es igual a 4?
¡No! ¡Y tampoco es igual a 3,2 (gracias al matemático Clarence Abiathar Waldo, por cierto)! Pero la paradoja de la escalera podría llevarnos a demostrar que pi es 4…
La linterna de Schwarz
La paradoja denominada linterna Schwarz presenta el mismo problema que la paradoja de la escalera, pero en dimensión tres. La linterna de Schwarz es una aproximación poliédrica (formada por anillos apilados de triángulos isósceles. situados dentro de cada anillo siguiendo el mismo patrón que un antiprisma) a un cilindro que demuestra que no siempre es posible definir el área de una superficie como el límite de las áreas de los poliedros que convergen a ella. Puede verse la construcción precisa en este enlace.
¡Y mucho cuidado con los argumentos engañosos!
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la EHU y editora de Mujeres con Ciencia