El brillante matemático húngaro Paul Erdös (1913-1996) solía hablar de EL LIBRO en el que Dios había escrito las demostraciones más bellas de entre todos los teoremas. En una conferencia celebrada en 1985 Erdös dijo una de esas frases que se ha quedado para el recuerdo “No tenéis porque creer en Dios, pero deberíais creer en EL LIBRO”.

En 1998 los matemáticos Martin Aigner y Günter M. Ziegler publicaron El libro de las demostraciones (en castellano se publicó en Nivola en 2005) con el objetivo de incluir algunas de esas bellas demostraciones de las que hablaba Paul Erdös. Contiene teoremas, con sus correspondientes demostraciones, en algunos casos varias demostraciones de un mismo resultado, de Teoría de Números, Geometría, Análisis, Combinatoria y Teoría de Grafos.

En la sección Matemoción del Cuaderno de Cultura Científica ya incluimos hace un tiempo una de esas elegantes demostraciones que pertenecen a El Libro de las demostraciones, una hermosa prueba del conocido como Teorema de la galería de arte.

En esta entrada vamos a mostrar una hermosa demostración de la conocida fórmula de Cayley para árboles etiquetados, luego perteneciente a la Teoría de grafos. En mi anterior entrada La ratonera, un juego de Cayley ya mencioné brevemente al matemático inglés Arthur Cayley (1821-1895), autor del resultado que nos interesa en esta entrada.

Para empezar vayamos con los conceptos matemáticos básicos de Teoría de grafos.

• Grafo. Un grafo está formado por un conjunto de puntos, llamados vértices, y un conjunto de aristas, cada una de las cuales une dos vértices. Salvo que se diga lo contrario un grafo tiene un número finito de vértices y aristas.
• Grado de un vértice. Se llama grado de un vértice al número de aristas que inciden en el mismo.
• Camino. Un camino es una sucesión de vértices y aristas, que se inicia en un vértice y se termina en otro.
• Camino simple, ciclo. Un camino en el que no se repite ningún vértice se llama camino simple, y si es cerrado, se dice que es un ciclo.
• Grafo conexo. Un grafo en el que cada par de vértices está conectado, al menos, por un camino simple, se dice que es conexo.
• Árbol. Un grafo en el que cualesquiera dos vértices están conectados exactamente por un camino, es un árbol. Equivalentemente, es un grafo conexo que no posee ciclos.
• Grafo o árbol etiquetado. Un grafo, en particular también un árbol, al que asignamos etiquetas a sus vértices (o también a sus aristas) es un grafo etiquetado. Las etiquetas pueden ser números, letras u otros símbolos.

Antes de entrar en la enumeración de los grafos etiquetados veamos un par de resultados sencillos sobre árboles, que hay que tener en cuenta.

Teorema 1: Todo árbol, con al menos dos vértices, tiene un vértice de grado 1.

Se puede dar una sencilla prueba de este hecho (quien lo desee puede saltarse la lectura de la misma). Sea v₁ un vértice cualquiera del árbol, si tiene grado 1 se satisface el resultado, sino tendrá grado ≥ 2. En este caso, existen dos vértices v₀ y v₂ conectados, mediante sendas aristas, a v_1. Considérese ahora v₂, si tiene grado 1 se concluye el resultado, sino tendrá grado ≥ 2 y existirá un nuevo vértice v₃ conectado con v₂, que no puede ser ni v₀, ni v₁ (conectado con doble arista con v₂), ya que un árbol no tiene ciclos.

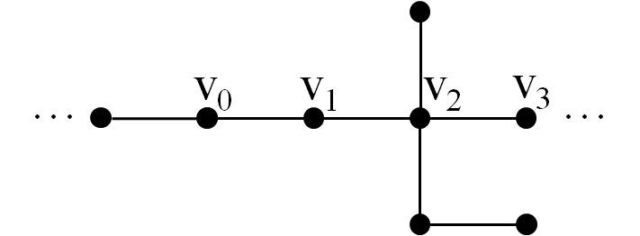
Y los mismo con v₃, si tiene grado 1 se concluye, sino tiene grado ≥ 2 y existe un nuevo vértice v₄, que no puede ser ninguno de los anteriores, para que no existan ciclos. De esta forma se genera una sucesión infinita de vértices conectados, pero los árboles que estamos estudiando tienen un número finito de vértices, luego necesariamente habrá un vértice con grado 1.

Teorema 2: Todo árbol con n vértices, tiene n – 1 aristas.

Se puede realizar una sencilla prueba por inducción de este resultado, que no realizaremos aquí, pero podéis comprobarlo a través de algunos ejemplos, como el mostrado arriba.

Centrémonos ahora en los árboles etiquetados, los cuales aparecen en muchas aplicaciones en problemas reales, por ejemplo, en cuestiones de minería de datos, computación o análisis de estrategias (por ejemplo, en los juegos), por mencionar alguno.

Aunque en esta entrada no estamos interesados en sus aplicaciones, sino en una de las bellas demostraciones que existen de la fórmula de Cayley, expresión matemática que permite calcular cuántos árboles etiquetados existen. Para tener una idea de cuál puede ser esa fórmula matemática, analicemos primero cuántos árboles etiquetados hay con 1, 2, 3 ó 4 vértices. Es fácil comprobar que existe un único árbol con 1 ó 2 vértices y tres con 4 vértices, como se muestra en la imagen.

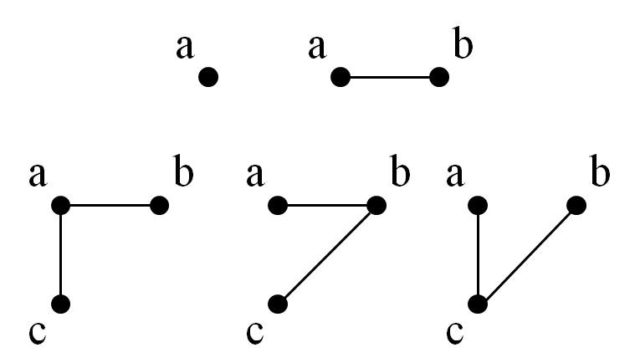
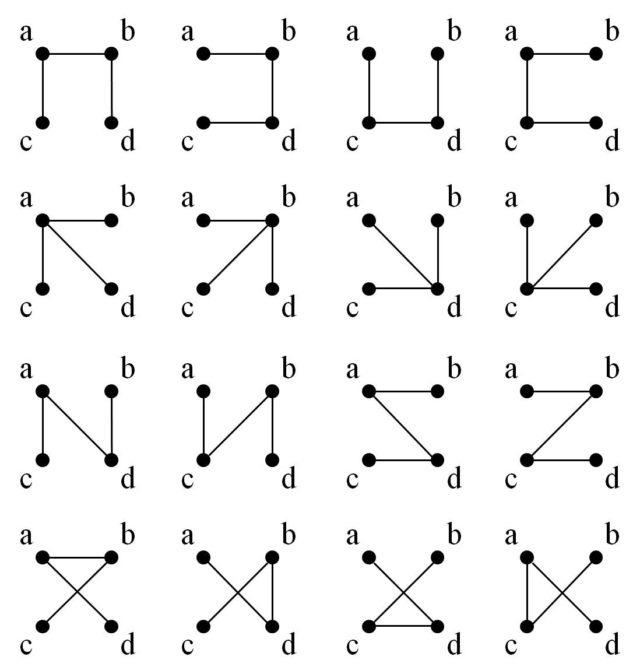
Con 4 vértices ya hay más árboles etiquetados, exactamente 16.

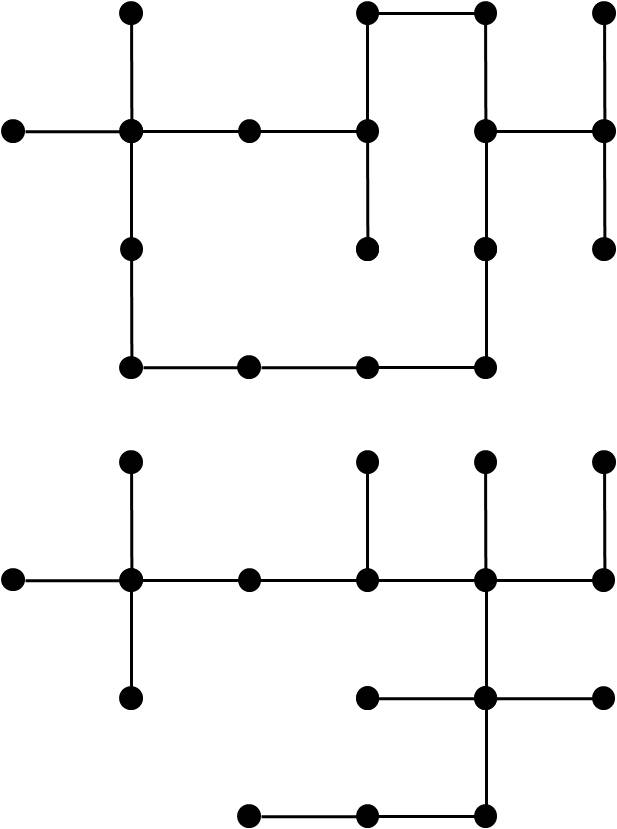
Para 5 vértices ya hay 125 árboles etiquetados. Para verlo, tomemos los tres árboles distintos con 5 vértices que existen (árboles no etiquetados), como se muestra en la siguiente imagen.

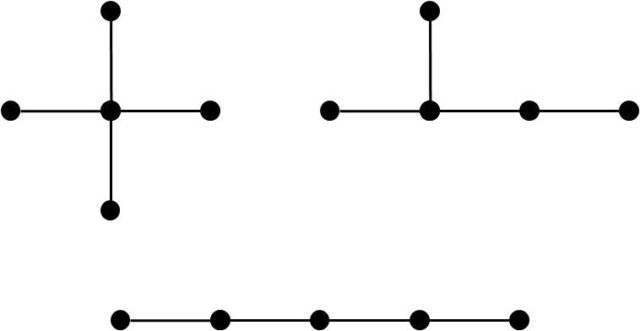
Y ahora veamos de cuántas formas distintas se pueden etiquetar esos tres árboles con 5 etiquetas (por ejemplo, las letras a, b, c, d, e).

Del primer árbol se obtienen 5 árboles etiquetados, que quedan determinados por la letra del vértice del centro, luego 5 posibilidades. De forma similar, se puede demostrar que para cada uno de los otros dos árboles hay 5 x 4 x 3 = 60 árboles etiquetados. Luego, en total, 125.

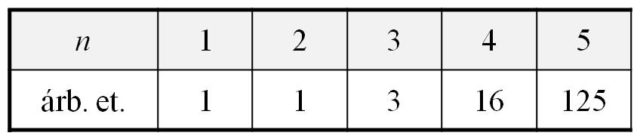
Dados esos primeros valores podríamos especular con una fórmula que nos diera el número de árboles etiquetados con n vértices, por ejemplo, n^{n – 2}. Esa es exactamente la fórmula que obtuvo Arthur Cayley en su artículo Un teorema sobre árboles (Quarterly Journal of Pure and Applied Mathematics, 1889).

Teorema (fórmula de Cayley): Para todo número entero n ≥ 2, existen n^{n – 2} árboles etiquetados distintos con n vértices.

En El libro de las demostraciones existen varias pruebas de la fórmula de Cayley, una de ellas utiliza las matrices y los determinantes, y en otra se realiza un razonamiento por recursión.

La demostración que vamos a mostrar en esta entrada, sencilla y hermosa al mismo tiempo, se debe al matemático Heinz Prüfer (1896-1934), que la publicó en la revista Archiv der Mathematik und Physik, en 1918. Consiste en asignar a cada árbol etiquetado, de n vértices, un código numérico de n – 2 elementos (llamado código, o secuencia, de Prüfer).

Veamos la demostración de Prüfer, según se muestra en el libro How to count, An introduction to combinatorics:

La fórmula es trivial para un árbol con dos vértices, n = 2, solo existe un árbol etiquetado posible. Luego se va a suponer que el árbol tiene n ≥ 3 vértices. Además, se supone que el árbol está etiquetado con los números naturales {1, 2, …, n}.

¿Cómo asignar un código numérico (a₁, a₂, …, a_{n – 2}) al árbol etiquetado? Primero se muestra el método general y después un ejemplo particular, que ayude a entender el procedimiento.

Empecemos considerando los vértices de grado 1 del árbol, que como hemos visto en el teorema 1 siempre existen, y tomemos el vértice v con el número de etiqueta más pequeño. Ahora, consideremos el único vértice w que está unido a v, puesto que su grado es 1, y llamemos a₁ a la etiqueta de w.

Entonces, se elimina el vértice v y la arista vw, que une v y w, quedando un nuevo grafo, que sigue siendo un árbol. Y se repite el proceso anterior con este nuevo árbol, se elige el vértice v’ de grado 1 con número de etiqueta más pequeño, el vértice w’ conectado, mediante una arista, con el mismo y se llama a₂ a la etiqueta de w’. Y entonces, se elimina el vértice v’ y la arista v’w’, obteniéndose un nuevo árbol sobre el que se repite el razonamiento. Este proceso se repite hasta que solo quedan dos vértices. El resultado es una secuencia (a₁, a₂, …, a_{n – 2}), el código de Prüfer del árbol etiquetado.

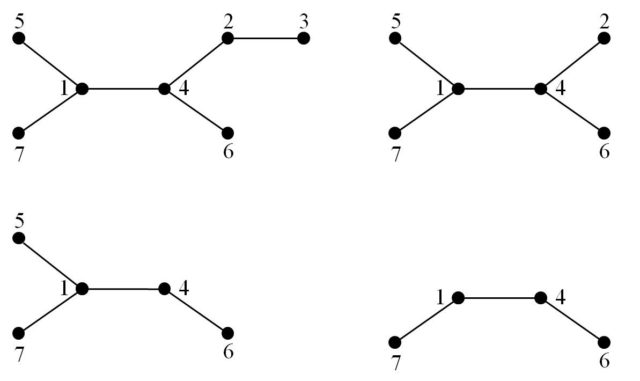
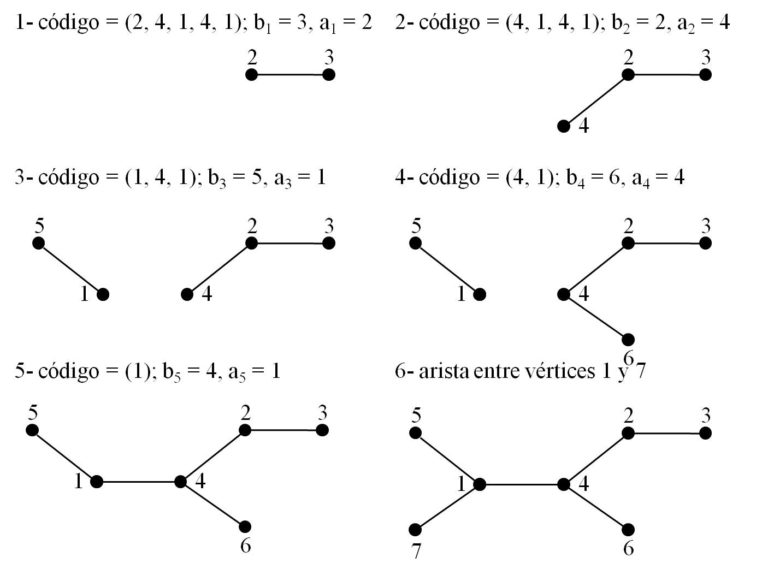
Veamos un ejemplo concreto. Se considera el árbol etiquetado, con 7 vértices, de la imagen anterior. Hay 4 vértices de grado 1, etiquetados con los números 5, 7, 3, 6, y el más pequeño, que es el que consideramos como v, es el vértice etiquetado como 3. Este está conectado a 2, luego a₁ = 2. Entonces se eliminan el vértice 3 y la arista (23), como en la imagen.

En el árbol resultante hay de nuevo 4 vértices de grado 1, siendo el de menor etiqueta el vértice 2, que está unido al vértice 4, luego a₂ = 4. Se elimina el vértice 2 y la arista (24), quedando el árbol que aparece en la imagen. Ahora hay tres vértices de grado 1, de los cuales el de menor etiqueta es el 5, que está unido al vértice 1, entonces, a₃ = 1. Continuando de esta forma se obtienen los valores a₄ = 4 y a₅ = 1, luego el código asociado a este árbol de 7 vértices es (2, 4, 1, 4, 1).

Pero también debemos ver el camino inverso, es decir, dado un código de Prüfer (a₁, a₂, …, a_{n – 2}), determinar el único árbol etiquetado asociado al mismo.

El árbol etiquetado va a tener n vértices y las etiquetas serán {1, 2, 3, …, n}. Se empieza considerando el número b₁, de entre los que van a ser etiquetas, que es el más pequeño de los que no están en (a₁, a₂, …, a_{n – 2}). Entonces se considera un vértice con la etiqueta b₁ y se une al vértice con etiqueta a₁. A continuación, se considera el número más pequeño b₂, distinto de b₁, que no está en la secuencia (a₂, …, a_{n – 2}) y se une el vértice b₂ con el vértice a₂. Después se toma el menor número b₃, distinto de b₁ y b₂, que no está en (a₃, …, a_{n – 2}) y se une el vértice b₃ con el vértice a₃. Y se continúa el proceso hasta obtener b₁, b₂, …, b_{n – 2} , y entonces se unen los dos vértices con etiquetas que no están entre esos n – 2 números.

A modo de ejemplo, veamos el proceso inverso al visto en el anterior ejemplo. Es decir, empezamos con el código (2, 4, 1, 4, 1) y veamos cómo obtener el árbol etiquetado asociado. En la imagen se va indicando en cada paso del proceso quienes son las etiquetas b_k que van apareciendo y los vértices que se van uniendo mediante una nueva arista (a_k b_k).

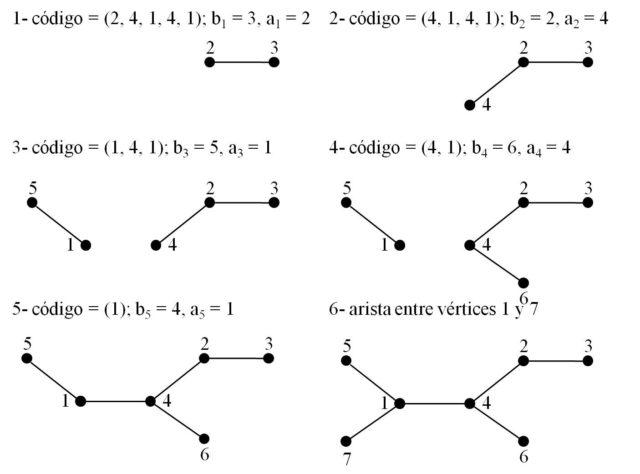
En conclusión, hemos probado que existe una correspondencia uno a uno entre los árboles etiquetados con n vértices y las secuencias de números (a₁, a₂, …, a_{n – 2}), donde los elementos de la secuencia a_k son números del conjunto de posibles etiquetas {1, 2, …, n}. Por lo tanto, como el número de posibles códigos de n – 2 números que pertenecen al conjunto {1, 2, …, n} es n^{n – 2}, se concluye que este es el número de árboles etiquetados distintos con n vértices.

La fórmula de Cayley fue publicada por primera vez en 1860 por el matemático alemán Carl Wilhelm Borchardt (1817-1880), quien la demostró utilizando determinantes. El resultado de Borchardt no estaba planteado realmente sobre árboles etiquetados y fue Cayley quien lo planteó en el contexto de la teoría de grafos.

Bibliografía

1.- Martin Aigner, Günter M. Ziegler, El libro de las demostraciones, Nivola, 2005.

2.- Raúl Ibáñez, Arthur Cayley, explorador victoriano del territorio matemático, RBA, 2017 (pendiente de publicación).

3.- Arthur Cayley, The Collected Mathematical Papers, Internet Archive [archive.org].

4.- Arthur Cayley, A theorem on trees, Quarterly Journal of Pure and Applied Mathematics, 23 (1889), p. 376-378.

5.- Heinz Prüfer, Neuer beweis eines satzes über permutationen (A new Prof. of a theorem on permutations), Archiv der Mathematik und Physik (3), 27 (1918), p. 142-144.

6.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.

7. C. W. Borchardt, Über eine Interpolationsformel für eine Art Symmetrischer Functionen und über Deren Anwendung, Math. Abh. der Akademie der Wissenschaften zu Berlin (1860), p. 1–20.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica