Mah-nà mah-nà

Hay tonadillas tan conocidas que es imposible empezar escucharlas sin esperar ansiosamente su continuación.

Tu tu rururu.

Pero lo curioso de las expectativas musicales es que operan aunque sea la primera vez que escuchamos una determinada canción. En ese caso, las expectativas se basan en todo lo que sabemos (sin saberlo) de la música gracias a haber escuchado muchas otras canciones antes. De nuevo: con cada escucha hemos ido construyendo un modelo, un sentido de lo que es musical, que aplicamos a cada nueva escucha intentando siempre adivinar cuál es la nota que vendrá. Y, por supuesto, no manejamos un único modelo. Existen expectativas armónicas, rítmicas, tímbricas… que pueden ser generales o ajustarse a un determinado estilo musical.

Pero, por ahora, ciñámonos a las expectativas melódicas. En el post anterior comentamos algunas de los métodos que utiliza la psicología para medirlas. Ahora cabe preguntarse: ¿cuáles son esas expectativas?, ¿son verdaderamente descriptivas?, es decir: ¿se ajustan realmente a las melodías que solemos escuchar?

La buena noticia es que tenemos un montón de datos para averiguarlo. Basta tomar unas cuantas partituras (o unos cuantos miles) y empezar a buscar patrones. Estas son algunas de las cosas que la estadística nos cuenta sobre las melodías.

Grados conjuntos.

Piensa en tu canción preferida; en la primera estrofa, específicamente. No necesito ser adivina para saber que el cantante entona varias sílabas sobre la misma nota. Tiene truco, pensarás: la estrofa suele ser la parte menos lucida de la canción, la más monótona desde el punto de vista melódico. Pero incluso si jugamos con el estribillo, lo más probable es que todos los intervalos melódicos sean muy pequeños (de un tono normalmente) y que haya sólo un par de saltos, si acaso, un poco mayores.

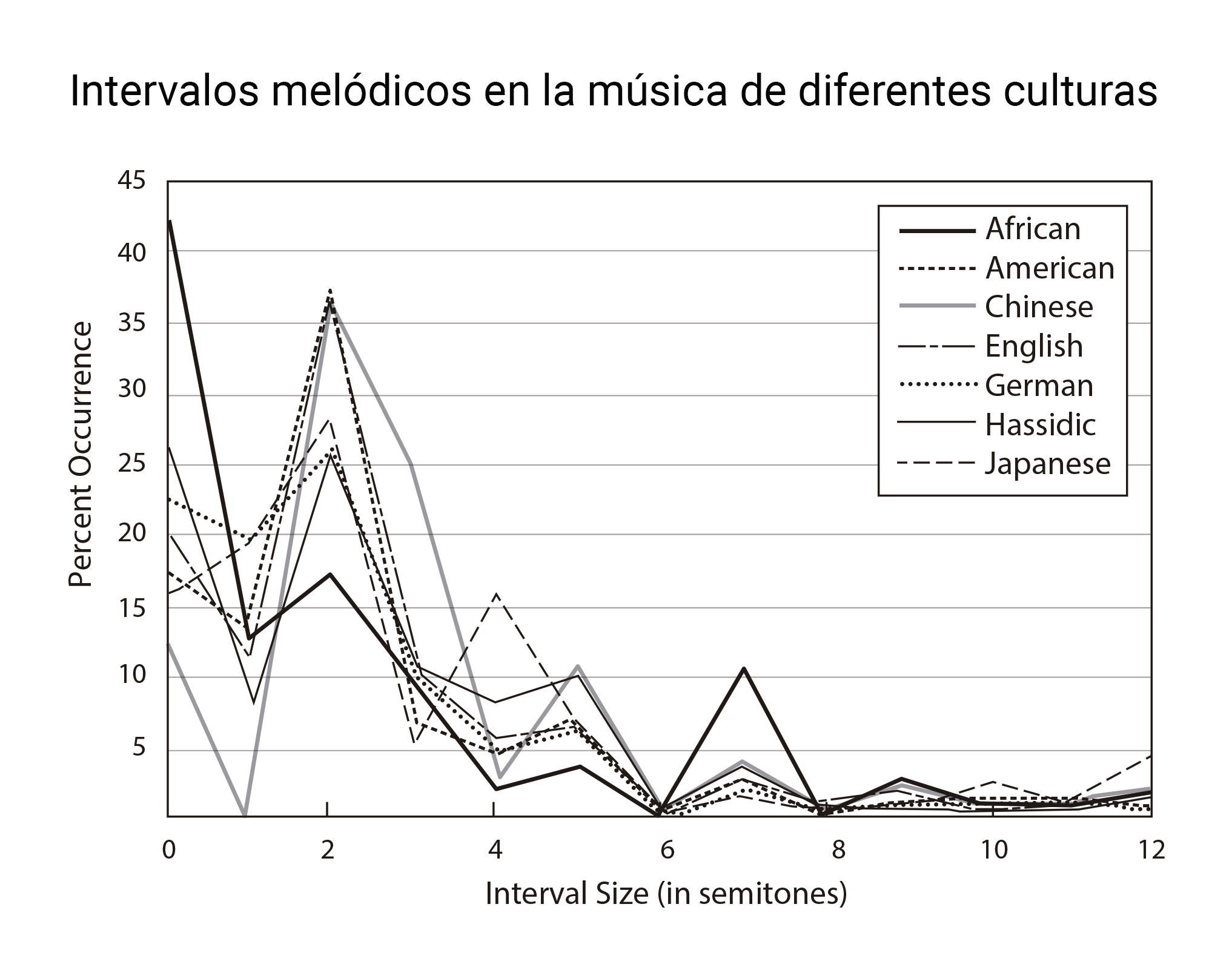
No es magia: es estadística. Las melodías más comunes se construyen, principalmente, por grados conjuntos. Y no se trata de un rasgo exclusivo de nuestra cultura. Podéis observarlo en la gráfica anterior¹: a lo largo y ancho del planeta, los intervalos pequeños tienden a predominar, quizás debido a la dificultad que entraña cantar con precisión intervalos más amplios². Asimismo, en 1978, Diana Deutsch mostró que las expectativas de los oyentes reflejan este patrón general³. Existen, eso sí, llamativas excepciones, como los yoiks escandinavos o el canto tirolés.

Pasos descendentes:

Las melodías más comunes tienden a utilizar intervalos pequeños pero todavía podemos decir más: en caso de producirse algún salto, lo más probable es que este sea ascendente (es decir: de sonidos graves hacia sonidos más agudos). David Huron comprobó que esta es, también, una característica a nivel universal de la música con muy contadas excepciones: las melodías saltan hacia el agudo y descienden por pequeños pasos hacia sonidos más graves.

Lo interesante es que este mismo dibujo es común al habla. Desde el punto de vista de la entonación, cada vez que hablamos tendemos a elevar la frecuencia de nuestra voz muy rápidamente al principio de cada frase y después vamos descenciendo poco a poco hacia sonidos más graves. De nuevo, existen excepciones: la entonación de las preguntas, ascendente al final, es una de ellas. Pero, en general, podemos decir que la voz hablada tiende a descender lentamente; probablemente debido a que la presión ejercida por el aire procedente de los pulmones disminuye a medida que este se agota. En realidad, cantar requiere un control mayor del flujo de aire, por lo que no parece probable que las líneas descendentes de las melodías se deban a esta misma causa fisiológica. Más bien: parece ser un préstamo directo procedente de la prosodia del lenguaje.

Inercia:

Los pasos descendentes tienden a ir seguidos por más pasos descendentes. No sucede así con los intervalos ascendentes que pueden cambiar de sentido con igual probabilidad. Sin embargo las expectativas de los oyentes, en este caso, no se corresponden perfectamente con la estadística: tendemos a esperar inercia en ambos sentidos. Quizás este modelo sea lo bastante descriptivo con un menor coste “computacional”, por así decirlo, pero el motivo no termina de estar claro.

Regresión melódica:

Imagina que vas por la calle y te cruzas con un tipo de dos metros. Lo más probable es que la siguiente persona que te cruces sea más baja. No es una relación causal, evidentemente; una persona alta no causa la aparición de personas más bajitas. Pero los valores extremos de una distribución normal son, simplemente, menos probables. Esto es lo que se conoce como regresión a la media.

Como las alturas humanas, los tonos de una melodía muestran una tendencia central: esto es, dentro de un espacio acotado de sonidos (la tesitura de la melodía), las notas más probables son aquellas que no son ni muy graves, ni muy agudas; sino que están situadas hacia el centro del rango sonoro. Por tanto, cada vez que alcanzamos una nota extrema, lo más probable es que la siguiente nota esté más cerca de la media.

Nuestras expectativas, nuevamente, reflejan este hecho musical. Aunque no de forma perfectamente fiel… en este caso, cada vez que se produce un salto melódico, los oyentes esperan que la siguiente nota se mueva en dirección contraria al salto. Y suelen acertar, puesto que los saltos melódicos tienden a acercar la melodía a los extremos de su tesitura. Como en el caso de la inercia, el modelo parece simplificar la realidad del fenómeno que quiere anticipar. Dado que, habitualmente, sus predicciones resultan ser correctas, es lo bastante bueno.

A fin de cuentas, ese es el único propósito de las expectativas; no se trata de alcanzar un conocimiento exacto de la música, basta con acertar. Y de hecho, lo consiguen: las melodías que escuchamos encajan con lo que esperamos de ellas, con aquello que nos resulta más musical. Y ahora cabe preguntarse: ¿qué fue antes, el huevo o la gallina?, ¿nuestras expectativas describen la música que nos rodea, o nos rodea música que se ajusta a nuestras expectativas?, ¿cuánto espacio queda para innovar?

Referencias:

David Huron (2008) Sweet anticipation: music and the psychology of expectation. The MIT Press.

Notas: