Es una obviedad decir que los matemáticos y matemáticas de todo el mundo también comemos pizza, pero no lo es tanto mencionar que en ocasiones somos capaces de relacionar las pizzas con las matemáticas, más allá de la simple referencia a las fracciones.
Una primera relación trivial es que como las pizzas son circulares y conocemos cuál es el área de un círculo –exactamente π r2, si el radio de la pizza es r–, aunque para esto no hace falta ser matemático, podemos saber cuánto dinero nos cuesta cada unidad de área, por ejemplo, cada cm2, de pizza, dependiendo de las características y precio de la misma. Y por lo tanto, es posible que nos animemos a discutir de sencillas cuestiones como si sale más rentable comprar una pizza grande o dos medianas.
Pero esta cuestión de matemática cotidiana no es el objetivo de esta anotación en el Cuaderno, sino que estamos interesados en una cuestión relacionada con el reparto de los trozos de una pizza entre dos comensales. Me explico.
Imaginemos dos personas que han pedido una pizza, por ejemplo, mediana. Cuando les entreguen la pizza, esta estará cortada en ocho trozos y en condiciones ideales, es decir, que los cuatro cortes pasen por el centro y estén igualmente espaciados, lo que significa que están formando un ángulo de 45º entre cada dos de ellos, estos serán completamente iguales (como en la imagen). En tal caso, será fácil repartir la pizza, cada comensal simplemente tendrá que coger cuatro trozos cualesquiera, puesto que cada trozo tiene la misma superficie que el resto.
Pero lo normal es que esos cortes realizados en la pizzería no sean tan perfectos. Supongamos que aún así siguen una cierta regularidad, que los cuatro cortes pasen por un punto común, aunque no sea el centro del círculo que forma la pizza, y que estén igualmente espaciados, es decir, formando un ángulo de 45º entre cada dos de los cortes consecutivos (un ejemplo de esta situación de muestra en la siguiente imagen).
La cuestión ahora es si es posible repartir la pizza, sin realizar más cortes, de forma que cada una de las dos personas reciba la misma cantidad de la misma. Mirando a la imagen de la pizza cortada de esta forma no da la impresión de que sea posible repartir los trozos de manera equitativa, sin embargo, el conocido como Teorema de la pizza nos dice que sí es posible y además cómo hacerlo.
Teorema de la pizza: Si una pizza es dividida en ocho trozos, obtenidos mediante cuatro cortes que pasan por un punto común y forman un ángulo de 45º entres ellos, entonces la suma de las áreas de los trozos alternos son iguales (grises y blancos en la imagen anterior).
Esta cuestión fue originalmente propuesta por el matemático L. J. Upton en Mathematics Magazine, problema 660, en 1967 [1], y resuelta por Michael Goldberg también en Mathematics Magazine [2]. Este resultado no es matemáticamente complicado, y puede ser entendido por cualquier estudiante de matemáticas.
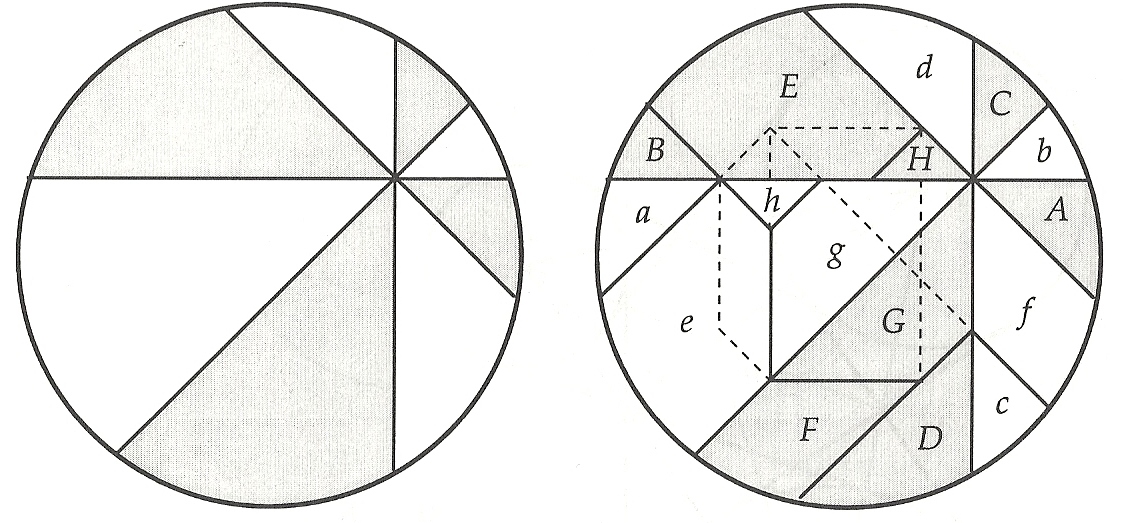
Larry Carter y Stan Wagon realizaron una demostración visual por medio de disecciones [3] que fue recogida en el libro Proofs without Words II, de Roger B. Nelsen [4] (véase la anotación Pitágoras sin palabras para un breve comentario sobre las demostraciones visuales y algún ejemplo), y que reproducimos aquí. Os dejamos que observéis el diagrama y comprobéis por vosotros mismos que efectivamente los trozos grises y blancos tienen la misma superficie total, viendo que los nuevos trozos más pequeños generados por Carter y Wagon mediante cortes de los anteriores se corresponden dos a dos en superficie.
El resultado del teorema de la pizza sigue siendo cierto para un número de cortes par mayor que 2, es decir, 4, 6, 8, etc., y por lo tanto, con un número de trozos de pizza mayor que 4 y múltiplo de 4, es decir, 8, 12, 16, etc. Una demostración mediante disecciones para el caso general ha sido dada por Greg Frederickson en 2012 [5].
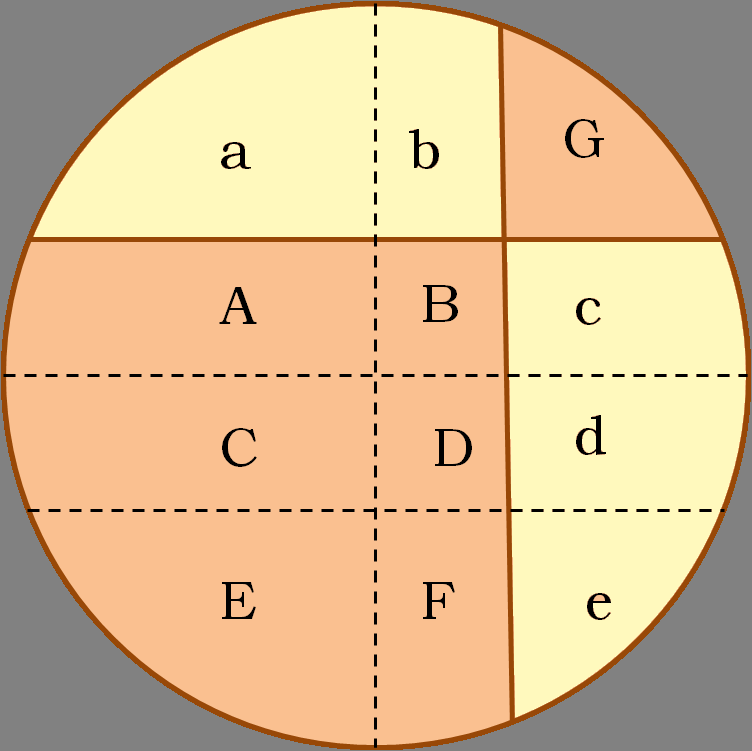
Sin embargo, para 2 cortes, o un número impar de cortes el resultado no es cierto. Para 2 cortes se comprueba con facilidad. Considérese por ejemplo el siguiente corte.
Entonces puede razonarse fácilmente que los trozos oscuros ocupan más superficie que los claros. Para ello trazamos dos rectas paralelas a los cortes y que pasen por el centro (diámetros), y una recta más, paralela a uno de los diámetros y que está a la misma distancia de este que el corte paralelo (véase imagen), y nombramos las zonas que se generan como aparece en la imagen (mayúsculas para la zona oscura y minúsculas para la clara). Claramente E = a, F = b y G = e, pero para el resto la zona oscura (A + B + C + D) es mayor que la clara (c+d).
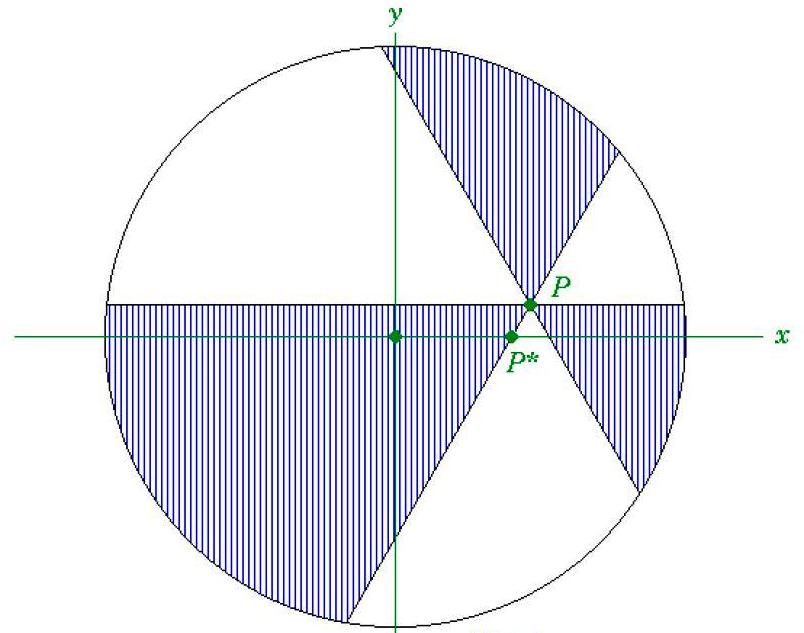
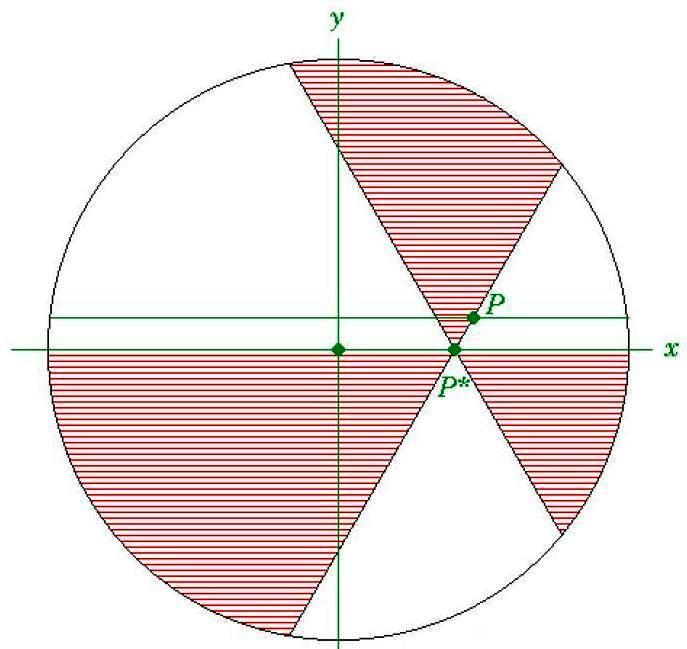
R. Mabry y P. Deiermann en 1995, dando respuesta al problema planteado por L. Carter, S. Wagon en Mathematics Magazine, problema1457, [6], demostraron que el resultado tampoco era cierto en el caso de un número impar de cortes [7]. El ejemplo que utilizaron fue el siguiente. Consideraron los siguientes tres cortes del tipo anterior sobre una pizza, es decir, que pasan por un punto común P y el ángulo entre cortes consecutivos es siempre el mismo, es decir, 60º, y demostraron que la superficie de los trozos azules es mayor que la de los blancos.
Para ello, trazaron los ejes coordenados x e y (o lo que es lo mismo, dos diámetros perpendiculares), consideraron el punto P* intersección del eje x con uno de los cortes, y trasladaron los cortes al punto P*. Y consideraron el nuevo corte, en el que, como se ve en el esquema siguiente, los dos grupos de trozos de pizza, rojos y blancos, tienen igual superficie en total.
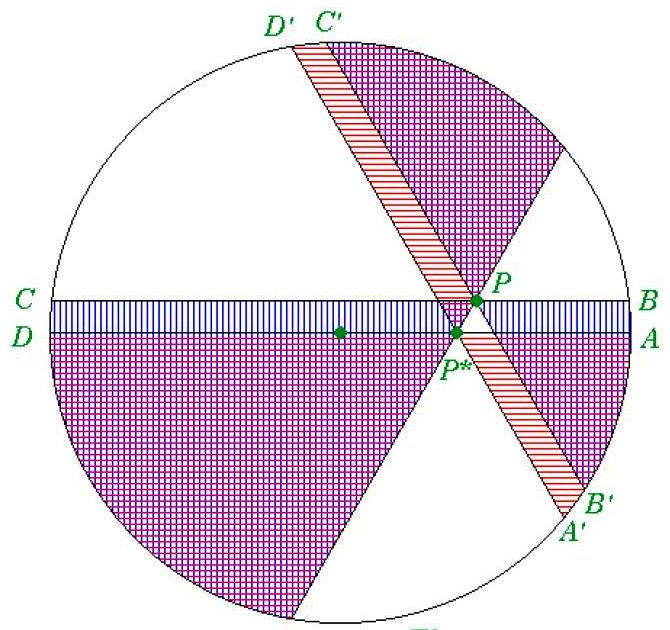
Finalmente consideraron los dos esquemas juntos. Entonces, como las zonas rojas y blancas (en el segundo esquema) tienen la misma superficie, y la banda ABCD menos un pequeño triángulo equilátero, que se corresponde con zona azul en el diagrama original, es mayor que la banda A’B’C’D’ menos un pequeño triángulo equilátero, que se corresponde con la zona blanca en el diagrama original, se concluye que en el esquema inicial la zona azul es tiene mayor superficie que la blanca.
La solución general al problema de la pizza fue dada por R. Mabry y P. Deiermann en 2009 y es la siguiente, que ellos nombran el teorema de la pizza de queso.
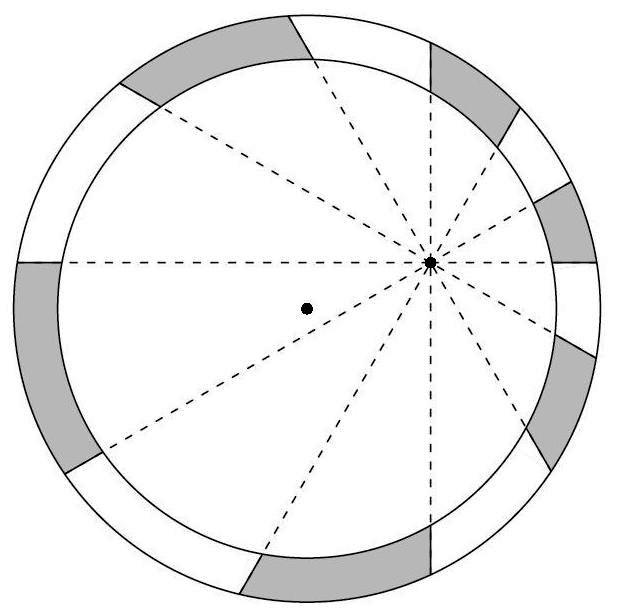
Teorema de la pizza de queso [8]: Si O es el centro de la pizza, esta se divide en n cortes a la “manera usual”, generando 2n trozos de pizza que se dividirán en dos familias de n trozos, grises y blancos, alternando uno de cada familia. Entonces,
i) si n > 2 es par o el centro O está en uno de los cortes, la superficie total de las zonas grises y de las zonas blancas es la misma,
ii) si O está en el interior de una zona gris y n≡3 (mod.4), es decir, n es de la forma 4r+3, entonces la superficie de las zonas grises es mayor que la de las blancas,
ii) si O está en el interior de una zona gris y n≡1 (mod.4), es decir, n es de la forma 4s+1, entonces la superficie de las zonas grises es menor que la de las blancas.
Pero Mabry y Deiermann demuestran algunos otros resultados relacionados con el teorema de la pizza de queso en su artículo [8], como por ejemplo, el teorema de la pizza de queso con borde grueso. Hay a personas a las que les gusta las pizzas con el borde grueso, y entonces nos podríamos plantear el problema de si se podría repartir los trozos de pizza de forma que también recibiese cada uno de los dos comensales la misma cantidad del borde grueso de la pizza.
El resultado demostrado por Mabry y Deiermann es el siguiente.
Teorema de la pizza de queso con borde grueso [8]: Sea un pizza de queso con un borde grueso (de una anchura constante) a la que le hacemos n cortes (mayor que 2) al estilo del teorema de la pizza de queso, con el punto de corte P en la zona del queso, y consideramos los trozos de pizza de nuevo de forma alternada (grises y blancos). Para n impar, los trozos de pizza que den más superficie de queso darán menos superficie de borde, y para n par, la cantidad de pizza y de borde será la misma en ambos repartos de trozos (grises y blancos).
Existen otras generalizaciones de estos estudios, por ejemplo, planteándose el reparto entre más de dos personas o cortando la pizza uniendo el punto P común con 8 puntos de la circunferencia exterior, igualmente espaciados, entre otras.
Pero el definitivo teorema de la pizza es el siguiente. Si consideramos que una pizza no es un círculo, sino un cilindro, entonces el volumen de la pizza, si tiene altura a y radio z, es igual a “pi z z a”.
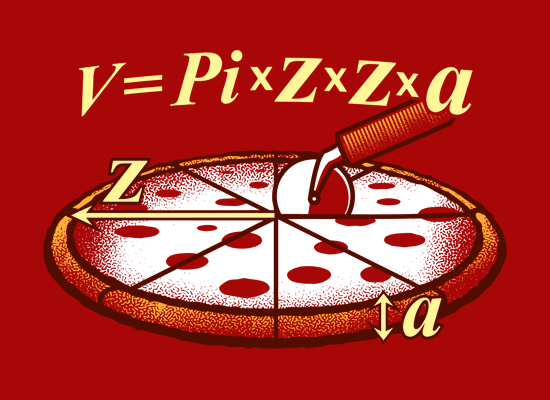
(Nota: recordar que el volumen de un cilindro de radio r y altura h es π r2h = π r r h = pi r r h)
Bibliografía:
1- L. J. Upton, Problem 660, Mathematics Magazine 40 (1967), p. 163.
2- L. J. Upton, Problem 660 (Solution by Michael Goldberg), Mathematics Magazine 41 (1968), p. 46.
3- L. Carter, S. Wagon, Proof without Words: Fair Allocation of a Pizza, Mathematics Magazine 67 (1994), p. 267.
4- R. B. Nelsen, Proofs without words II, MAA, 2000.
5- G. Frederickson, The Proof Is in the Pizza, Mathematics Magazine 85 (2012), p. 26–33.
6- L. Carter, S. Wagon, Problem 1457, Mathematics Magazine 67 (1994), p. 304.
7- R. Mabry, P. Deiermann, The center of a sliced pizza, Mathematics Magazine 68 (1995), p. 312-315.
8- R. Mabry, P. Deiermann, Of Cheese and Crust: A Proof of the Pizza Conjecture and Other Tasty Results, American Mathematical Monthly 116 (2009), p. 423–438 .
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
——————————————————–
Si te ha interesado esta anotación puedes ayudar a difundirla, votando aquí.




El teorema de la pizza
[…] El teorema de la pizza […]
El teorema de la pizza | Cuaderno de Cultura Científica
[…] El teorema de la pizza | Cuaderno de Cultura Científica […]
¡Póngame media docena de fibonaccis! | Matemoción | Cuaderno de Cultura Científica
[…] sin palabras en los artículos del Cuaderno de Cultura Científica, Pitágoras sin palabras, El teorema de la pizza, Regla de los números intermedios y el parque automovilístico de Bilbao o Formas ritmo-espacio) […]
Santiago
Vaya, que decepción! Creía que a nadie se le había ocurrido el problema de la pizza con 4 trozos (y no solo eso, sino mucho más, claro). Malditos sean nuestros antepasados, robaron todas nuestras ideas!
Muy interesante.
Se acerca el día PI | Profe, me he perdido…
[…] https://culturacientifica.com/2013/09/11/el-teorema-de-la-pizza/ […]
09.02 – El día de la Pizza – *días del año* | travelOgrafa
[…] Existe el teorema de la pizza. El cual dice que “si una pizza es dividida en ocho trozos, obtenidos mediante cuatro cortes que pasan por […]
La fórmula de la PIZZA | πlilismo
[…] Fuentes: https://culturacientifica.com/2013/09/11/el-teorema-de-la-pizza/ https://matesmates.wordpress.com/20…; […]