En noviembre de 2022, la artista donostiarra Esther Ferrer, la directora de Tabakalera, el Centro Internacional de Cultura Contemporánea de Donostia, Edurne Ormazabal, y el alcalde de Donostia/San Sebastián, Eneko Goia, presentaron ante la prensa una intervención artística para la futura plaza de acceso a Tabakalera. Como se pudo leer en diferentes medios de comunicación, se trata de una instalación que forma parte de su serie El poema de los números primos, realizada en cerámica de colores azul y verde, los que para la artista definen la ciudad de San Sebastián, junto con otros dos colores, el gris y el dorado. Este último es un homenaje a la matemática francesa Sophie Germain (1776-1831).

La matemática Sophie Germain

Nació en París, el 1 de abril de 1776, en una familia burguesa que participó en la revolución francesa. Durante la misma se refugió en su casa y dedicó su tiempo a la lectura de libros de la biblioteca. La impresionó mucho una historia de las matemáticas y la anécdota de la muerte de Arquímedes. Este gran matemático griego, que ya en su época alcanzó cierta fama, murió a manos de un legionario romano mientras se hallaba absorto en la resolución de un problema geométrico, durante el asalto de Siracusa (véase una explicación más extensa sobre su muerte en la entrada Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)). Estudió matemáticas por su cuenta, aunque con la oposición de su familia (por la noche le quitaban la luz, la calefacción y la ropa).

Como la Escuela Politécnica de París, que fue fundada en 1794, cuando Sophie tenía 18 años, no admitía a las mujeres como alumnas (de hecho, no las admitiría hasta 1972), ella consiguió hacerse con algunos apuntes, como los de Química del químico francés Antoine François, Conde de Fourcroy (1755-1809) o los de Análisis Matemático del matemático franco-italiano, Joseph-Louis Lagrange (1736-1818). Al final del periodo lectivo los estudiantes solían presentar sus investigaciones, o comentarios, a sus profesores, así que Sophie Germain envió un trabajo a Lagrange, firmándolo como Antoine-Auguste Leblanc, un antiguo alumno de la Escuela Politécnica. Este trabajo impresionó a Lagrange, quien quiso conocer al estudiante. Al averiguar su verdadera identidad la felicitó, la animó a seguir estudiando y predijo que tendría éxito como matemática. Ese encuentro la hizo famosa en la comunidad científica y empezó a relacionarse con científicos de la época. Alcanzó cierta notoriedad. Muchos le enviaban sus trabajos o se querían entrevistar con ella.

Cuando Sophie Germain empezó a escribir al gran matemático alemán Carl Friedrich Gauss (1777-1855) para compartir con él sus investigaciones en Teoría de Números (intentaba demostrar el Teorema de Fermat), firmó sus cartas con el seudónimo de “Monsieur Leblanc”. En 1906 con motivo de la campaña de Prusia de Napoleón, Sophie Germain temió que algo le ocurriera a Gauss y le escribió a un militar amigo suyo para que velara por la seguridad del matemático. El militar le escribió a Germain para comunicarle que Gauss estaba bien, que este le agradecía su mediación, pero que no conocía a ninguna Sophie Germain. Entonces la matemática francesa tuvo que escribirle para contarle que ella era Monsieur Leblanc. Gauss sorprendido al conocer su identidad, le escribió una carta alabando su talento, su valor y su genio, y comentando como una mujer encuentra más obstáculos que un hombre para trabajar en matemáticas debido a los prejuicios.

El resultado que lleva su nombre fue un avance muy importante en la demostración del Teorema de Fermat (que no se demostraría hasta 1995, por Andrew Wiles). Posteriormente se dedicaría al estudio de las superficies elásticas, intentando explicar matemáticamente los experimentos del físico alemán Ernst Florenz Friedrich Chladni (1756- 1827), los patrones geométricos que forma la música sobre las placas metálicas con arena, lo que le valdría el Premio de la Academia de Ciencias. Trabajó en otros temas como la curvatura o incluso en Filosofía de la Ciencia. Su ensayo filosófico Considérations générales sur l’état des Sciences y des Lettres aux différentes époques de leur culture / Consideraciones generales sobre las Ciencias y las Letras en las diferentes épocas de su cultura (1833), para identificar los procesos intelectuales de las “Ciencias” y las “Letras” e incluso de todas las actividades humanas, fue elogiado por el filósofo Augusto Comte.

Dedicó toda su vida a las matemáticas, no se casó nunca y murió de cáncer de mama en 1831. Poco antes de su muerte, en 1830, Gauss intentó que la Universidad de Gotinga, en Alemania, le otorgara el título de Doctor Honoris Causa, pero a pesar de su gran influencia en esta universidad, su propuesta fue rechazada.

El último teorema de Fermat

Como se comentaba más arriba el teorema que lleva asociado el nombre de esta matemática francesa, el teorema de Germain, que da lugar al concepto de número primo de Sophie Germain, está relacionado con el famoso último teorema de Fermat.

Empecemos recordando brevemente este importante resultado de la Teoría de Números (para más información sobre el mismo se puede leer la entrada Euler y el último teorema de Fermat o el artículo Avatares literarios del último teorema de Fermat).

El jurista francés y aficionado a las matemáticas Pierre de Fermat (1601-1665), inspirado en el problema de expresar el cuadrado de un número como la suma de los cuadrados de dos números, es decir, buscar soluciones de números enteros positivos a la ecuación pitagórica x² + y² = z² (existen infinitas soluciones, ternas pitagóricas, como (3,4,5) o (5,12,13)), problema que aparecía en el libro Aritmética del matemático griego Diofanto (alrededor del siglo III o siglo IV), se planteó extender ese problema a cualquier potencia y afirmó tener una demostración (el famoso margen en su ejemplar del libro de Diofanto), del hecho de que no existían soluciones para cualquier potencia, diferente de 2. Sin embargo, esa demostración nunca apareció y fue el inicio de una gran aventura matemática, la búsqueda de una demostración del llamado último teorema de Fermat.

Último teorema de Fermat: No es posible encontrar tres números enteros positivos x, y, z tales que verifiquen la ecuación, xⁿ + yⁿ = zⁿ, para n mayor, o igual, que 3.

El primer avance significativo en los intentos por demostrar el teorema de Fermat, en más de un siglo, se produjo de la mano del matemático suizo Leonhard Euler (1707-1783). Este estaba estudiando los papeles de Pierre de Fermat cuando en mitad de una demostración encontró un razonamiento válido para el teorema de Fermat cuando n = 4, es decir, de que no existen números enteros positivos x, y, z tales que x⁴ + y⁴ = z⁴. La técnica que utilizaba Fermat era la conocida con el nombre de “descenso infinito”.

Euler hizo uso de la técnica del descenso infinito, pero utilizando números complejos en el razonamiento, para demostrar la conjetura de Fermat para el caso n = 3, x³ + y³ = z³. Aunque Euler cometió un error en dicha demostración, el resultado necesario para corregirlo estaba en otro de los trabajos del matemático suizo, por lo que se sigue considerando válida su demostración. Las ideas de la demostración de Euler fueron generalizadas por matemáticos como el alemán Peter Gustav Lejeune Dirichlet (1805-1859), el francés Adrien-Marie Legendre (1752-1833) o el francés Gabriel Lamé (1795-1870) para probar algunos otros casos particulares, como, por ejemplo, n = 5 y 7.

Después del trabajo de Euler quedó claro que bastaba demostrar el último teorema de Fermat para los números primos impares. El argumento es el siguiente. Si un número primo p divide a n, entonces tendremos que n será el producto del número primo p con otro número q, es decir, n = pq. Por lo tanto, la ecuación xⁿ + yⁿ = zⁿ, puede escribirse como

de donde se deduce, que si la ecuación x^p + y^p = z^p, no tiene solución, tampoco la tendrá la anterior. Por otra parte, si ningún número primo impar divide a n, entonces n será una potencia de 2 y entonces 4 divide a n (para n = 2, ya sabemos la solución, son los triples pitagóricos). Por el mismo argumento anterior, si 4 divide a n, basta demostrar que la ecuación x⁴ + y⁴ = z⁴ no tiene solución, como ya sabemos, por el propio Fermat (a través de Euler, claro).

En consecuencia, había que intentar demostrar el último teorema de Fermat para los números primos impares. Pero solo se conocía la demostración para los primeros números primos impares, 3, 5 y 7. Y precisamente el primer resultado general vino de la mano de la matemática francesa Sophie Germain.

Los primos de Sophie Germain

El estudio de la ecuación x^p + y^p = z^p, para p un número primo impar, se dividió en dos casos. El primer caso cuando p no divide a x, y y z (es decir, que x, y y z no son múltiplos de p) y el segundo caso cuando p sí divide a alguno de los tres, x, y o z. El resultado de Germain se refería al estudio del primer caso del último teorema de Fermat y es el siguiente.

Teorema de Germain: Si p es un número primo, tal que 2p + 1 también es primo, entonces no existen números enteros x, y, z, no nulos y no múltiplos de p, tales que x^p + y^p = z^p.

Este resultado de Germain fue el primer resultado general en la demostración del último teorema de Fermat, que establecía una familia de números primos para los cuales no se cumplía el primer caso del último teorema de Fermat.

Debido al resultado anterior, a los números primos p tales que 2p + 1 es también primo se les llama primos de Sophie Germain (o primos de Germain). Por ejemplo, los números 2, 3 o 5 son primos de Sophie Germain, ya que 2 x 2 + 1 = 5, 2 x 3 + 1 = 7 y 2 x 5 + 1 = 11 son también primos. La sucesión de números primos de Sophie Germain es la sucesión A005384 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, y los primeros miembros de la sucesión son:

2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953, 1013, 1019, 1031, 1049, 1103, 1223, 1229, 1289, 1409, 1439, 1451, 1481, 1499, 1511, 1559, …

A los números primos de la forma 2p + 1, tales que p es un número primo (por lo tanto, p es un primo de Germain), se les llama números primos seguros. El nombre se deriva de la importancia de los números primos de Germain p y los primos seguros 2p + 1 en la criptografía. La sucesión de números primos seguros es la sucesión A005385 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS, y los primeros miembros de la sucesión son:

5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, 1019, 1187, 1283, 1307, 1319, 1367, 1439, 1487, 1523, 1619, 1823, 1907, 2027, 2039, 2063, 2099, 2207, 2447, 2459, 2579, 2819, 2879, 2903, 2963, …

Se desconoce, al igual que ocurre con los números primos gemelos (véase la entrada Números primos gemelos, parientes y sexis (1)), si existen infinitos números primos de Sophie Germain. Y, de nuevo, como en otros temas, se buscan números primos de Germain lo más grandes posibles. Como puede verse en la página web dedicada a los números primos y sus records, The Prime pages, el número primo de Sophie Germain más grande conocido, a día de hoy, fue obtenido en febrero de 2016, y es el número

que tiene 388.342 dígitos.

Mirando la lista de los números primos de Sophie Germain anterior podemos descubrir cuestiones como la siguiente. Si tomamos el número 2, que es un primo de Germain, resulta que el número primo seguro asociado, 2 x 2 + 1 = 5, también es primo de Germain. Más aún, el número primo seguro asociado al 5, 2 x 5 + 1 = 11, también es primo de Germain. Pero podemos continuar más, ya que 2 x 11 + 1 = 23 también es un primo de Germain. Aunque, este camino se termina aquí, puesto que 2 x 23 + 1 = 47, que ya no lo es. En cualquier caso, observamos que podemos generar cadenas de números de Germain concatenados. De hecho, a las cadenas de números primos de Sophie Germain concatenados, incluido el número primo seguro asociado al último de la cadena, en el caso anterior la cadena 2, 5, 11, 23, 47, se las llama cadenas de Cunningham, que reciben ese nombre en honor al matemático indio-británico Allan J. C. Cunningham (1842-1928). Las cadenas de Cunningham tienen la siguiente forma, si p es el número primo de Germain inicial:

Otro ejemplo de cadena de Cunningham es 89, 179, 359, 719, 1439 y 2879. En 2008, el matemático polaco Jaroslaw Wroblewski descubrió la cadena más larga conocida, a día de hoy, formada por 17 elementos. Esta cadena empieza por el número primo de Sophie Germain (con 22 dígitos):

2.759.832.934.171.386.593.519.

El poema de los números primos

Esther Ferrer es una reconocida artista cuyo arte transita entre el minimalismo y el arte conceptual, así como una pionera del arte de la performance. Su trabajo ha sido reconocido con múltiples galardones como el Premio Nacional de Artes Plásticas, en 2008, el Premio Gure Artea, en 2012, o los siguientes premios en 2014, Premio MAV (Mujeres en las Artes Visuales), Prix Marie Claire pour l’Art Contemporain y Premio Velázquez de las Artes Plásticas. Una recomendación para las personas interesadas en conocer su trayectoria artística es el documental Esther Ferrer: Hilos de Tiempo (Josu Rekalde, 2020).

En su arte podemos encontrar muchos elementos relacionados con las matemáticas, tanto como fuente de inspiración, como herramienta de creación artística, desde los números primos con los que trabaja desde la década de los años 1970, hasta el infinito en el número pi, pasando por la combinatoria, el azar, las ilusiones ópticas o la geometría. Algunas de las entradas del Cuaderno de Cultura Científica estudian esta interesante interacción, como Variaciones artísticas del teorema de Napoleón, sobre una serie de obras titulada Triángulo de Napoleón que está relacionada con un resultado clásico de la geometría, el teorema de Napoleón, o la entrada ¿Es normal el número pi?, en la cual se explica la importancia de las matemáticas en la estética de la obra Pi (2009-2010). Pero una de las herramientas de creación artística más importantes en la producción de Esther Ferrer son los números primos. De sus procesos creativos y obras relacionadas con los mismos se ha escrito en las entradas El poema de los números primos, El poema de los números primos (2) o Números primos gemelos, parientes y sexis (1), pero también en el libro La gran familia de los números (Libros de la Catarata – ICMAT – FESPM, 2021).

La instalación para la nueva plaza de acceso a Tabakalera, perteneciente a la serie El poema de los números primos, de Esther Ferrer, se construye utilizando la espiral de Ulam (véase la entrada El poema de los números primos, para una lectura más en profundidad de esta estructura geométrica plana numérica) y los números primos de Sophie Germain, que se han explicado en esta misma entrada, mediante un proceso creativo similar al de algunas de las obras de las series El poema de los números primos y Un mar de números primos, que explicaremos a continuación.

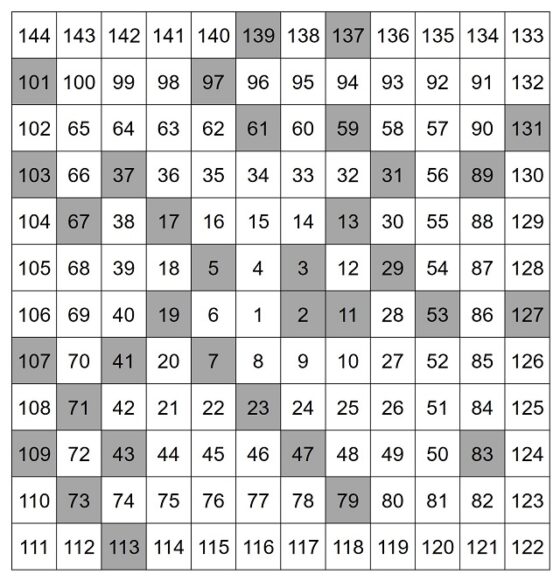
La espiral de Ulam es una estructura geométrica plana, de tipo reticular, en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos. En la siguiente imagen se muestra la espiral de Ulam hasta el número 144 (aunque es un número bajo ya se puede percibir la idea de su proceso de construcción), con las casillas de los números primos (como 2, 3, 5, 7 11, etcétera) en gris, lo que permite observar la distribución de los números primos en la misma (sobre todo para grandes retículas, como hizo el matemático polaco Stanislaw Ulam (1909-1984)).

El boceto de la instalación de Esther Ferrer, que luego se trasladará a la obra formada por baldosas ubicada en la nueva entrada de Tabakalera, consiste en una espiral de Ulam de 88 filas y 89 columnas, es decir, 7.832 casillas (desde el número 1, en el centro de la retícula cuadrada, al número 7.832 en la esquina de abajo a la izquierda). En las casillas/baldosas con números compuestos, es decir, no primos, se han borrado los números, mientras que se han dejado escritos los números primos en sus correspondientes casillas, pero además estas casillas, están pintadas de gris (la última casilla gris de la espiral de Ulam, luego de un número primo, es el 7.829), salvo algunas que serán doradas. Estas se corresponden con otro elemento importante en esta obra, como comentábamos más arriba, son los números primos de Sophie Germain. Las casillas que contienen estos números van pintadas de dorado, en lugar de gris, como homenaje a la matemática francesa (la última casilla dorada de la espiral es el número 7.823).

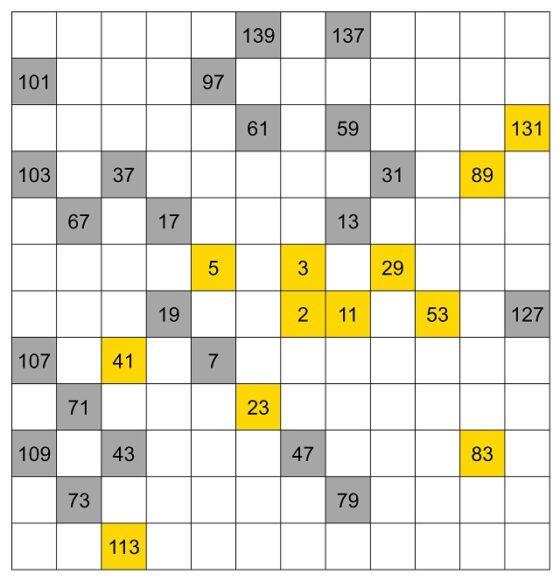
En la siguiente imagen mostramos una reconstrucción de la idea de la instalación de Esther Ferrer, pero para la pequeña retícula de 144 casillas (12 filas y 12 columnas), en la que se recoge lo explicado hasta el momento: espiral de Ulam, casillas doradas con números primos de Sophie Germain, casillas grises con números primos que no son de Germain y, por ahora, casillas blancas para los números compuestos.

El método general de Esther Ferrer, en las obras relacionadas con los números primos, consiste en generar patrones planos utilizando dos estructuras relacionadas con los mismos, la criba de Eratóstenes y la espiral de Ulam, que acabamos de mencionar para la futura instalación. En ambos casos, el patrón geométrico queda establecido de forma objetiva, por la distribución de los números primos, mientras que la artista “actúa” después sobre las zonas de números compuestos, no primos. Normalmente, crea interacciones artísticas cambiantes sobre las “lagunas de números primos”, es decir, las zonas de números compuestos, no primos, entre dos números primos consecutivos. Un ejemplo de interacción artística consiste, por ejemplo, en que, en cada casilla de un número compuesto, no primo, se dibuja una diagonal siguiendo la siguiente regla. Las diagonales tienen dos posiciones (ascendente o descendente, en el sentido del recorrido de los números) y dos colores (por ejemplo, azul y verde), y el sentido y el color de las diagonales cambian de una laguna de números primos a la siguiente. En otras obras, las diagonales van avanzando en zigzag (ascendente/descendente) de una casilla a la siguiente y es el color de las diagonales el que cambia de una laguna a otra, es decir, cambian con cada nuevo número primo. Pueden verse algunos ejemplos en las entradas mencionadas más arriba.

Sin embargo, en esta última obra Esther Ferrer ha incluido un elemento nuevo, como son los números primos de Sophie Germain y la intervención artística cambia en la misma, de diagonales en zigzag verdes a diagonales en zigzag azules, y viceversa, no en los números primos como antes, sino en los números primos de Germain. Por otra parte, las lagunas de números primos se marcan pintando media casilla, inicial y final, del color correspondiente (lo que provoca que para los números primos gemelos la casilla intermedia sea completamente azul o verde, ya que es inicial y final a la vez). En la siguiente imagen se muestra una reconstrucción para la pequeña retícula de 144 casillas.

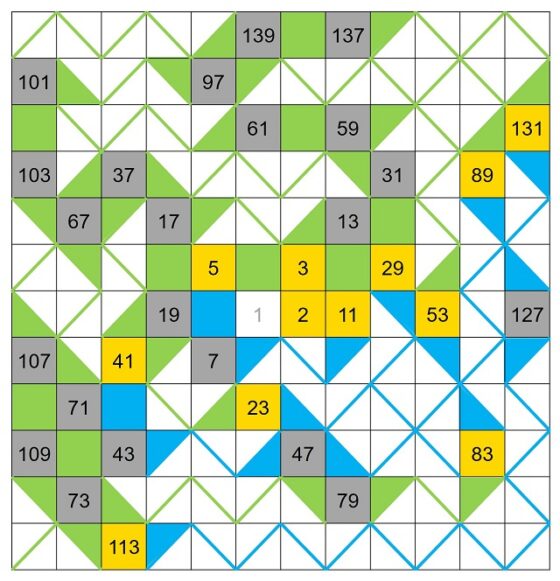
Obsérvese que, si nos vamos moviendo en espiral, como ha sido construida la espiral de Ulam, los colores de las diagonales en zigzag cambian entre los números primos de Germain, que son (menores que 144) los siguientes, 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113 y 131. Las casillas coloreadas solamente la mitad se corresponden con casillas iniciales y finales de lagunas de números primos (recordemos que son zonas de números no primos, entre un primo y el siguiente), luego las casillas monocolor se corresponden con la única casilla que está entre dos primos gemelos (parejas de números primos con solo un número par entre ellos). Por ejemplo, dos números primos de Germain consecutivos son el 41 y el 53, cuyas casillas son doradas; el color que domina las casillas entre ellos es el azul; entre el 41 y 43 la casilla es completamente azul, ya que son números primos gemelos; la pequeña laguna entre el 43 y el 47, es una pequeña zona en zigzag azul, con la casilla del 44 (inicial) con la mitad azul y la casilla del 46 (final) con la mitad azul; y algo similar en la siguiente laguna entre los números primos 47 y 53. Y entonces, en el primo de Germain 53, cambia el color al verde, hasta el siguiente, el 83.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.

2.- María Molero, Adela Salvador, Sophie Germain (1776-1831), Ed. del Orto, 2007.

3.- Lourdes Figueiras, María Molero, Adela Salvador, Nieves Zuasti, El juego de Ada. Matemáticas en las Matemáticas, Proyecto Sur, Granada. 1988.

4.- Susana Mataix, Matemática es nombre de mujer, Rubes, 2005.

5.- Xaro Nomdedeu, Mujeres, manzanas y matemáticas, Nivola, 2000.

6.- VVAA, El rostro humano de las matemáticas, Nivola, 2008.

7.- Dora Musielak, Sophie Germain, Revolutionary Mathematician, Springer, 2020.

8.- Paulo Ribenboim, The Little Book of Bigger Primes, Springer, 2004.

9.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica