En la anterior entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I) iniciamos un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci, como en el árbol genealógico de un zángano (abeja macho), en los paseos de una abeja por un panal de dos filas de celdas o en los embaldosados con fichas de dominó.
Por ejemplo, en relación con los embaldosados con fichas de dominó, mostramos que la cantidad de embaldosados rectangulares posibles de 2 filas y n columnas (es decir, una cuadrícula rectangular de tamaño n x 2), para n = 1, 2, 3, etc, con fichas de dominó (teniendo en cuenta que una ficha de dominó puede ir en horizontal, 1 x 2, o en vertical, 2 x 1), era igual a la sucesión de Fibonacci 1, 2, 3, 5, 8, … (en la siguiente imagen se muestran los 5 embaldosados rectangulares posibles de tamaño 5 x 2).
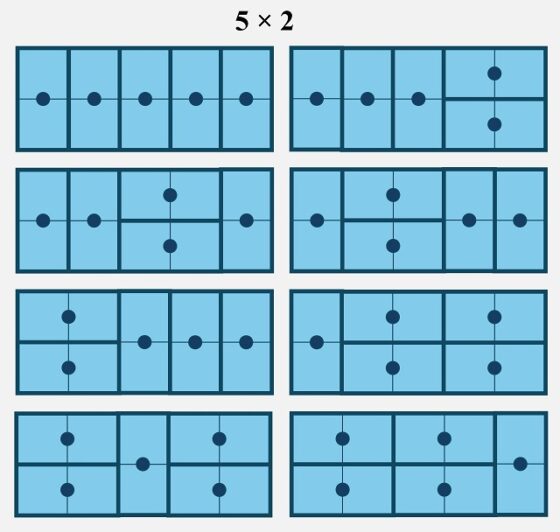
En esta entrada vamos a continuar este interesante paseo por nuevos y curiosos ejemplos.
La óptica de los rayos de luz
En el primer número, del primer volumen, de la revista Fibonacci Quarterly, del año 1963, los matemáticos austriaco-canadiense Leo Moser (1921-1970) y canadiense Max Wyman (1916-1991) propusieron el siguiente problema.
Problema: Los rayos de luz caen sobre una pila de dos placas de vidrio paralelas, un rayo pasa sin reflejarse, dos rayos (uno de cada interfaz interna opuesta al rayo) se reflejarán una vez, pero de formas diferentes, tres se reflejarán dos veces, pero de formas diferentes. Demuéstrese que el número de trayectorias distintas, que se reflejan exactamente n veces, es el número de Fibonacci Fn + 2.
Antes de nada, expliquemos el problema. En el mismo se consideran dos placas de cristal, cada una con dos superficies de reflexión. Denominamos cara 1 a la superficie de reflexión de la izquierda de la primera placa y cara 2 a la de la derecha, mientras que las caras 3 y 4 se corresponden con la segunda placa.
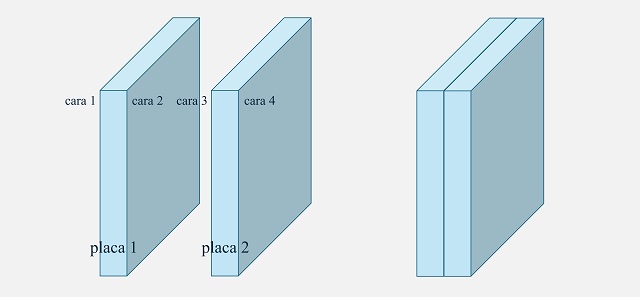
En el problema se considera un rayo de luz atravesando las placas desde uno de sus laterales, por ejemplo, desde la izquierda. Además, se estima que puesto que hay cuatro superficies de reflexión, el rayo de luz puede reflejarse interiormente de cuatro formas distintas, antes de volver a salir de nuevo, o por el lado contrario o por el mismo lado. Así, si no hay ninguna reflexión, el rayo de luz sale directamente por el otro lado, el lateral derecho (véase la siguiente imagen). Si se produce solo una reflexión, esta será en la cara 2 o en la cara 4, para después salir el rayo por el mismo lado por el que entró, el lateral izquierdo (véase la siguiente imagen). Mientras que, si se producen dos reflexiones, si la primera es en la cara 2, la segunda tendrá que ser en la cara 1, y luego la luz saldría por la derecha; mientras que, si la primera reflexión es en la cara 4, la segunda puede ser en las caras 1 o 3 (véase la siguiente imagen).
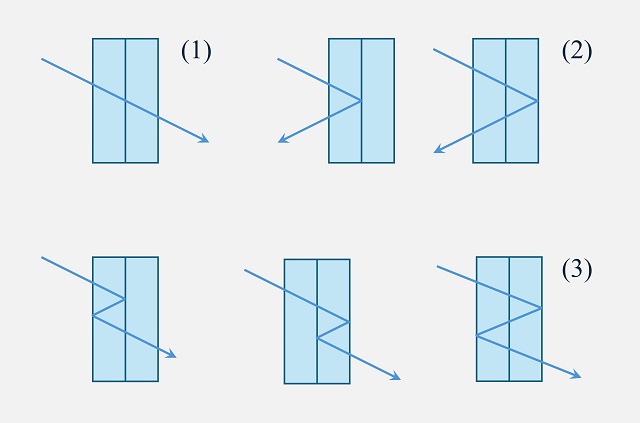
Por lo tanto, como dice el enunciado del problema, el número de trayectorias distintas si no hay reflexión es 1, si hay una reflexión es 2, mientras que si hay dos reflexiones es 3. Podemos seguir con las siguientes reflexiones, por ejemplo, para tres reflexiones, que aparece en la siguiente imagen, hay 5 trayectorias posibles.
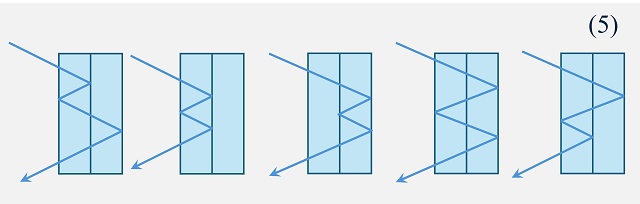
Y para cuatro reflexiones, son 8 trayectorias posibles.
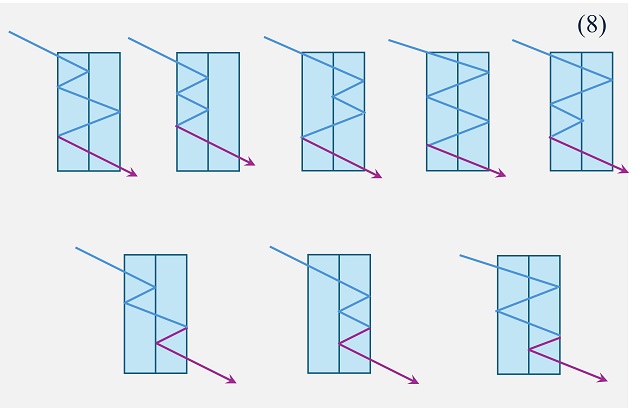
De esta manera, vamos observando paso a paso que la solución es efectivamente la sucesión de los números de Fibonacci, pero demostremos que realmente el número de trayectorias es Fn + 2, para n reflexiones. Para ello, basta demostrar que se cumple la propiedad recursiva de la sucesión de Fibonacci, que la cantidad de trayectorias para n reflexiones es igual a la suma de la cantidad de trayectorias para n – 1 y para n – 2 reflexiones.
La imagen anterior nos da la idea, ya que hemos añadido en morado cómo se pasa de los patrones de trayectorias anteriores, para n – 1 y n – 2 reflexiones (en nuestro ejemplo, 3 y 4) a los de n reflexiones. A partir de las trayectorias para n – 1 reflexiones, cuyo rayo de luz sale por el lado contrario que para n trayectorias, se añade una última reflexión para cada una de las trayectorias en la cara final que cruza después las dos placas; mientras que para n – 2 trayectorias, cuyo rayo sale por el mismo lado que para n trayectorias, se añaden dos reflexiones para cada una de las trayectorias, una en la cara final y otra en el medio (no puede ser en la cara del otro lateral, ya que esa estaría contada dentro del anterior caso), con lo cual el rayo regresa a la misma dirección de salida.
Subiendo o bajando escaleras
Imaginaos una escalera que tenéis que subir, o quizás bajar. Lo normal es que la subáis de un escalón en un escalón, pero también cabe la posibilidad de que la subáis de dos en dos si tenéis prisa o si estáis jugando, al menos yo jugaba a cosas así cuando era un niño. La cuestión es que también la podéis subir intercalando las dos maneras, de una en una y de dos en dos. El problema que nos vamos a plantear a continuación tiene que ver con las diferentes formas de subir, o bajar, una escalera.

Problema: Demostrar que el número de diferentes formas de subir la escalera con n peldaños, de manera que puedes subir uno o dos peldaños en casa paso, es el número de Fibonacci Fn + 1.
El matemático Leo Moser propuso un problema similar a este en el mismo número de la revista Fibonacci Quarterly, del año 1963, mencionado arriba. El problema dice así.
Problema: Demostrar que, teniendo en cuenta el orden, el número de diferentes formas de pagar n dólares, utilizando únicamente billetes de 1 y 2 dólares, es igual al número de Fibonacci Fn + 1.
Sumas con unos y doses
Si lo pensamos un poco, los dos problemas anteriores, nos están pidiendo que veamos las formas de obtener un número natural n como suma ordenada de unos y doses, lo que en la literatura matemática se denomina “composiciones de n con 1s y 2s”. Veamos los primeros casos, en los que observaremos claramente que aparece la sucesión de Fibonacci.

La demostración es muy sencilla, basta observar que las composiciones de n con 1s y 2s pueden obtenerse a partir de las composiciones de n – 1 y n – 2 con 1s y 2s, de la siguiente manera. Las composiciones de n con 1s y 2s que terminan en 2 (como la composición de 6 siguiente 1 + 2 + 1 + 2) son una composición de n – 2 a la que se le suma, por la derecha (ya que el orden es importante), 2 (en nuestro ejemplo 1 + 2 + 1 + 2, tenemos que se obtiene sumando 2, a la derecha, a la composición de 4, 1 + 2 + 1). Mientras que las composiciones de n con 1s y 2s que terminan en 1 (como la composición de 6 siguiente 2 + 2 + 1 + 1) son una composición de n – 1 a la que se le suma, por la derecha, 1 (en nuestro ejemplo, 2 + 2 + 1 + 2 se obtiene sumando 1, a la derecha, a la composición de 5, 2 + 2 + 1). En la siguiente imagen se muestra el caso de las composiciones de 6 con 1s y 2s, utilizando colores para separarlo (azul composiciones de 5 y verde composiciones de 4).

Por lo tanto, podríamos escribirlo en forma de teorema.
Teorema: El número de composiciones de un número natural n con 1s y 2s, es decir, el número de maneras de obtener n como suma ordenada de 1s y 2s, es igual a Fn + 1.
Si buscamos el origen de este resultado, algunas fuentes mencionan el artículo Compositions with ones and twos, de los matemáticos indio-estadounidense Krishnaswami Alladi (1955) y estadounidense Verner Emil Hoggatt Jr. (1921-1980), publicado en la revista Fibonacci Quarterly en 1975, en el que se estudian este tipo de composiciones. Sin embargo, este resultado ya era conocido con mucha anterioridad. Por ejemplo, en la segunda mitad del siglo xix matemáticos como el británico Arthur Cayley (1821-1895) estudiaron las composiciones en general, es decir, las descomposiciones de un número natural como sumas ordenadas de números. Pero podemos remontarnos más atrás en el tiempo ya que, como se explica en la entrada El origen poético de los números de Fibonacci, este resultado, relacionado con los poemas en sanscrito de la India, ya era conocido varios siglos antes, al menos en el siglo xii, pero probablemente mucho antes aún.
Si se analiza detenidamente el ejemplo de los embaldosados con fichas de dominó puede observarse que realmente es una versión de este resultado matemático. E incluso el ejemplo de la óptica de los rayos de luz, también puede traducirse de esta manera.
Fibonacci y Cayley se dan la mano
Como ya se ha mencionado más arriba, el matemático británico Arthur Cayley (de quien puede leerse la biografía Cayley, el origen del álgebra moderna) estudió las composiciones de números, en particular, obtuvo otro resultado relacionado con los números de Fibonacci.

En su artículo Teoremas sobre trigonometría y matemáticas (Messenger of Mathematics, 1876), Cayley demostró que el número de composiciones de un número n (formas de expresar n como suma ordenada de números naturales), con números estrictamente mayores que 1, es igual al número de Fibonacci Fn – 1. Veamos los primeros casos.
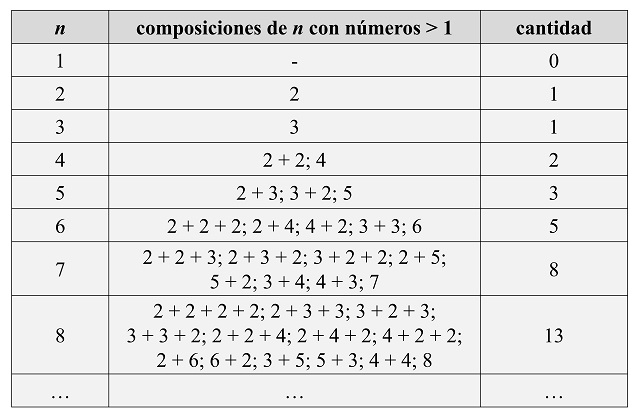
Y aún nos queda una tercera etapa de este paseo para una siguiente entrada del Cuaderno de Cultura Científica, en la que hablaremos de pintar apartamentos de dos colores, de algunos números binarios o de subconjuntos de puntos, entre otras cuestiones.

Bibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
3.- Martin Gardner, Circo matemático, Alianza editorial, 1988.
4.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica