Dijo una vez Ursula K. Le Guin que no somos nosotros los que viajamos en el tiempo, sino que es el tiempo el que viaja a través de nosotros, y tal vez ese sea el el motivo por el que todo lo relacionado con él nos fascina tanto: no lo controlamos, nos controla y lo hace, además, sin que podamos evitarlo y sin que, desde un aspecto puramente científico, tengamos todavía muy claro qué es. Sabemos que el tiempo, o la dirección en la que casi siempre lo vemos transcurrir, se manifiesta a través de los procesos irreversibles de la naturaleza, ya sean termodinámicos, cuánticos, cosmológicos… El universo que nos rodea parece tener claro hacia dónde va; resta averiguar por qué.

Más allá de la física, el tiempo determina prácticamente todos los aspectos de la experiencia humana, de ahí que haya sido un tema omnipresente en nuestras narraciones desde hace miles de años. Primero, en los mitos y leyendas, después, en la ciencia ficción. En el Mahabharata, texto hindú de alrededor del siglo III a. C, el rey Kakudmi experimenta los «efectos relativistas» de abandonar por un momento la Tierra para visitar a Brahma, el creador, y encontrarse al volver que han transcurrido varias generaciones desde su partida; algo similar a lo que le pasa a Urashima, el pescador protagonista de una leyenda japonesa del siglo XV, quien, cuando regresa a su aldea tras estar tres años en el palacio del dios dragón en el fondo del mar, se da cuenta de que, en realidad, han pasado casi trescientos cincuenta. Quedarse dormido y despertarse varios siglos en el futuro también es una forma muy típica de viajar en el tiempo en muchas historias fantásticas, o a través de la ingesta de algún tipo de sustancia con poderes milagrosos. Pero ¿en qué momento esos relatos de viajes dejaron la fantasía a un lado para intentar convertirse en ciencia? ¿Es que acaso la física permitiría algo así? ¿Existe alguna teoría que respalde la posibilidad de viajar en el tiempo, no solo hacia el futuro y más allá de la dilatación relativista? En otras palabras: ¿es posible viajar en el tiempo de alguna forma «no sobrenatural» o este tipo de historias están condenadas a existir en el ámbito de la fantaciencia para siempre?

Ha habido innumerables intentos de justificar de una manera racional la existencia de viajeros temporales en la literatura de ciencia ficción. Enrique Gaspar y Rimbau identificó el tiempo con algún tipo de fluido manipulable —algo similar al éter, aunque no exactamente eso—, en El anacronópete (1887) cuando trató de despojarlo de su halo místico. H. G. Wells, por su parte, habló de una cuarta dimensión en La máquina del tiempo (1895) —algo muy similar a lo que ya había hecho en «Los ojos del señor Davidson» (1894) con el espacio para conectar dos lugares muy alejados entre sí utilizando una especie de agujero de gusano—. Sorprendentemente, ambos vislumbraron de alguna manera el camino por el que luego iría la teoría de la relatividad general y algunas de las soluciones a las ecuaciones de Einstein. Y, así, podríamos seguir enumerando relatos y novelas hasta llegar a 1958, cuando Robert A. Heinlein escribió el que, al menos para mí, es uno de los relatos más verosímiles de viajes en el tiempo o, al menos, uno que no escandalizaría a la ciencia tanto como otros: «All you zombies—», publicado en The Magazine of Fantasy and Science Fiction en marzo del año siguiente y adaptado a la gran pantalla por Michael y Peter Spierig en 2014 con el título de Predestination.

Al que no haya leído el relato o visto la película y no le gusten los spoilers —y este es uno de esos casos en los que un mínimo destripe puede echar a perder toda la experiencia— le recomiendo que lo haga, y que vuelva más adelante a este artículo. No voy a entrar en los detalles fundamentales de la trama, pero, entre solución y solución relativista, sí es posible que haya suficientes pistas como para que alguien pueda ser capaz de desvelar el truco del prestidigitador.

Dicho esto, convirtamos la ciencia ficción en ciencia.

Entre todas estas historias de viajes temporales al pasado, al futuro, con máquina, sin máquina, de paradojas y quebraderos de cabeza con el libre albedrío hay unas de un tipo concreto que, en principio, la física no prohíbe: las de bucles temporales o, en lenguaje científico, las curvas cerradas de tipo tiempo.

En la teoría de la relatividad de Einstein, cualquier objeto que se mueve a través del espacio-tiempo tetradimensional sigue una trayectoria denominada «línea de universo». Ese espacio-tiempo normalmente lo representamos de forma geométrica con el conocido cono de luz, que, además, describe la estructura causal de determinado evento. Esto es: sus posibles pasados —causas—, su momento presente y sus posibles futuros —consecuencias—.

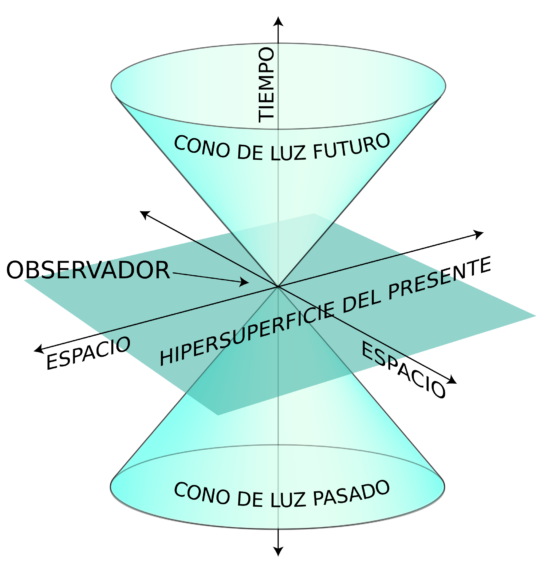
Existen, además, varios tipos de líneas de universo en función de la posición que ocupen respecto al cono de luz:

• De tipo tiempo: siempre están dentro del cono, lo que significa que describen las trayectorias de partículas que viajan a menor velocidad que la de la luz o que tienen masa.

• De tipo nulo o tipo luz: se encuentran sobre la superficie del cono y describen las trayectorias de partículas sin masa, como los fotones, que viajan a la velocidad de la luz.

• De tipo espacio: estarían fuera del cono de luz; representarían eventos desconectados causalmente o, por decirlo de otra manera, completamente «incomunicados» entre sí.

Lo que sucede en nuestro mundo se encuentra, por tanto, dentro del cono de luz y, en principio, todo tiene un punto de inicio y un punto final. Pero ¿es esa la única opción posible? Según la teoría de la relatividad general, no. Matemáticamente no hay inconveniente en que existan líneas de universo «cerradas» o bucles que empiecen y acaben en el mismo punto y se retroalimenten a sí mismos. Eso son las curvas cerradas de tipo tiempo que mencionamos antes. Y es cierto que podrían provocar algunos problemas causales, pero no siempre. En la práctica, como es obvio, este tipo de soluciones son bastante impracticables, pero ¿cuándo los límites de la realidad supusieron algún problema para un físico teórico?

Este tipo de soluciones de las ecuaciones de Einstein fueron, de hecho, de las primeras en aparecer. El físico holandés Willem Jacob van Stockum las encontró en 1937 al tratar de describir cómo sería el campo gravitacional generado por un cilindro infinito compuesto por un fluido —Gaspar y Rimbau no iba tan desencaminado— que gira alrededor de un eje. La contraposición entre fuerzas gravitacionales y centrífugas haría que, en zonas de curvatura intensa, los conos de luz se inclinaran en la dirección de rotación y… Voilà! Las líneas de universo se cerraran sobre sí mismas. Kurt Gödel encontró una solución muy similar en 1949, pero él puso a girar todo el universo, tejido del espacio-tiempo incluido, en lugar de solo una región, como Van Stockum. De nuevo, la rotación permitía la inclinación de los conos de luz y la existencia de curvas cerradas de tipo tiempo. En 1963, llegarían los agujeros negros rotatorios de Kerr, que también permitirían la existencia de bucles temporales en sus inmediaciones; en 1974, el cilindro rotatorio de Tipler…

Para entender un poco mejor qué es lo que estaría pasando en este tipo de geometrías y universos —estos últimos nada tienen que ver con el nuestro, por cierto— basta pensar en cómo los campos gravitatorios intensos afectan al tiempo dentro del marco de la relatividad general: a mayor curvatura, más lento pasa el tiempo, como ya nos enseñó la película Interstellar. Si, además, los ponemos a rotar, se produce una distorsión adicional que provoca un efecto llamado «arrastre de marcos de referencia», que como si nos lleváramos por delante el propio espacio-tiempo, pudiendo poner patas arriba su estructura causal.

No son conceptos fáciles de visualizar, ni siquiera para un físico teórico y ni siquiera con las ecuaciones y los diagramas delante, por no mencionar los quebraderos de cabeza que podría dar que se demostrara que existiera algo así. Imaginemos, simplemente, un sistema cuántico atrapado en uno de esos bucles temporales, ¿dónde quedarían su naturaleza estadística y el principio de indeterminación si, para no violar la causalidad, estuviera condenado a encontrarse siempre en el mismo estado al pasar por determinado punto?

Por si acaso, y para curarse en salud, Stephen Hawking planteó, en 1992, su conjetura de protección cronológica, que dice, básicamente, que el universo se protege a sí mismo de inconsistencias. No elimina la posibilidad de la existencia de curvas cerradas de tiempo tiempo, pero sí de aquellas que puedan provocar «¡…una paradoja temporal, lo que produciría una reacción en cadena que seguramente desarticularía el continuo espacio-tiempo y destruiría todo el universo!», como explicaría el doctor Emmett Brown en Regreso al futuro II. ¿Vas a intentar viajar al pasado para matar a tu abuelo? No pasa nada, se te encasquillará el revólver; te resbalarás con una cáscara de plátano al intentarlo, frustrando el homicidio, o descubrirás, al no desaparecer de la existencia, que hubo una infidelidad marital, pero el universo siempre evitará que se produzca una paradoja.

En junio de 2009, Stephen Hawking organizó una fiesta para viajeros del tiempo… pero envió las invitaciones después. Como no fue nadie, dio por demostrado que viajar en el tiempo es imposible. Pero ¿demostró con esta maniobra la conjetura de protección cronológica? Créditos: Discovery Communications

Está claro que los físicos se han comido bastante la cabeza para, en primer lugar, buscar maneras de que los viajes en el tiempo sean algo loquísmo, pero no tanto como podría parecer de primeras. Y, en segundo, buscarse las mañas para que esa posibilidad no provoque paradojas que destruyan el universo. ¿Sabéis quién lo hizo también? Robert A. Heinlein.

Bibliografía

Gaspar y Rimbau, E. (1887). El anacronópete. Daniel Cortezo. Biblioteca «Arte y letras».

Gödel, K. (1949). An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Reviews of Modern Physics, 21(3), 447–450

Hawking, S. W. (1992). The Chronology Protection Conjecture. Physical Review D, 46(2), 603-611.

Hawking, S., y Ellis, G. F. R. (1973). The large scale structure of space-time. Cambridge University Press.

Heinlein, R. A. (marzo de 1959). All you zombies—. The Magazine of Fantasy and Science Fiction.

Kerr, R. P. (1963). Gravitational field of a spinning mass as an example of algebraically special metrics. Physical Review Letters, 11(5), 237–238

Le Guin, U. K (2021 [1995]). Ether, OR. En Lo irreal y lo real. Minotauro.

Thorne, K. (1992). Closed timelike curves. Proceddings of the 13th International Conference on General Relativity and Gravitation.

Tipler, F. J. (1974). Rotating cylinders and the possibility of global causality violation. Physical Review D, 9(8), 2203–2206

Stockum, W. J. van (1937). The gravitational field of a distribution of particles rotating around an axis of symmetry. Proceedings of the Royal Society of Edinburgh, 57, 135.

Wells, H. G. (1895). La máquina del tiempo. William Heinemann.

.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.