La prueba, que se sabe que es tan difícil que un matemático una vez ofreció 10 martinis a quien pudiera encontrarla, conecta la mecánica cuántica con estructuras matemáticas infinitamente intrincadas.

Un artículo de Lyndie Chiou y Joseph Howlett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

En 1974, cinco años antes de escribir su libro Gödel, Escher, Bach: un eterno y grácil bucle, con el que ganó el Premio Pulitzer, Douglas Hofstadter era estudiante de doctorado en Física en la Universidad de Oregón. Cuando su director de tesis se fue a un año sabático a Ratisbona (Alemania), Hofstadter decidió acompañarle con la esperanza de practicar su alemán. Ambos se unieron a un grupo de brillantes físicos teóricos que se devanaban los sesos con un problema concreto de la teoría cuántica: querían determinar los niveles de energía de un electrón en una red cristalina sometida a un campo magnético.

Hofstadter era el “bicho raro”, incapaz de seguir la línea de razonamiento de los demás. Con el tiempo se alegró de ello. “Parte de mi suerte fue que no podía seguirles el ritmo”, comenta. “Estaban demostrando teoremas, pero no tenían nada que ver con la esencia de la situación”.

En lugar de intentar demostrar teoremas, Hofstadter decidió probar un enfoque más práctico. Se propuso hacer cálculos numéricos con una HP 9820A, una calculadora de sobremesa —una especie de ordenador primitivo— que pesaba casi 20 kilos y que podía programarse para realizar operaciones complejas.

Lo necesitaba para resolver una formulación concreta de la ecuación de Schrödinger, núcleo de la mecánica cuántica. Al introducir cierta información sobre un electrón y su entorno, la ecuación describe cómo se comportará. En particular, sus soluciones indican la cantidad de energía que el electrón puede tener.

En el caso que interesaba a Hofstadter, la ecuación de Schrödinger incluía una variable llamada alfa, el producto de la intensidad del campo magnético por el área de una celda de la red. Alfa recoge la información sobre las fuerzas que actúan sobre el electrón.

El grupo de matemáticos en Alemania sabía que, cuando alfa era un número racional —es decir, un entero o una fracción—, resolver la ecuación era arduo pero posible (siempre que se dispusiera de una calculadora suficientemente potente). Pero cuando alfa era irracional, lo que significa que no puede escribirse como fracción, no tenían ni idea de cómo abordarlo.

Hofstadter, en lugar de luchar con el caso irracional como sus colegas, empezó con lo que sí conocía. Programó su calculadora para que tomara un valor racional de alfa como entrada y le devolviera un resultado impreso en un rollo de papel: los niveles de energía permitidos y prohibidos del electrón.

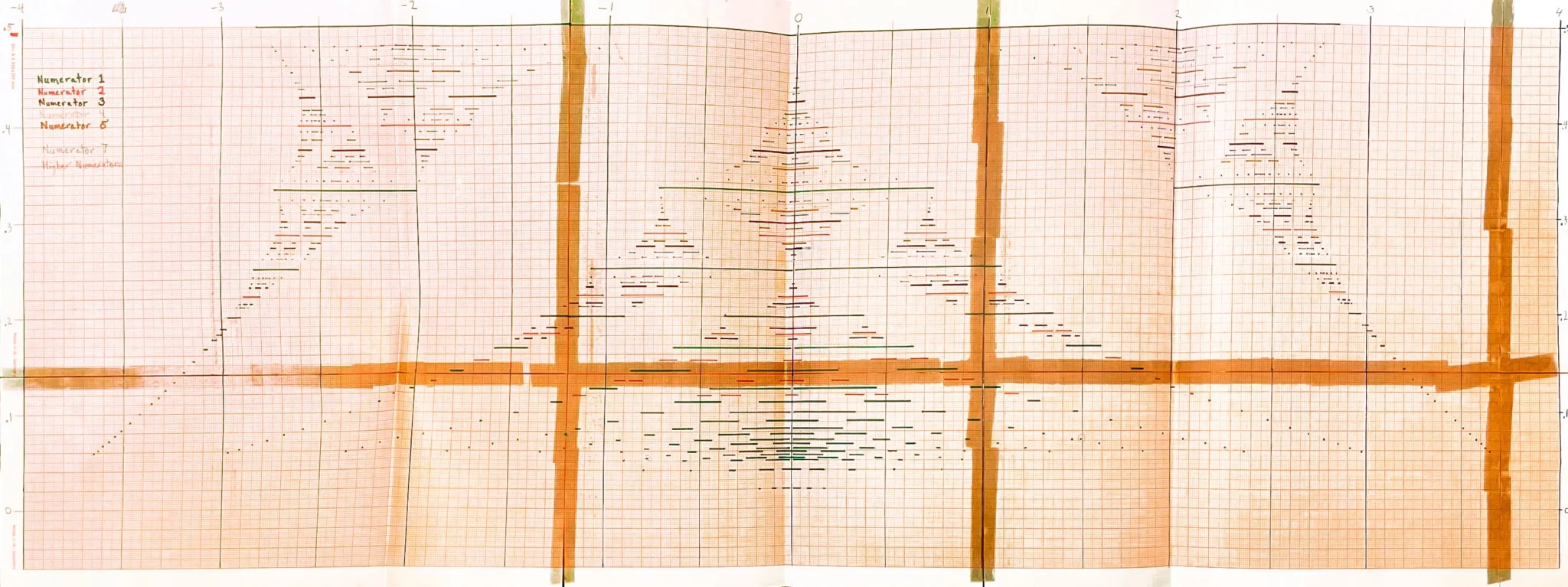
Cada noche dejaba la calculadora funcionando, y a la mañana siguiente regresaba para encontrarse con una larga tira de papel que listaba las energías permitidas para cada valor racional de alfa que había introducido. Pegó varias hojas de papel cuadriculado y, con un rotulador, comenzó a representar meticulosamente esos valores. Esa imagen acabaría siendo conocida como la mariposa de Hofstadter, por el parecido del espacio en blanco del gráfico con las alas del insecto.

Sus colegas no entendían el sentido de aquel trabajo tan laborioso. Se burlaban diciendo que intentaba hilar oro a partir de paja y apodaron a su calculadora “Rumpelstilzchen” [*].

Incluso su director de tesis despreció el esfuerzo tachándolo de “numerología” y amenazó con retirarle la financiación. “Estaba insinuando que me comportaba como un supersticioso y que decía tonterías”, recuerda Hofstadter. “Buscando significado y patrones en los números cuando no existen”.

Pero la mariposa que empezaba a emerger en su papel milimetrado le intrigaba. Observó que, al introducir una fracción, las energías permitidas se interrumpían con largos tramos de valores prohibidos. Cuanto más complicada era la fracción, con más cifras en el denominador, más interrupciones aparecían. Los valores de energía empezaban a formar un patrón visualmente impactante: un fractal, es decir, una estructura en la que las partes más pequeñas se parecen al todo.

Su intuición le decía que aquello reflejaba una verdad matemática profunda. “Me quedó muy claro que tenía un tigre agarrado por la cola”, recuerda. Reconocía al tigre: era el conjunto de Cantor.

El conjunto recibe su nombre del matemático Georg Cantor, que lo popularizó en 1883 siguiendo una regla sencilla: toma un segmento de recta, divídelo en tres partes iguales y borra el tercio central. Quedan así dos segmentos separados por un hueco. Luego se borra el tercio central de cada uno de ellos, y así sucesivamente. Si se repite el procedimiento infinitas veces, se obtiene un conjunto infinito de puntos, dispersos como polvo a lo largo de la recta numérica.

Hofstadter nunca introduciría un valor irracional de alfa. Los números irracionales no pueden expresarse como fracción: se necesitarían infinitas cifras en el numerador o en el denominador, algo imposible de programar en la calculadora. Pero notó que, a medida que los valores racionales de alfa se aproximaban más y más a un irracional, el conjunto de energías permitidas —las franjas de tinta en cada fila de su mariposa— se parecía cada vez más a un conjunto de Cantor. Y así, planteó la hipótesis de que, cuando alfa fuera irracional, los niveles de energía posibles formarían un auténtico conjunto de Cantor.

Años más tarde, dos matemáticos prominentes llegaron a la misma conclusión desde una dirección muy diferente. Barry Simon y Mark Kac habían estado estudiando lo que llamaban funciones casi periódicas. Las funciones periódicas, como la onda sinusoidal, repiten sus valores una y otra vez. Pero una función casi periódica describe un recorrido que se aproxima a repetirse, sin llegar nunca a hacerlo.

En 1981, Kac y Simon se reunieron a almorzar y empezaron a hablar de la versión de la ecuación de Schrödinger que Hofstadter y sus colegas intentaban resolver. Cuando alfa era irracional, la ecuación se convertía en una función casi periódica. Era exactamente el tipo de fenómeno que ellos estudiaban. Y, basándose en lo que sabían sobre funciones casi periódicas, Hofstadter tenía razón: los niveles de energía permitidos debían formar un conjunto de Cantor cuando alfa fuera irracional.

Pero Simon y Kac tampoco podían demostrarlo. Kac dijo que invitaría a 10 martinis a quien lo consiguiera. Simon empezó a difundir la oferta de Kac, y el problema pasó a conocerse como la conjetura de los diez martinis.

Con los años, los matemáticos fueron arrancando pequeños avances, demostrando la conjetura para ciertos valores irracionales de alfa (pero no para todos). Simon anunció uno de esos resultados intermedios en 1982. Kac le pagó tres martinis. Cuando Kac murió en 1984, el problema seguía abierto. Una demostración que valiera los diez martinis completos no aparecería hasta 20 años después.

Solo un poco sucia

En 2003, Svetlana Jitomirskaya, que llevaba años estudiando la función casi periódica incrustada en la ecuación de Schrödinger, acababa de abandonar su objetivo de toda la vida: demostrar la conjetura de los diez martinis. Un año antes, un competidor llamado Joaquim Puig la había demostrado para todas las clases de valores irracionales de alfa, salvo unas pocas. Y lo había hecho utilizando técnicas que ella misma había publicado antes. “Me tiraba de los pelos”, confiesa. “Todo el trabajo duro estaba en mi demostración, y luego llega él con este argumento tan elegante”.

Así que se sorprendió cuando un joven matemático de 26 años, Artur Avila, la visitó y le propuso trabajar juntos en los valores de alfa que quedaban. “Le dije que sería muy difícil, muy largo y que a nadie le iba a importar”, cuenta.

Se equivocaba. Su demostración, que colgaron en línea en 2005, fue publicada finalmente en Annals of Mathematics, la revista más prestigiosa del área. Avila acabaría ganando una Medalla Fields en parte por este trabajo.

Decidieron honrar por sí mismos el contrato de los diez martinis. “Tuvimos abundantes bebidas de celebración, martinis incluidos”, recuerda Jitomirskaya.

Pero en cierto sentido, la demostración no era del todo satisfactoria. Jitomirskaya y Avila habían utilizado un método que solo servía para ciertos valores irracionales de alfa. Al combinarlo con una demostración intermedia anterior, podían decir que el problema estaba resuelto. Pero aquella prueba combinada no era elegante: parecía una colcha de retales, cada trozo cosido con un argumento distinto.

Además, las demostraciones solo resolvían la conjetura tal como se había planteado originalmente, lo que implicaba hacer suposiciones simplificadoras sobre el entorno del electrón. La situaciones más realistas son mucho más complicadas: los átomos en un sólido se disponen en patrones complejos y los campos magnéticos no son constantes. “Lo verificas para este modelo concreto, pero ¿qué tiene eso que ver con la realidad?”, comenta Simon Becker, matemático del Instituto Federal Suizo de Tecnología de Zúrich.

Estas situaciones más realistas requieren modificar la parte de la ecuación de Schrödinger donde aparece alfa. Y al hacerlo, la demostración de los diez martinis deja de funcionar. “Esto siempre me resultó inquietante”, admite Jitomirskaya.

La ruptura de la demostración en contextos más amplios también sugería que los bellos patrones fractales que habían aparecido —los conjuntos de Cantor, la mariposa de Hofstadter— no eran más que una curiosidad matemática, algo que desaparecería en cuanto la ecuación se hiciera más realista.

Avila y Jitomirskaya pasaron a otros problemas. Incluso Hofstadter dudaba. Si algún experimento llegaba a ver su mariposa, había escrito en Gödel, Escher, Bach, “sería la persona más sorprendida del mundo”.

Pero en 2013, un grupo de físicos de la Universidad de Columbia capturó su mariposa en el laboratorio. Colocaron dos capas delgadas de grafeno en un campo magnético y midieron los niveles de energía de los electrones del grafeno. El fractal cuántico emergió en todo su esplendor. “De repente pasó de ser una fantasía de los matemáticos a algo práctico”, dice Jitomirskaya. “Resultó muy desconcertante”.

Quería explicarlo con matemáticas. Y un nuevo colaborador tenía una idea de cómo hacerlo.

Otra ronda, con un giro

En 2019, Lingrui Ge se unió al grupo de Jitomirskaya. Se había inspirado tanto en el trabajo que ella y Avila hicieron sobre el problema de los diez martinis como en una línea de investigación que Avila había intentado seguir desde entonces.

Avila estaba cansado de los enfoques fragmentarios que los matemáticos usaban para entender las funciones casi periódicas. Comenzó a desarrollar lo que llamó una “teoría global”: una forma de descubrir estructuras de nivel superior en todo tipo de funciones casi periódicas, que luego pudiera usar para resolver clases enteras de funciones de una sola vez.

Para ello, asociaba un objeto geométrico a una función casi periódica dada y estudiaba sus propiedades. Se dio cuenta de que algunas de esas propiedades geométricas podían ayudarle a resolver la función original.

Pero solo funcionaba para ciertos tipos de funciones. No podía manejar los cálculos que requería el problema de los diez martinis. No estaba claro que alguna vez pudiera.

Eso se debía a que, para demostrar la conjetura de los diez martinis, los matemáticos tenían que transformar primero la ecuación de Schrödinger en una ecuación relacionada llamada su dual, y luego resolver esa nueva ecuación. La teoría de Avila no decía nada sobre la estructura de alto nivel de la dual.

O eso creía él. Pero Ge estaba intrigado por los objetos geométricos que Avila había descrito. Sospechaba que otras propiedades de esos objetos escondían más información aún, información que podía iluminar aspectos de la ecuación dual. “Podía ver que era una teoría muy bella e importante”, dice Ge.

Él y Jitomirskaya —junto con Jiangong You y Qi Zhou, de la Universidad de Nankai en China— encontraron una nueva forma de interpretar el objeto geométrico de Avila y aplicarlo a la dual. Esto hizo la teoría mucho más potente. También permitió que Ge, Jitomirskaya y You escribieran una sola demostración que resolvía versiones del problema de los diez martinis en muchos contextos distintos. Ya no hacía falta la colcha de retales.

El resultado consolida la mariposa de Hofstadter como un fenómeno real. El mundo abstracto de la teoría de números demuestra su poder en la física.

Los matemáticos han utilizado desde entonces su versión de la teoría global de Avila para resolver otros dos problemas clave en el área. Predicen que esto es solo el comienzo de lo que podrán hacer con el método que han descubierto. “Encontramos este misterio oculto tras la teoría global”, afirma Ge. “Era como un faro en un mar oscuro que nos mostró el rumbo correcto”.

[*] Nota del traductor: Rumpelstilzchen (Rumpelstiltskin, en castellano) es el nombre alemán original de un cuento recopilado por los hermanos Grimm. Rumpelstiltskin era un duende que hilaba paja transmutándola en oro.

El artículo original, ‘Ten Martini’ Proof Uses Number Theory to Explain Quantum Fractals, se publicó el 25 de agosto de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.

Traducido por César Tomé López