Uno de los quebraderos de cabeza de cualquier persona que viaje hoy en día en avión son las maletas. Hace un tiempo, en cualquier billete de avión, estaba incluido el llamado equipaje de mano o equipaje de cabina, junto con una pieza personal, que podía ser un pequeño bolso o la maleta del ordenador, mientras que en la actualidad nos cobran por ese equipaje de mano y es el antiguo complemento personal, el bolso debajo del asiento, el que únicamente es gratis. Además, está el tema de las medidas de los bolsos personales (debajo del asiento) y de las maletas de cabina, sobre todo por lo estrictas que se han puesto algunas compañías al respecto.

Como podemos observar hay diferentes medidas para las distintas aerolíneas, lo cual hace que casi tengamos que tener una colección de maletas de distintas dimensiones para viajar. Hace unos años, y aún hay varias compañías que lo mantienen, existía una norma general (que era el estándar internacional de la IATA = Asociación Internacional de Transporte Aéreo), por encima de las recomendaciones particulares de cada compañía, que consistía en que las medidas de la maleta de cabina debían ser tales que su suma no excediera los 115 centímetros, es decir, ancho + largo + alto (de la maleta) debía medir menos, o igual, que 115 cm.

En esta entrada vamos a reflexionar sobre este problema, tomando como punto de partida uno de los libros del matemático y divulgador barcelonés Claudi Alsina, titulado Contar bien para vivir mejor (Rubes, 1998), que utilizó el problema de las medidas de las maletas de mano como ejemplo cotidiano para hablar de algunas cuestiones sencillas de geometría. De hecho, este ejemplo es realmente una excusa para realizar, desde el Cuaderno de Cultura Científica, un pequeño homenaje a este excelente matemático y gran divulgador.

Homenaje a Claudi Alsina

El pasado 16 de noviembre falleció el matemático barcelonés Claudi Alsina Catalá (1952-2025), uno de los divulgadores de las matemáticas españoles más importantes de las últimas décadas.

Fue uno de los pioneros de la divulgación matemática en España. Por ejemplo, en relación con la publicación de libros de divulgación de las matemáticas, antes del Año Mundial de las Matemáticas, en el año 2000, se publicaban muy pocos libros en España y prácticamente la totalidad eran traducciones de autores extranjeros, salvo un pequeño grupo de matemáticos españoles entre los que estaba Claudi Alsina, junto a Miguel de Guzmán, Antonio Durán, Luis Balbuena o Susana Mataix. Entre sus libros de esa época estaban algunos clásicos de la divulgación como Los matemáticos no son gente seria (Rubes, 1996) o Contar bien para vivir mejor (Rubes, 1998), libros de cuentos matemáticos como Del número 0 al 99 (Grao, 1993) o Para Elisa; Tres lobos; y Un cerdito feroz (Proyecto Sur, 1999), así como una cantidad importante de libros relacionados con la enseñanza y didáctica de las matemáticas.

A partir del año 2000, Claudi Alsina se convirtió en un autor de divulgación científica muy prolífico, exitoso y admirado, con títulos como El club de la hipotenusa: Un paseo por la historia de las matemáticas a través de sus anécdotas más divertidas (Ariel, 2008), Geometría para turistas: Una guía para disfrutar de 125 maravillas mundiales y descubrir muchas más (Ariel, 2009), Asesinatos matemáticos: Una colección de errores que serían divertidos si no fuesen tan frecuentes (Ariel, 2010), Demostraciones con encanto: Un viaje por las matemáticas elegantes (SM, 2011, junto a Roger B. Nelsen), Mateschef: Un sofrito de números y formas para chefs y gourmets (Ariel, 2015), Todo está en los números (Ariel, 2017), Geometría y moda (Catarata, 2019), Geometría y diseño (Catarata, 2022), Los matemáticos serios son los que no se ríen nunca: Personalidades excéntricas, pecados inconfesables, anécdotas y retos recreativos (Ariel, 2024), entre otros.

El último libro publicado por el matemático catalán ha sido El tercer lunes de enero es el día más triste del año. Matemáticas & Fake News (Ariel, 2025), que acaba de llegar a las librerías y que plantea como las matemáticas pueden ayudarnos a combatir las fake news.

Además, ninguna persona que haya escuchado alguna de sus emotivas conferencias la olvidará jamás. Y como decía muchas veces Claudi Alsina, lema que ha incluido en su carta de despedida en la Revista SUMA (de la Federación Española de Sociedades de Profesores de Matemáticas):

La matemática rigurosa se hace con la mente,

La matemática hermosa se enseña con el corazón.

Contar bien para vivir mejor

Volviendo al problema de las medidas de las maletas de cabina, este fue uno de los temas que incluyó Claudi Alsina en su libro Contar bien para vivir mejor (Rubes, 1998), en ese estilo suyo, tan característico, de utilizar ejemplos de la vida cotidiana para divulgar las matemáticas.

Como decíamos al principio de esta entrada del Cuaderno de Cultura Científica, hace un tiempo, la norma general para las medidas de las maletas de mano era la siguiente:

ancho + largo + alto ≤ (menor o igual) 115 cm.

Por ejemplo, hacia el año 2010, cuando incluí este hermoso ejemplo en mi conferencia Matemáticas para andar por casa, compañías aéreas como Iberia, Spanair o Aireuropa, entre otras, acompañaban la norma general con una recomendación, que para estas tres aerolíneas era 20 x 40 x 55 cm (Iberia), 25 x 40 x 50 cm (Spanair), 25 x 35 x 55 cm (Aireuropa), las tres distintas, pero la suma de sus dimensiones era el límite general de 115 cm.

Esa norma general permitía las medidas recomendadas por Iberia, Spanair y Aireuropa, así como las recomendaciones de las demás compañías aéreas, pero incluso otras medidas tan poco habituales como una caja cuadrada de lado igual a 115 / 3 cm, aproximadamente 38,33 cm, o una barra cuadrada alargada de 1 x 1 x 13 cm.

Pero, como destacaba Claudi Alsina en su libro, las diferentes medidas de las maletas, aunque todas ellas tomen el valor máximo ancho + largo + alto = 115, dan lugar a diferentes volúmenes. Así la maleta de las medidas sugeridas por Iberia, 20 x 40 x 55 cm, contenía un volumen (recordemos que el volumen de una caja rectangular -paralelepípedo- es igual al producto de las tres medidas ancho x largo x alto) de 20 x 40 x 55 = 44.000 centímetros cúbicos (lo que es igual a 44 decímetros cúbicos o litros), la maleta sugerida por Spanair contenía un volumen de 25 x 40 x 50 = 50.000 centímetros cúbicos, mientras que la maleta de Air Europa contenía un volumen de 25 x 35 x 55 = 48.125 centímetros cúbicos.

En conclusión, con una maleta de Spanair se podía meter más contenido en la maleta que con las maletas de las otras compañías. De hecho, con la maleta de Spanair se disponía de un 13,6% más de volumen que con la maleta de Iberia.

El problema de optimización del volumen

Por lo tanto, como el valor máximo de la norma IATA permitía varias medidas para las maletas de mano que daban lugar a diferentes volúmenes, las personas que viajaban en avión podían tener interés en comprar una maleta cuyas medidas cumpliesen la norma general, pero el volumen fuese el mayor posible y así tener más espacio para su ropa. En el libro Contar bien para vivir mejor, Claudi Alsina planteaba una cuestión lógica como la siguiente:

¿Qué medidas debe tener una maleta, que cumpla la norma de las aerolíneas con su valor máximo, es decir, ancho + largo + alto = 115 cm, para contener el máximo volumen posible?

Antes de abordar la cuestión, un asunto de notación matemática. Vamos a llamar x al valor del ancho, y al valor del largo y z al valor del alto de una maleta. De esta manera, en el problema estamos considerando las maletas con medidas (x, y, z) tales que

Y queremos conocer qué medidas de las maletas, es decir, qué valores (x, y, z), nos dan el mayor volumen posible. Y recordemos que la fórmula del volumen de una maleta (cuya figura geométrica es un paralelepípedo) es

Podemos intuir que el mayor volumen se obtiene para la maleta cúbica de 115/3 cm de lado (aproximadamente 38,33 cm), cuyo volumen sería 56.328,7 centímetros cúbicos, claramente mayor que los tres volúmenes anteriores para las aerolíneas españolas. Pero, como hacemos siempre en matemáticas, esa afirmación, de que el mayor volumen se obtiene con la maleta cúbica hay que demostrarla.

Para esa demostración se utiliza la siguiente desigualdad matemática, la desigualdad entre la media geométrica y la media aritmética de tres valores x, y, z:

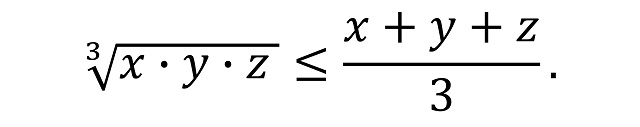
Por lo tanto, si tomamos una maleta de medidas (x, y, z) y utilizamos la fórmula anterior, pero elevada al cubo, se obtiene lo siguiente:

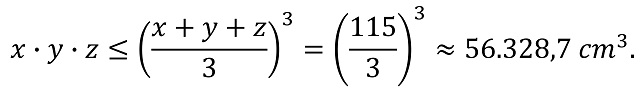
En conclusión, cualquier maleta de medidas (x, y, z), tales que x + y + z = 115 cm, su volumen es menor, o igual, que 56.328,7 centímetros cúbicos. Por lo tanto, la maleta cúbica es la de mayor volumen.

Otra cosa distinta era que, a pesar de cumplir la norma general, nos hubiesen dejado subir la maleta cúbica en el avión como maleta de mano, puesto que no cabía en el compartimento de equipaje de cabina del avión, situado en la zona superior. Aquí nos encontramos de nuevo con la astucia de la mente matemática de Claudi Alsina, que planteaba en su libro Contar bien para vivir mejor utilizar dos maletas juntas de tamaño 38,3 x 38,3 x 19,15 cm, que juntas tendrían un volumen máximo, pero luego dentro del avión se podrían separar y ser colocadas en la zona para el equipaje de cabina.

Un dispositivo para controlar las maletas

Recordemos que estamos hablando de un momento en el que, aunque las compañías aéreas aconsejaban unas medidas concretas para las maletas de cabina, por ejemplo, las comentadas anteriormente 20 x 40 x 55 cm (Iberia), 25 x 40 x 50 cm (Spanair), 25 x 35 x 55 cm (Air Europa), existía una norma general (estándar internacional de la IATA) que era que la maleta de medidas (x, y, z) tenía que cumplir que la suma de las tres medidas x + y + z fuese menor, o igual, que 115 centímetros.

El problema estaba en que siendo la norma general ancho + largo + alto menor, o igual, que 115 cm, el dispositivo que utilizaba cada compañía para controlar si las maletas de los pasajeros cumplían la normativa era un dispositivo con forma de paralelepípedo (caja rectangular, como en la anterior imagen) con las medidas de su recomendación. Así, en la caja de Iberia, adaptada para las medidas 20 x 40 x 55 cm, podían tener problemas las maletas de Spanair o Aireuropa, que eran más anchas, de 25 cm, así como maletas con otras medidas, incluyendo la maleta cúbica de 38,33 cm de lado, que, aunque fuese extraña y difícil de incluir en la zona de equipaje de mano, estaba dentro de la norma.

Ante esta situación, cuando preparé mi charla Matemáticas para andar por casa, me planteé la siguiente cuestión:

¿Es posible diseñar un dispositivo para que la compañía aérea compruebe que las medidas del equipaje (sin medirlas) cumplen la norma general?

puesto que el sistema de la caja rectangular realmente no era efectivo. De hecho, quizás por este motivo se ha ido eliminando la norma general de que ancho + largo + alto sea menor, o igual, que 115 cm, por medidas más concretas, en algunos casos un poco mayores.

En mi siguiente entrada del Cuaderno de Cultura Científica abordaremos la anterior cuestión, mostrando que sí se podía diseñar un dispositivo para comprobar que las medidas del equipaje de mano (x, y, z) cumplían la norma general, para lo cual necesitamos conocer qué son las coordenadas cartesianas y cuál es la ecuación de un plano.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica