En la anterior entrada del Cuaderno de Cultura Científica titulada A vueltas con el equipaje de mano (I) estuvimos hablando de las medidas de las maletas de cabina. En la actualidad cada compañía aérea tiene establecidas unas medidas concretas (ancho x largo x alto) para el equipaje de mano que debe ser utilizado en sus aviones. Por ejemplo, para British Airways y EasyJet son 25 x 45 x 56 cm, para Iberia son 25 x 40 x 56 cm, para Lufthansa 23 x 44 x 55 cm, para Vueling y Ryanair 20 x 40 x 55 cm, para American Airlines 23 x 36 x 56 o para Air Europa, Air France o KLM 25 x 35 x 55 cm, que, aunque todas puedan estar alrededor de unas ciertas medidas, tienen diferencias significativas en algunos casos.

Como comentábamos en la anterior entrada, hace unos años, y aún hay compañías que lo mantienen, existía una norma general (que era el estándar internacional de la IATA = Asociación Internacional de Transporte Aéreo), por encima de las recomendaciones particulares de cada compañía (que, en algunos casos, en aquella época eran algo menores que las actuales), que consistía en que las medidas de la maleta de cabina debían ser tales que su suma no excediera los 115 centímetros, es decir, ancho + largo + alto (de la maleta) debía medir menos, o igual, que 115 cm. Esto es,
![]()
siendo x = ancho, y = largo, z = alto.
Un dispositivo para controlar las maletas
Como pusimos de manifiesto en la reflexión final de la anterior entrada, el problema estaba en que siendo la norma general ancho + largo + alto menor, o igual, que 115 cm, el dispositivo que utilizaba cada compañía para controlar si las maletas de los pasajeros cumplían la normativa era un dispositivo con forma de paralelepípedo (caja rectangular, como en la siguiente imagen) con las medidas de su recomendación, que en aquella época se ajustaban a que la suma de las medidas (ancho, largo y alto) fuese 115 cm. Así, la caja de Iberia estaba adaptada para las medidas que recomendaba en esa época 20 x 40 x 55 cm, pero en esa caja podían tener problemas las maletas recomendadas por Spanair (25 x 40 x 50 cm) o Air Europa (25 x 35 x 55 cm), que eran más anchas, de 25 cm, así como maletas con otras medidas, incluyendo la maleta cúbica de 38,33 cm de lado, que, aunque fuese extraña y difícil de incluir en la zona de equipaje de mano (véase la entrada A vueltas con el equipaje de mano (I)), estaba dentro de la norma general.

Por este motivo, cuando hace unos cuantos años (alrededor de 2010) preparé mi charla Matemáticas para andar por casa, me planteé la siguiente cuestión:
¿Es posible diseñar un dispositivo para que la compañía aérea compruebe que las medidas del equipaje (sin medirlas) cumplen la norma general?
puesto que el sistema de la caja rectangular realmente no era efectivo. De hecho, quizás por este motivo se ha ido eliminando la norma general de que ancho + largo + alto sea menor, o igual, que 115 cm, por medidas más concretas, en algunos casos algo mayores, que dan más flexibilidad.

La solución para la regla general no era la estructura de caja rectangular utilizada, que como fuente de información orientativa podía ser válida, o estar tomando las medidas de cada maleta, que hubiese convertido el sistema en un suplicio para las trabajadoras de la compañía aérea, sino un dispositivo que, como veremos, derivaba del conocimiento de lo que son las coordenadas cartesianas y la ecuación cartesiana de un plano.
No se trata en esta entrada de intentar establecer un mecanismo que se podía, o no, haber utilizado, sino mostrar como el análisis matemático de un problema puede ofrecer una solución al mismo. Una vez obtenida esa solución la empresa implicada puede decidir desarrollarla, o no, en función de múltiples factores que tendrá que tener en cuenta.
El problema en dos dimensiones
Para intentar simplificar la cuestión y facilitar su comprensión, vamos a pensar en el problema en dos dimensiones, en cuyo caso, en lugar de una maleta tendremos un objeto rectangular (cuyas dimensiones son el ancho y el largo), por ejemplo, el marco de una fotografía o un cuadro.

Por lo tanto, una regla equivalente al estándar de IATA para las maletas podría ser que la suma de las medidas del marco sea menor, o igual, que 35 centímetros. De esta manera entrarían dentro de lo permitido medidas habituales como 13 x 18 cm o 15 x 20 cm. En consecuencia, se trata de crear un dispositivo para controlar que los marcos de las fotografías cumplan esa regla. Pensemos que quizás, esto podría ser útil en una fábrica de marcos para separar los marcos por tamaños o alguna otra situación equivalente.
Para analizar matemáticamente esta cuestión vamos a introducir primero las coordenadas cartesianas del plano y después la ecuación de una recta en el plano utilizando las coordenadas cartesianas.
Coordenadas cartesianas
Para definir estas coordenadas en el plano debemos de partir de dos rectas perpendiculares, que van a ser los denominadas “ejes de coordenadas” (el eje X o eje de abscisas –horizontal– y el eje Y o eje de ordenadas –vertical–), a cuyo punto de corte se le denomina origen (O). Entonces, las coordenadas cartesianas (rectangulares) permiten determinar la posición de cada punto del plano P en función de dos números (x, y) que expresan la distancia del punto a los dos ejes coordenados (x la distancia del punto P al eje Y e y la distancia al eje X). En esta imagen vemos algunos ejemplos que nos ayudan a entender mejor esta idea (el signo negativo indica si se está en una parte o en otra respecto a los ejes, aunque para lo que nos ocupa aquí solo hablaremos de coordenadas positivas). Por ejemplo, el punto (3,2) dista 3 unidades del eje Y y 2 unidades del eje X.
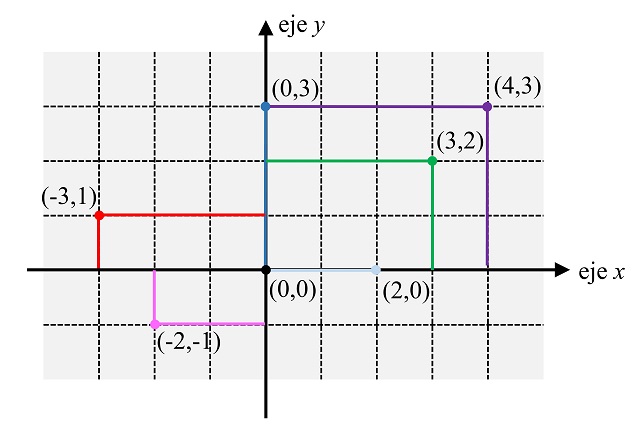
Nos podemos cuestionar el motivo por el cual es útil hablar de coordenadas cartesianas en este problema. Seguramente, la imagen anterior nos dará ya una idea del motivo. Imaginemos que tenemos un plano coordenado y colocamos un marco de manera que uno de sus vértices esté apoyado en el origen y dos de sus lados estén apoyados en los ejes coordenados, como en la siguiente imagen, de manera que el ancho se apoye en el eje X y el largo en el eje Y.
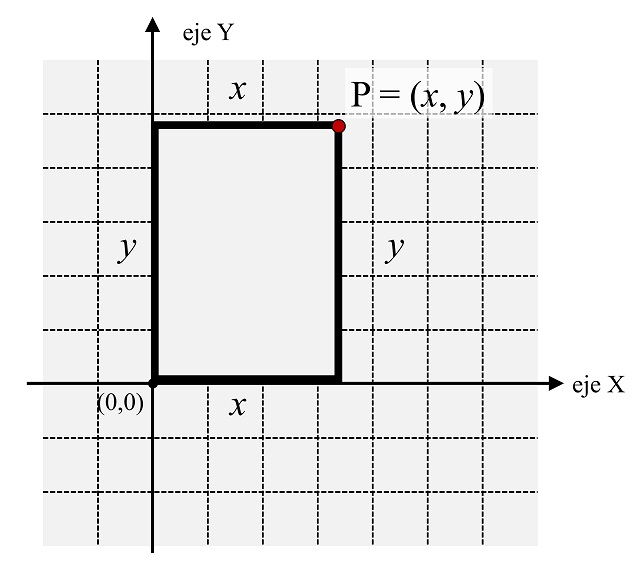
De esta manera, como se muestra en la imagen anterior, las medidas del marco de una fotografía (x, y), siendo x el ancho e y el largo, determinarán el punto P = (x, y) del plano, que es la posición del vértice opuesto al apoyado en el origen. Y recíprocamente, dado un punto cualquiera del plano P = (x, y), este determinará las medidas concretas de un marco fotográfico, colocado como en la situación anterior.
La ecuación de una recta
Dicho esto, ahora vamos a explicar qué es la ecuación algebraica de una recta del plano coordenado. Dada una recta del plano, se pueda asociar a la misma una ecuación de la forma ax + by + c = 0, donde a, b y c son números reales (como las rectas que aparecen en la siguiente imagen: x – y – 1 = 0, 3x + 2y – 6 = 0). ¿Cómo funciona la ecuación de la recta? Si tenemos un punto P de coordenadas (x, y), este estará en la recta si los números x e y satisfacen la ecuación, y no estará en ella si no la cumplen. Por ejemplo, los puntos (4, 3), (3, 2) y (0, –1) están en la recta x – y – 1 = 0, ya que (4) – (3) – 1 = 0, (3) – (2) – 1 = 0 y (0) – (–1) – 1 = 0, mientras que el punto (0, 3), no está en ella, por ser (0) – (3) – 1 = – 4, que no es 0; y de la misma manera, los puntos (0, 3) y (2, 0) está en la recta 3x + 2y – 6 = 0, pero no el punto (3, 2).
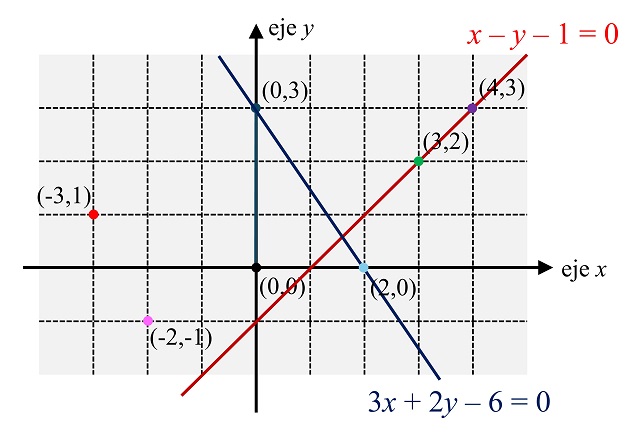
Pero la ecuación de una recta nos da más información. Consideremos de nuevo la recta 3x + 2y – 6 = 0 y veamos que pasa con los puntos que no están sobre ella, como (4, 3), (3, 2), (0, 0) o (–2, –1):
3(4) + 2(3) – 6 = 12, 3(3) + 2(2) – 6 = 7,
3(0) + 2(0) – 6 = –6, 3(–2) + 2(–1) – 6 = –14,
de manera que, en los dos primeros el valor de la ecuación 3x + 2y – 6 es positivo, mientras que en los dos siguientes es negativo.
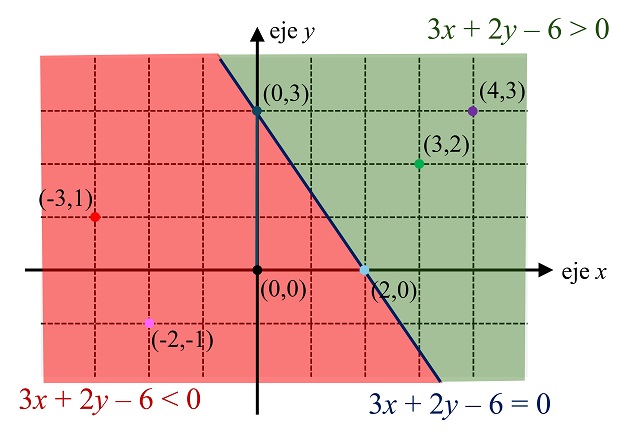
Lo que ocurre es que la ecuación de la recta, en este caso 3x + 2y – 6 = 0, divide al plano en tres regiones distintas, la recta y las dos regiones a cada lado de la misma. Los puntos (x, y) de la recta satisfacen que 3x + 2y – 6 = 0, mientras que los puntos a un lado de la recta satisfacen la desigualdad 3x + 2y – 6 > 0, mientras que los puntos al otro lado de la recta satisfacen que 3x + 2y – 6 < 0. Y esto ocurre en general para cada recta.
Un dispositivo para controlar los marcos
Empecemos recordando que la condición establecida para que los marcos pasen el filtro (o sean considerados pequeños en la fábrica) es que
![]()
siendo x = ancho del marco, y = largo del marco. Pero si miramos la anterior desigualdad desde la óptica de lo visto hasta ahora podemos afirmar lo siguiente.
Consideremos un marco de fotografía concreto, cuyas medidas sean a centímetros de ancho y b centímetros de largo. Este marco se corresponderá, según lo visto, con el punto (a, b) del plano coordenado. Por otra parte, tenemos la ecuación de la recta x + y = 35 (véase la siguiente imagen), dada por las condiciones aplicadas a los marcos fotográficos. Si las coordenadas de nuestro punto (a, b) satisfacen la ecuación la ecuación x + y = 35, entonces el punto está sobre la recta (las medidas del marco a y b satisfacen que a + b = 35, esto es, ancho más largo es igual a 35 centímetros), si verifican que x + y > 35, entonces el punto estará por encima de la recta (las medidas del marco no satisfacen la condición fijada), mientras que si satisfacen que x + y < 35, el punto estará por debajo de la recta (las medidas del marco sí cumplen la condición fijada).
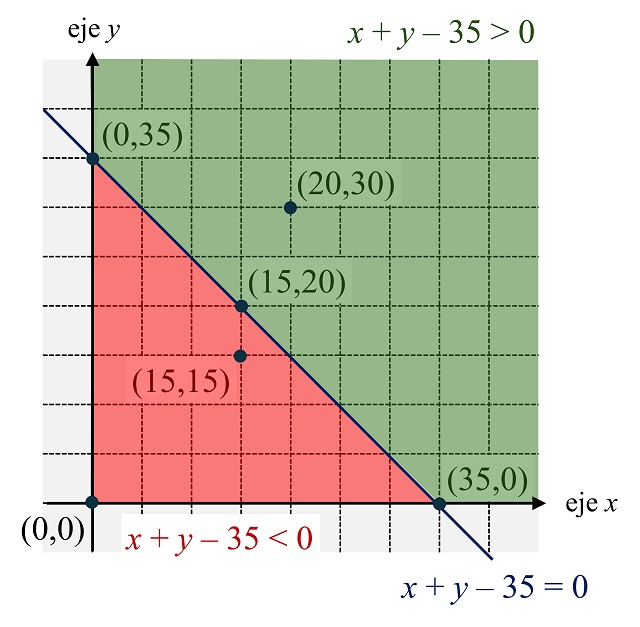
De manera, que podemos observar gráficamente que el marco de medidas (15, 15), es decir, ancho y largo igual a 15 cm, satisface las condiciones establecidas, por estar situado debajo de la recta, así como el marco de medidas (15, 20), que está en la recta, pero no el marco de medidas (20, 30), situado encima de la recta.
En consecuencia, ya tenemos las ideas necesarias para diseñar un dispositivo para controlar que el tamaño de los marcos cumpla esa condición establecida. Este estaría formado por una estructura fija formada por dos lados rectangulares de más de 35 centímetros de largo (una especie de escuadra de dos brazos), junto con una tapa o puerta móvil, unida a la parte vertical de la estructura fija por una bisagra colocada a 35 cm de la base y apoyada en la parte horizontal, a 35 cm de la tabla vertical (utilizando el teorema de Pitágoras sabemos que la tapa tendría una longitud de 35 cm multiplicado por la raíz cuadrada de 2, es decir, unos 49 centímetros).
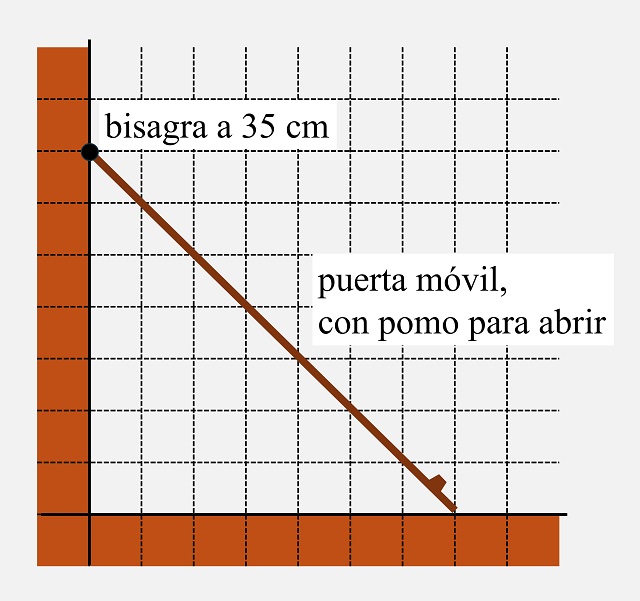
Le he pedido a Gemini que me haga una versión realista del dispositivo. No es que se ajuste del todo a lo que le he pedido, pero quizás con esta imagen os hagáis una mejor idea del mismo, aunque mi idea era un dispositivo apoyado en una superficie plana horizontal, para trabajar mejor con el mismo.

¿Cómo funcionaría el dispositivo? Dado un marco cualquiera, abriríamos la tapa del dispositivo y lo meteríamos dentro apoyándolo en la esquina. Si la tapa cerrase, esto significaría que el marco cumpliría la regla de que la suma de las medidas del marco sea menor, o igual, que 35 centímetros, como en la siguiente imagen.

Mientras que, si la tapa no cerrase, porque lo impide el marco, querría decir que las medidas del marco excederían las que se han fijado en la norma, como se ilustra en la siguiente imagen.

Regreso al dispositivo para controlar las maletas
Una vez entendido el dispositivo bidimensional para controlar las medidas de los marcos de fotografías, o estructuras rectangulares en general, podemos comentar brevemente cual sería el dispositivo para las maletas de mano, o paralelepípedos (cajas rectangulares) en general. La idea es la misma, pero con tres dimensiones, en lugar de dos.
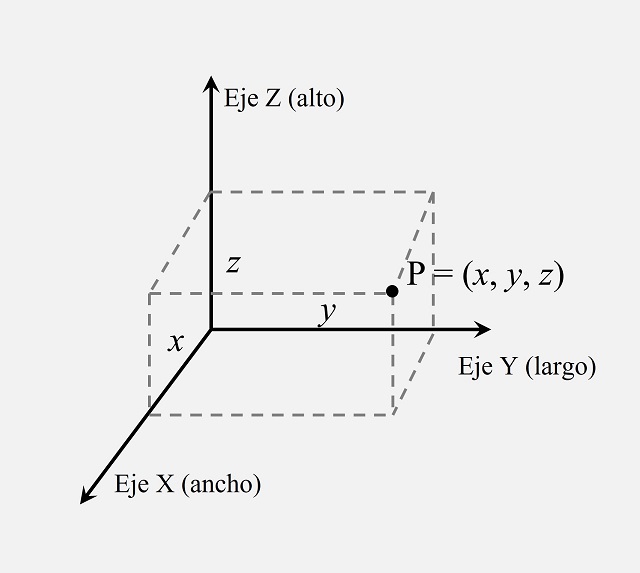
De forma análoga a como ocurría en dimensión dos, ahora las medidas de una maleta / caja rectangular (x, y, z), siendo x el ancho, y el largo y z el alto, determinarán el punto P = (x, y, z) del espacio tridimensional coordenado, que es el vértice opuesto al apoyado en el origen (0,0,0). Y recíprocamente, dado un punto cualquiera del plano P = (x, y, z), este determinará las medidas concretas de una maleta / caja rectangular.
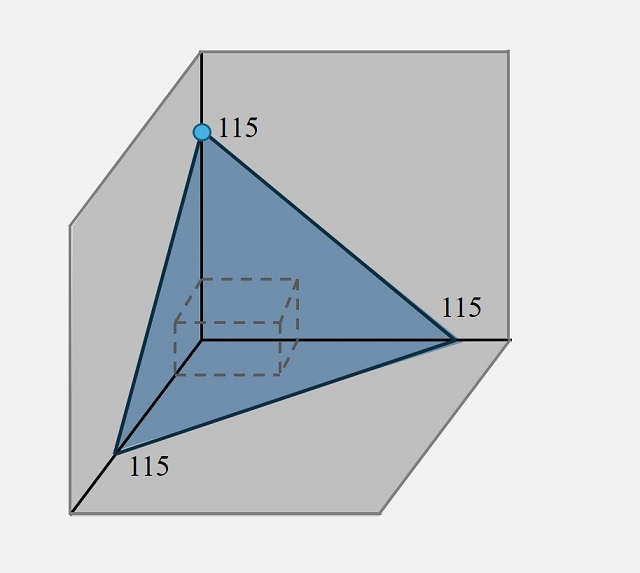
Ahora debemos observar, de manera análoga a lo ocurrido en dimensión dos, que la ecuación x + y + z = 115, derivada de las condiciones generales sobre las maletas, es la ecuación de un plano del espacio tridimensional, que se ilustra en la siguiente imagen. Luego, un punto P = (x, y, z) está en el plano si se cumple la ecuación, estará debajo del plano si x + y + z < 115 y estará por encima del plano si x + y + z > 115.
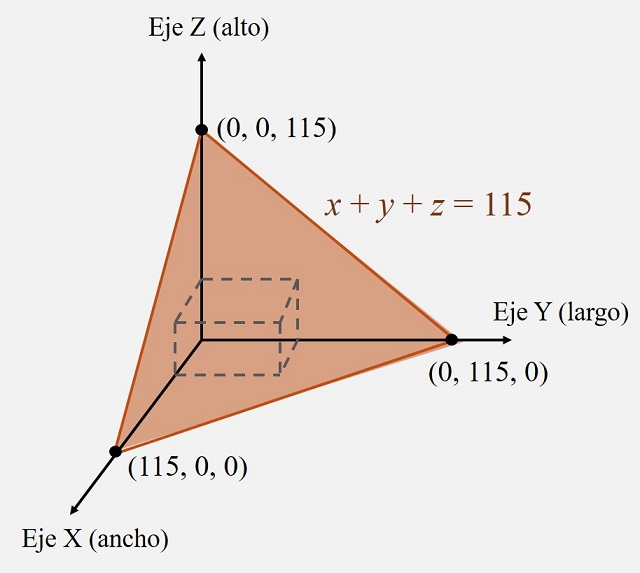
En consecuencia, el dispositivo ahora está muy relacionado con la imagen anterior. Estará formado por tres trozos de planos que se cortan perpendicularmente (en la siguiente imagen las zonas en gris), junto con una tapa triangular cuyos vértices están a 115 cm del vértice origen (de intersección de los tres planos), cuya bisagra estará en el vértice superior para poder abrir esa tapa triangular. El funcionamiento, por lo visto, será igual al de los marcos, si metemos la maleta y se cierra la tapa, estará en las condiciones determinadas (x + y + z menor, o igual, que 115 cm), pero si no cierra la tapa la maleta no puede subirse al avión como equipaje de mano.
Esta era la idea básica con la que se podía haber construido un dispositivo para el control de las maletas de cabina. Por supuesto, con mejoras reales, como mejorar el punto de bisagra. Pero la idea que quería transmitiros es que las matemáticas nos pueden ayudar a aportar soluciones concretas a cuestiones concretas.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica