Para los profanos, la física teórica moderna se puede antojar a veces muy cercana a la ciencia ficción, con continuas referencias a partículas extrañas, energías enormes, máquinas de tamaño kilométrico y, especialmente en gravitación, agujeros negros, de gusano, motores warp y mil y una formas de curvar el espacio y el tiempo en geometrías poco cercanas a la intuición cotidiana.

La realidad es que no sólo la experiencia cotidiana, sino también toda aquella física a la que hemos podido acceder experimentalmente hasta la fecha carece de la presencia de todas estas geometrías tan atractivas para aquellos a los que nos gusta soñar y disfrutamos con la ciencia ficción. Nuestro Universo, el sistema solar, los alrededores de las estrellas, etc… pueden ser descritos con estructuras mucho más sencillas que estas que he nombrado en el párrafo anterior. Por tanto, es razonable preguntarse ¿vale la pena estudiar este tipo de construcciones si no aparecen en la naturaleza? ¿qué sentido tiene que aparezcan como solución de nuestras ecuaciones si no hay ninguna situación física realizable que las contenga? La respuesta a ambas cuestiones reside en la mecánica cuántica y en la forma en que esta funciona.

A día de hoy, y aunque algunos se empeñen en hacer lo contrario y mezclar ciencia y filosofía, la manera apropiada de entender la mecánica cuántica es como una caja cerrada que relaciona situaciones iniciales y situaciones finales a través de unas reglas de cálculo que, en ningún momento, tienen que por qué corresponderse con ninguna realidad física. Como decía David Mermin, lo único que tiene realidad física son los estados finales e iniciales y cómo se correlacionan distintos estados iniciales con distintas situaciones finales. Lo que pase en medio, es una mera herramienta técnica, matemática, una forma de poder trabajar y realizar predicciones que correlacionen estados iniciales y finales.

Así, por ejemplo, para poder calcular cómo se produce la colisión de un electrón y positrón (estado inicial) para producir un par de muones (estado final), utilizamos una entelequia, asumiendo que el paso intermedio se puede descubrir como si las dos partículas iniciales se desintegrasen produciendo un fotón y este a su vez se rompiese en dos para dar el par de muones. Este proceso intermedio es lo que usualmente describimos utilizando diagramas de Feynman.

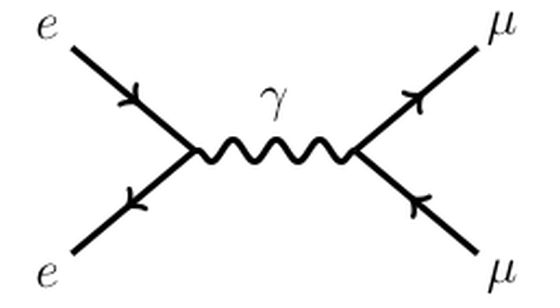
Sin embargo, como acabo de decir, lo que ocurre entre el estado inicial y el final es una mera herramienta para poder realizar un cálculo, una predicción de un valor medible; y no tiene realidad física. Ese fotón intermedio que media entre los dos estados no existe, no es un estado físico y no tiene las propiedades de un fotón normal y corriente.

Lo que Feynman nos enseñó con su interpretación de la mecánica cuántica como suma de historias es que podemos calcular un proceso de este tipo como si entre el inicio y el final se produjesen todas las cosas que se pueden producir (en el ejemplo anterior, creación y desintegración de cualquier partícula propensa a interaccionar con el electrón), con la particularidad de que las restricciones físicas, como limitaciones de energía o de velocidad, no tenían por qué cumplirse. Así, el fotón que se propaga en este diagrama es un fotón, pero no tiene por qué moverse a la velocidad de la luz ni interaccionar exactamente igual que los fotones de la luz que observamos, es una mera herramienta que resulta útil pero no tiene realidad física y a la que los físicos nos referimos como partícula virtual. Es cómoda para los cálculos pero realmente no existe.

Este punto es importante cuando movemos nuestra atención al caso de la gravedad. La Teoría de la Relatividad General, que actualmente es nuestra descripción más sólida de los fenómenos gravitatorios, establece que el objeto fundamental a la hora de describir la interacción gravitatoria es la geometría del espacio y el tiempo. Ambos, juntos en un ente conocido como espacio-tiempo, se comportan como una superficie maleable que se curva bajo la acción de la masa y la energía de los objetos que pueblan el Universo. El objeto fundamental que entendemos como campo gravitatorio es precisamente un objeto matemático que describe cómo es esta geometría en cada punto e instante. La evolución temporal del campo gravitatorio no es más que la forma en que la geometría se deforma con el tiempo.

A este nivel todo está muy claro. La Relatividad General implica unas ecuaciones que relacionan el campo gravitatorio con el contenido de materia y, de esta forma, la materia (y la energía) le dice al espacio cómo curvarse y la curvatura del espacio le dice a la materia cómo moverse pero, ¿cómo se interpreta la gravedad a nivel cuántico? ¿cuál es el papel de la geometría en esta imagen de caja negra de la que hemos hablado antes? La cuestión no es baladí y su respuesta llevó muchos años de trabajo de muchas grandes mentes del siglo XX como Wheeler, Thorne, DeWitt, Veltman, ‘t Hooft, Gibbons o el propio y siempre polémico Stephen Hawking. Precisamente fueron estos dos últimos los que finalmente clarificaron como unificar a nivel formal la descripción de Feynman de la mecánica cuántica con la gravedad, con una teoría que conoce con el nombre de «Euclidean Quantum Gravity».

Basándose en trabajos e ideas previas de Bryce DeWitt, Hawking y Gibbons llegaron a la conclusión de que la aproximación correcta a la hora de fomalizar qué significa una teoría cuántica de la gravedad no tenía por qué ser distina a aquella que durante treinta años (el trabajo de los dos ingleses es de los 70) había tenido un éxito abrumador al describir el resto de las interacciones conocidas en la naturaleza. Así, lo que concluyeron fue que una teoría cuántica de la gravedad no era otra cosa que una forma de relacionar geometrías entre sí, con una caja negra en mitad del proceso que contiene todas aquellas geometrías posibles que interpolen entre la inicial y la final. Tomando un ejemplo práctico, la forma de ver, y predecir valores observables; en un proceso de colapso de agujero negro a nivel cuántico pasaría por sumar sobre todas las posibles geometrías que se puedan conseguir en el camino de deformar un espacio plano (sin gravedad, sin curvatura) a un espacio que no sólo es curvo si no que tiene un agujero (literalmente) en un punto concreto. Y todas estas geometrías intermedias incluyen cosas tan exóticas como que aparezcan otros agujeros que luego se cierren o que crezcan agujeros de gusano conectando zonas lejanas del espacio. Siempre que al final, tras el proceso, la geometría final sea un agujero negro, hay que contar todas las posibilidades intermedias.

Y esta es una de las principales razones de que las geometrías exóticas, particularmente los agujeros de gusano, atrayesen tantísima atención durante los 70 y 80. En principio, uno tiene que considerarlos como estados posibles, aunque no físicos, a la hora de estudiar la transición de una geometría a otra.

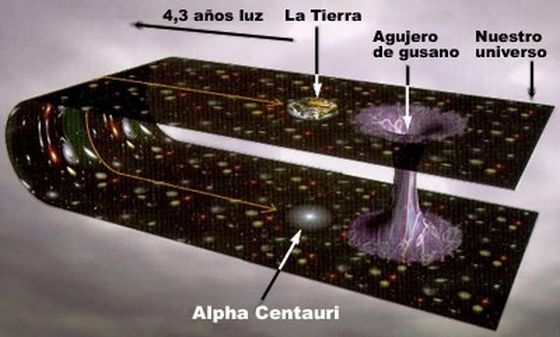
Como perla final, pensemos en un proceso que lleva de un espacio plano, sin gravedad, como la superficie de la Tierra a otro espacio plano (Sí, en la Tierra hay gravedad, pero muy débil comparada con cualquiera de las otras interacciones fundamentales, pensad que un imán de nevera puede vencer a todo un planeta), es decir, la estabilidad del entorno que nos rodea. Si esta imagen de Hawking y Gibbons es cierta, la probabilidad de que esta geometría plana sea estable se calcularía como aquí acabo de describir, sumando sobre todas las geometrías distintas que interpolen entre dos planas. Y esto incluye agujeros negros, de gusano, burbujas Warp, etc… Si lo pensáis, a nuestro alrededor están continuamente apareciendo y despareciendo, en tiempos menores que un instante, todos esos objetos exóticos con los que la ciencia ficción sueña cada día, indetectbles para nosotros pero rodeándonos continuamente.

Realmente, y parafraseando a Neil DeGrasse Tyson en la nueva versión de Cosmos, “La realidad es más increible de lo que jamás podamos imaginar”.

Este post ha sido realizado por Mario Herrero-Valea (@Fooly_Cooly) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.