Galileo (V): los experimentos con bolas y planos inclinados
Los experimentos de caída de bolas por planos inclinados han pasado a la historia de la ciencia por un doble motivo. Por un lado, porque mediante ellos Galileo demuestra que los cuerpos caen con una aceleración constante; o, en la forma en que él lo expresó, que cuerpos ideales -sobre los que no actúan fuerzas de rozamiento ni ningún otro factor que interfiera en la caída- recorrerán al caer una distancia que aumenta con el cuadrado del tiempo transcurrido. Esos resultados sirvieron para establecer la mecánica como una ciencia y prepararon el camino para que Newton, unas décadas después, enunciara las leyes de la mecánica y de la gravitación universal. El segundo motivo es que dio carta de naturaleza al experimento y la expresión matemática de los resultados como método de obtención de conocimiento. Experimentos se habían hecho ya antes, también en la Edad Media, contrariamente a lo que mucha gente piensa, pero lo que no se había hecho era expresar los resultados en términos matemáticos, permitiendo de ese modo incorporar un lenguaje objetivo y universal como vehículo de expresión de los hechos científicos.
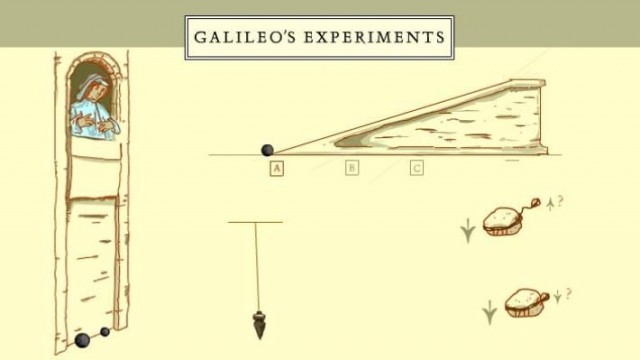
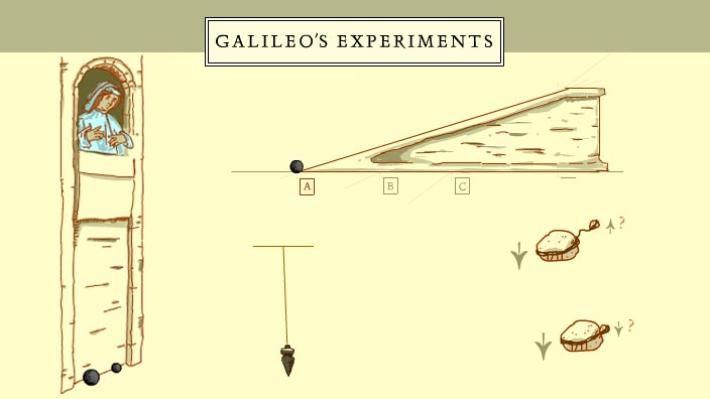
El problema que había en relación con la caída libre es que la velocidad de caída aumenta muy rápidamente, y si no se cuenta con instrumentos de gran precisión, no es posible medir debidamente el tiempo que tarda el cuerpo que cae en cubrir diferentes distancias. Por esa razón, Galileo buscó un método alternativo y pensó que debía “diluir” el efecto de la gravedad. Para eso se le ocurrió utilizar planos inclinados por los que echaba a rodar bolas y medir el tiempo que tardaba en recorrer ciertas distancias. Los planos con la mínima inclinación son los que permiten mediciones más precisas, ya que son los que más “diluyen” el efecto de la gravedad y propician una velocidad de caída más lenta, siempre, claro está, que se minimice el rozamiento o el efecto de cualquier otro factor que pueda interferir. Pero para poderlo hacer, debía estar seguro de que la caída por planos inclinados tiene propiedades equivalentes a la caída libre, aunque se haya “diluido” el efecto de la gravedad.
Argumentó que la velocidad que adquiere un cuerpo rodando por un plano inclinado no depende de la inclinación del plano, sino de la altura que salva el cuerpo que se deja caer. La idea la extrajo de un experimento con un péndulo al que se añade un clavo en una posición intermedia entre el punto del que pende el hilo y el punto más bajo de la trayectoria del cuerpo que se desplaza (en su caso, una bala de plomo). Al dejarla caer desde el punto de partida, la trayectoria de la bala se altera al llegar el hilo a la posición vertical (y la bala al punto más bajo de la trayectoria), pues en ese momento, el clavo colocado bajo el punto del que pende el hilo se interpone en la trayectoria de éste y obliga a que pivote sobre él, reduciéndose así la longitud del péndulo. Sin embargo, la bala llega a una altura que es la misma que la del punto desde el que partió y, a continuación, reinicia su movimiento pendular retornando al punto de partida, esto es, cuando el péndulo recupera sus condiciones iniciales. La observación crucial aquí es que la velocidad a la que pasa la bola por el punto más bajo de su trayectoria es la misma en las dos direcciones, dado que en ambas alcanza después la misma altura. Esto es, la velocidad con la que llega a ese punto más bajo no varía con la longitud del péndulo, sino con la altura que salva al bajar.
A partir de esa observación, Galileo argumenta que si una bola rueda por un plano inclinado hacia abajo y, a continuación, prosigue su movimiento por otro plano inclinado hacia arriba, la bola alcanzará en su trayectoria la misma altura que la del punto del que partió, de forma similar a como ocurre con el péndulo. Y a semejanza del péndulo truncado, da igual que la pendiente de subida sea más alta o más baja; eso sólo hará variar el cambio en la velocidad (que siempre es máxima en el punto inferior), pero no la altura que salva, que dependerá de la velocidad con que inicia la subida.
Si se ignoran las sucesivas pérdidas de impulso debidas al rozamiento, está claro que en ambas direcciones la bola pasa a la misma velocidad por el punto más bajo de su trayectoria, igual que ocurre en el péndulo, con independencia de cuál sea la pendiente del plano. Así, puede imaginarse un plano cada vez más y más inclinado -con una pendiente cada vez mayor- y la bola siempre llegaría al punto más bajo a la misma velocidad. Pues bien, esa inclinación del plano llevado al extremo consistiría en dejar caer la bola en caída libre: también llegaría la bola al punto más bajo a la misma velocidad.
A partir de esa conclusión ya podía hacer los experimentos en los que medir el tiempo que tardaba una bola en recorrer diferentes distancias. De esa forma estableció la ecuación d = ½ g t2, en la que d es la distancia recorrida por la bola, t es el tiempo que tarda en recorrer esa distancia y g el valor de la aceleración debida a la gravedad, que depende de la inclinación del plano, siendo máxima cuando la caída es libre o, lo que es equivalente, cuando el plano es perpendicular a la superficie de la tierra.
Lo paradójico de estos experimentos es que se han suscitado curiosas dudas sobre ellos. El historiador de la ciencia Alexandre Koyré puso en duda que fueran experimentos reales, pues no creía que los medios con los que contaba Galileo para medir el tiempo fueran tan precisos como para arrojar unos resultados que permitieran obtener la ecuación anterior. Según él es muy posible que Galileo llegase a esa ecuación de forma deductiva y los experimentos, que habrían dado resultados sólo aproximados, tendrían valor meramente ilustrativo o, a lo sumo, habrían servido para verificar que la deducción era básicamente correcta. Peter Dear (1995), por su parte, ha escrito que Galileo no describió ningún experimento ni registró los resultados de forma detallada, sino que se limitó a decir que utilizando un dispositivo determinado, descubrió que los resultados concordaban exactamente con sus supuestos teóricos (dice que repitió las pruebas “cien veces”). Un poco más arriba había escrito que los había hecho “a menudo”, lo que, según Dear, son formas de decir “tantas veces como queráis”. A la hora de valorar estas opiniones más o menos escépticas, conviene recordar también que la deducción de Galileo no es del todo original, sino deudora de la demostración geométrica realizada por Oresme (1323-1382) del llamado Teorema de Merton de la velocidad media (demostrado a su vez en forma algebraica por William de Heytesbury en 1335).
A pesar de las dudas, también ha habido autores que han reproducido los experimentos de la forma en que los describió Galileo y han obtenido resultados precisos y acordes con las expectativas. En todo caso, de lo que no cabe duda es de que Galileo abrió un camino para la ciencia que es el que se ha seguido desde entonces y se ha consolidado como parte esencial de la misma práctica científica. Y este experimento de las bolas resulta, incluso si sólo llegó a ser un experimento mental, desde ese punto de vista, modélico.
Bibliografía consultada
Peter Dear (1995): Discipline and Experience: The Mathematical Way in the Scientific Revolution The University of Chicago Press
Maurice A. Finocchiaro (2008): The essential Galileo Hackett Publishing Co
John Gribbin (2003): Historia de la ciencia 1543-2001 Crítica (Science. A History, 1543-2001, 2002, Allen Lane)
Javier Ordóñez, Víctor Navarro y José Manuel Sánchez Ron (2003): Historia de la Ciencia Espasa Calpe (el capítulo Edad Moderna es de Víctor Navarro)
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología en la UPV/EHU y coordinador de la Cátedra de Cultura Científica de esta universidad.
Galileo (VI): errores | General | Cuaderno de Cultura Científica
[…] (V) Los experimentos con bolas y planos inclinados […]
Galileo (y VII): recapitulación | General | Cuaderno de Cultura Científica
[…] (V) Los experimentos con bolas y planos inclinados […]
Galileo (II): aportaciones | General | Cuaderno de Cultura Científica
[…] (V) Los experimentos con bolas y planos inclinados […]
Galileo (I): el personaje | Series | Cuaderno de Cultura Científica
[…] (V) Los experimentos con bolas y planos inclinados […]