Esta tarde mientras estaba frente a mi ordenador pensando en el tema de mi siguiente entrada del Cuaderno de Cultura Científica, el termómetro en el exterior de la casa donde estoy pasando unos días marcaba más de 35 grados centígrados. ¿De qué tema se puede escribir con un calor como este, que además será similar al que soporten las personas que después van a leer esta entrada?
Después de darle varias vueltas, me decidí por las propiedades “mágicas” del número nueve, un tema que podríamos incluir dentro de los más refrescantes para el calor del verano. Eso sí, dejé su escritura para la noche, que es más fresca,… y aquí estamos.
En realidad de todos los números podemos mostrar curiosas propiedades y anécdotas, aunque el número 9 tiene algunas particularidades que ya quedan en evidencia en los ejemplos de esta entrada.

Para empezar, veamos las curiosas torres de potencias, cuadradas y cúbicas, de números formados solo por nueves, que generalizan las igualdades 92 = 81 y 93 = 729.
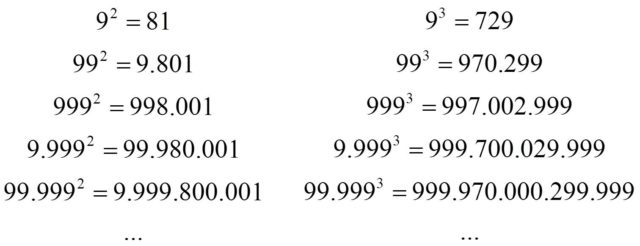
Como vemos los resultados se pueden obtener de una forma mecánica. En el caso del cuadrado, a partir de las expresión inicial 92 = 81, por cada 9 que se añade en la parte de la izquierda para elevar al cuadrado, se van añadiendo, en la parte de la derecha, un 9 al principio del número anterior y un 0 después del 8. Con el cubo pasa algo similar, como podéis observar.
Otras dos sorprendentes torres aritméticas relacionadas con el número 9 son las siguientes. La primera, la multiplicación del número 987.654.321 por los múltiplos del 9, es una consecuencia directa de la tabla de multiplicar del número 9.
 La otra torre es de nuevo una serie de multiplicaciones por los múltiplos de 9, pero esta vez se multiplican por el número 12.345.679.
La otra torre es de nuevo una serie de multiplicaciones por los múltiplos de 9, pero esta vez se multiplican por el número 12.345.679.
 Los resultados de esta torre se deben a que el número 12.345.679 se puede expresar como (109 – 1)/81, por lo que al multiplicarlo por potencias de 9, es decir, 9N (para N tomando los valores 1, 2, 3, …, 8, 9), se obtiene
Los resultados de esta torre se deben a que el número 12.345.679 se puede expresar como (109 – 1)/81, por lo que al multiplicarlo por potencias de 9, es decir, 9N (para N tomando los valores 1, 2, 3, …, 8, 9), se obtiene
Algunas de las propiedades mágicas de este número están basadas en la regla de divisibilidad del nueve. Recordemos que esta regla nos dice que un número es divisible por 9 si la suma de los dígitos que lo componen también es divisible por 9. Así, el número 3.401.073 es divisible por 9 puesto que la suma de sus dígitos 3 + 4 + 0 + 1 + 0 + 7 + 3 = 18 es divisible por 9, mientras que 5.367.032 no lo es puesto que 5 + 3 + 6 + 7 + 0 + 3 + 2 = 26 tampoco lo es. Además, esta propiedad se puede utilizar de forma recursiva, por ejemplo, el número 3.479.388.345.659 será divisible por 9 si lo es la suma de sus dígitos, 3 + 4 + 7 + 9 + 3 + 8 + 8 + 3 + 4 + 5 + 6 + 5 + 9 = 74, que sabemos que no es divisible por 9 puesto que 7 + 4 = 11 no es un número divisible por 9, luego tampoco el primer número.
Una aplicación de esta regla es un sencillo, pero muy efectivo, truco de magia que en su día me enseñó mi compañero Pedro Alegría y que explicamos en uno de los videos de la sección “Una de mates” del programa de televisión, dirigido por José A. Pérez, Órbita Laika, en su segunda temporada. El truco se basa en la regla de divisibilidad del 9, y más concretamente, en el hecho de que si conocemos todos los dígitos, salvo uno, que componen un número divisible por 9, podemos averiguar el dígito desconocido fácilmente. Por ejemplo, si el número 657.A43 es divisible por 9, entonces 6 + 5 + 7 + A + 4 + 3 = 25 + A debe ser divisible por 9, pero el siguiente número divisible por 9 después del 25 es el 27, de donde se deduce que A = 2.
Albert Beiler, en su libro Recreations in the Theory of Numbers, presenta el siguiente reto que apareció en su día en la parte de los juegos y crucigramas de una revista. Se trataba de averiguar, en sesenta segundos, el valor de A para que se diera la siguiente igualdad, 2.A99.561 = [3 (523+A)]2. Este es un rompecabezas que da la impresión de ser imposible de resolver en 60 segundos, salvo que nos percatemos que la parte de la derecha es un múltiplo de 32 = 9. Así, utilizando la regla de divisibilidad del 9 y el hecho de que 2 + 9 + 9 + 5 + 6 +1 = 32, se deduce fácilmente que el valor de A es 4, ya que el siguiente múltiplo de 9 es 36.
Antes de explicar el truco de magia para que quienes quieran lo puedan realizar en su entorno familiar o de amigos, o incluso explicarlo en clase si son docentes (es una buena herramienta para que los estudiantes aprendan las reglas de divisibilidad), puede verse el video “Magia matemática” de Órbita Laika.
Para realizar el truco se necesita una persona con una calculadora. Se le pide que multiplique, sin que el mago lo vea, diez o doce números en la calculadora. Mientras multiplica los números se le puede recordar que elija los números al azar, utilizando todo el teclado numérico, pero que no multiplique por 0, ya que la multiplicación daría 0, o por 1, que deja la multiplicación igual.
Por ejemplo, dicha persona podría realizar la multiplicación 5 x 6 x 3 x 4 x 2 x 9 x 7 x 3 x 9 x 8 x 7 x 6 = 411.505.920, mientras que la persona que realiza el truco no habría visto los números que se han multiplicado, ni el resultado de dicha multiplicación.
Aunque esto no es propiamente el truco, que es de adivinación, el mago puede empezar por comentar que intuye, o alguna expresión similar, que el número fruto de la multiplicación termina en 0. Esto se debe a que seguramente entre los números multiplicados estará el número 5 y algún número par, por lo que la multiplicación es múltiplo de 10, y el resultado termina en 0.
Y ahora es cuando empieza la parte de la adivinación. Se le pide a la persona que elija uno de los dígitos del número que ha salido en la multiplicación y que tiene escrito en la pantalla de la calculadora, que no sea un 0, que lo guarde en su cabeza y que diga en alto los demás dígitos del número, en el orden que quiera. El mago adivinará, utilizando la regla de divisibilidad del 9, el dígito que falta, el elegido por la persona y que no ha sido dicho en alto. Se puede hacer uso de la regla de divisibilidad del 9 porque el número obtenido de la multiplicación es, con mucha probabilidad, múltiplo de 9, ya sea porque uno de los números elegidos es directamente el 9, porque haya dos 3s o dos 6s en la multiplicación, o porque haya, al menos, un 3 y un 6.
Veámoslo con el ejemplo anterior, la multiplicación 5 x 6 x 3 x 4 x 2 x 9 x 7 x 3 x 9 x 8 x 7 x 6 = 411.505.920. Supongamos que la persona a la que se le hace el truco ha elegido un 5, y que el resto de los dígitos los dice en el siguiente orden: 0, 2, 9, 0, 5, 1, 1 y 4.
¿Cómo adivinar el dígito desconocido? Fácil. Sumamos el resto de dígitos, 0 + 2 + 9 + 0 + 5 + 1 + 1 + 4 = 22, y como el siguiente múltiplo de 9 es el 27, el dígito que falta es efectivamente el 5.
Una vez visto este sencillo truco de magia, revisemos la regla de divisibilidad del 9. Esta se debe a que utilizamos un sistema de numeración posicional en base 10, luego que se apoya en las potencias de 10. Así, el número que representamos como 68.735 tiene el valor
6 x 10.000 + 8 x 1.000 + 7 x 100 + 3 x 10 + 5.
Y 9 es igual a 10 – 1. Además, que un número sea divisible por 9 es lo mismo que el resto de la división por 9 sea 0. Por lo tanto, para comprender la regla de divisibilidad del 9 tenemos que analizar cómo es el resto de la división de un número cualquiera por 9 (o lo que es lo mismo, saber si el número es congruente con 0, módulo 9).
Como la base de nuestro sistema de numeración es el 10, lo primero que observamos es que el resto de dividir 10 por 9 es 1. Y lo mismo ocurre para las potencias de 10, 10n dividido por 9 es igual al número formado por n unos y el resto de la división es 1. Luego dado un número a (entre 0 y 9), el resto de dividir el número (a 10n) por 9 es a.
En conclusión, dado un número genérico
,
como el resto de dividir cada uno de los sumando de N, , por 9, es igual a
, se tiene que el resto de dividir N por 9 es igual al resto de dividir la suma de los coeficientes
por 9, de lo cual se deriva que el resto de dividir un número por 9 es igual al resto de dividir la suma de sus dígitos por 9, y en particular, la regla de divisibilidad del 9.
Veamos un ejemplo. Si dividimos 68.735 por 9 se obtiene como resultado 7.637 y de resto 2. Si lo hacemos sumando a sumando en su expresión decimal, 60.000 dividido 9 tiene como resto 6, 8.000 tiene como resto 8, 700 tiene 7, 3 tiene 30 y luego el 5, luego sumando los restos (que son los dígitos del número) tenemos 29, cuyo resto al dividirlo por 9 es también 2.
Esta propiedad se utiliza también como regla para comprobar si las operaciones aritméticas están bien hechas, la conocida prueba del 9. Por ejemplo, los contables la utilizaban, en los tiempos anteriores al ordenador, para comprobar las grandes sumas, puesto que el resto de dividir por 9 el resultado de una suma debe ser igual al resto de la suma de los restos de los sumandos.
Veamos un ejemplo…
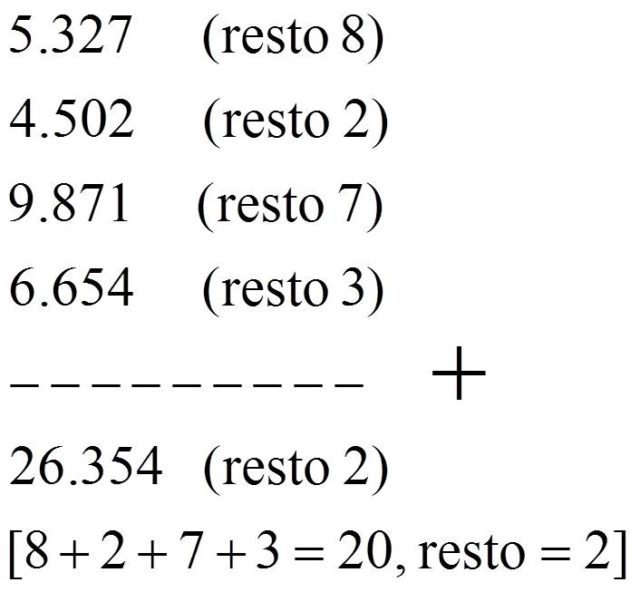
Evidentemente, ya que 5.327 + 4.502 + 9.871 + 6.654 = (591 x 9 + 8) + (500 x 9 + 2) + (1.096 x 9 + 7) + (739 x 9 + 3) = 2.926 x 9 + 20 = 2.928 x 9 + 2 = 26.354.
Podemos ver otro ejemplo con la multiplicación. El resto de dividir por 9 el producto de dos números es igual al resto del producto de los restos de los números multiplicados.

Y de nuevo, es fácil comprobarlo, puesto que 4.358 = 484 x 9 + 2 y 292 = 76 x 9 + 8.
Según Thomas Heath, en su libro A History of Greek Mathematics, vol I: From Thales to Euclid (1921), la prueba del 9 ya era conocida en la Grecia Clásica. Aparece descrita en la obra “Refutatio omnium haeresium” (Refutación de todas las herejías) del obispo Hipólito de Roma (170-235) y también en el comentario del filósofo neoplatónico Jámblico (aprox. 245-325) de la “Arithmetike eisagoge” (Introducción a la aritmética) del matemático Nicómaco de Gerasa (aprox. 60-120).
Terminaremos con otras dos torres aritméticas similares a las anteriores, que al igual que las anteriores aparecen en el libro Recreaciones Matemáticas de Édouard Lucas.

La explicación de esta torre aritmética es la siguiente. La parte de la izquierda de las igualdades se puede expresar de la siguiente forma en función de las potencias de 10,
,
y si realizamos la multiplicación y simplificamos se obtiene
,
es decir, exactamente n+1 unos, la parte de la derecha de las igualdades.
Y la última torre, similar a la anterior.

De nuevo, podemos comprobarla. La parte de la derecha puede escribirse, en base 10, de la siguiente forma
,
y si realizamos la multiplicación y simplificamos se obtiene
,
es decir,
.
Y haciendo uso de la fórmula
,
se obtiene la expresion
,
la cual, utilizando de nuevo la fórmula anterior, se convierte en
,
es decir, 8 multiplicado por el número formado por (n + 1) unos, como denota la expresión de la derecha de la torre.

Bueno, hemos terminado el artículo a una temperatura agradable… ahora a continuar disfrutando de la noche, espero que vosotros hayáis disfrutado de esta entrada.
Bibliografía
1.- Video “Magia matemática” de la segunda temporada del programa de televisión Órbita Laika (director: José A. Pérez Ledo), de la sección “Una de mates” (guión y presentación de Raúl Ibáñez), 2015.
2.- Albert Beiler, Recreations in the Theory of Numbers, Dover, 1964.
4.- Graham Flegg, Numbers, Their History and Meaning, Dover, 1983.
5.- Thomas Heat, A History of Greek Mathematics, vol I: From Thales to Euclid, Oxford University Press, 1921.
6.- Éduoard Lucas, E., Recreaciones matemáticas, vol. 1 – 4, Nivola, 2007 y 2008.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Hitos en la red #130 – Naukas
[…] o se te hacen eternas las noches de invierno (si estás en el Sur)? Échale cabeza, papel y lápiz: El número nueve en una noche de verano por Raúl Ibáñez; o, simplemente, lee: El caso del “Solitario” George de Eduardo Angulo, […]
Hitos en la red #130 | Para Entretener
[…] o se te hacen eternas las noches de invierno (si estás en el Sur)? Échale cabeza, papel y lápiz: El número nueve en una noche de verano por Raúl Ibáñez; o, simplemente, lee: El caso del “Solitario” George de Eduardo Angulo, […]
Las emocionantes aventuras del número tres (I) — Cuaderno de Cultura Científica
[…] Hace pocos días que hemos entrado en el verano, las clases ya han finalizado y los exámenes –salvo la convocatoria extraordinaria– también, incluidos los exámenes de selectividad con sus continuas polémicas. Esto quiere decir que algunas personas ya están de vacaciones y es tiempo de lecturas tranquilas y sugerentes. Por este motivo, voy a dedicar una serie de entradas del Cuaderno de Cultura Científica a hablar de algunas cuestiones matemáticas y culturales del número tres, como ya hice en relación a los números siete y nueve en el verano de 2016 (en las entradas El número siete, un número muy popular y El número nueve en una noche de verano). […]