“Cuatro peces exóticos, iluminados por una luz blanca de neón, daban vueltas en un enorme acuario situado justo en medio de la habitación. Una tabla, colocada sobre dos caballetes, se combaba bajo el peso de libros que trataban de matemáticas puras. Hojas garabateadas con ecuaciones y cálculos tenebrosos los recubrían. Otras estaban esparcidas por el suelo, algunas arrugadas. En un rincón había una bolsa de deporte con la efigie de los Foreurs de Val-d’Or. Encima había tres bastones de hockey. Bastones de zurdo con la pala muy curvada; sin duda de un delantero.

Al otro lado de la calle se entreabrió una puerta. En el rellano del piso de la planta baja apareció Julie, todavía vestida con aquella bata tan corta. Con desdén, tiró en el contenedor azul la botella de vino vacía, que se rompió al primer golpe. El hombre salió deprisa, mirando a derecha e izquierda. Hizo un pequeño gesto con la mano a Julie, que no le contestó. Cerró con un tremendo portazo. Su historia de amor había terminado.

Boris Bogdanov interrumpió la lectura de un libro de Andrei Markov, no el jugador de hockey sino el gran matemático ruso. Desde su ventana lo había visto todo. Boris Bogdanov esbozó una sonrisita enigmática, como si supiera algo que su vecina ignoraba.

¿Acaso Boris Bogdanov estaba enamorado de la vecina?

Niet! Boris Bogdanov no se había enamorado nunca, pues lo único que le interesaba desde siempre era su propia persona y sus peces.”

Este fragmento pertenece a las primeras páginas de la novela “El frío modifica la trayectoria de los peces” (2009) del escritor canadiense Pierre Szalowski. Entre los personajes de esta novela coral nos encontramos al ruso Boris Bogdanov, que es matemático, bueno más concretamente topólogo.

El tema de la tesis doctoral de este matemático ruso afincado en Montreal (Canadá), que está relacionada con la trayectoria que describen los peces mientras nadan, es una metáfora de la historia que cuenta esta tierna y singular novela. En esencia que la trayectoria de las personas, es decir, su vida, se ve afectada por la trayectoria de las demás personas, y cuando nuevas personas aparecen en la vida de alguien, su trayectoria, es decir, su vida, puede cambiar, en el caso de la novela para mejorarla.

El matemático ruso Boris Bogdanov está realizando su tesis doctoral en una rama de las matemáticas que se llama topología, es decir, es un topólogo. ¿Qué significa esto? Según un viejo chiste matemático, un topólogo es una persona que no conoce la diferencia entre un donuts y una taza de café.

La topología es una rama de las matemáticas que estudia los objetos geométricos sin tener en cuenta las cuestiones métricas, es decir, las distancias o las formas, y solamente se preocupa de las relaciones espaciales como la proximidad o la continuidad. Por este motivo, popularmente se suele conocer a la topología como la “geometría de la goma elástica”. Si tomamos una superficie elástica, como por ejemplo una goma, y dos puntos de ella que están separados una distancia de un centímetro, al estirar dicha superficie, esos dos puntos seguirán estando más o menos próximos, en relación al conjunto, aunque la distancia entre ellos se habrá modificado, es decir, cambia su geometría, pero no su topología.

Si se deforma un objeto geométrico, estirando o encogiendo, pero sin cortarlo, ni pegando partes del mismo (esto modificaría la proximidad de sus puntos, por ejemplo, puntos que no estuviesen próximos pasarían a estarlo al pegar dos partes del objetos geométrico, y al contrario si se cortase), no cambia la topología del objeto, es decir, son el mismo objeto topológico, aunque no geométrico. Con unas “gafas topológicas” serían indistinguibles, serían el mismo, aunque no con unas “gafas geométricas”. Por ejemplo, una circunferencia y un cuadrado son geométricamente distintos, al transformar uno en otro no se mantiene la forma, ni las distancias entre sus puntos, pero sí las proximidades, se mantiene la continuidad.

Pero regresemos a la novela “El frío modifica la trayectoria de los peces” y a la presentación que en la misma se hace de la matemática de su personaje ruso.

“Boris Bogdanov era un apasionado de la topología o, mejor dicho, de una de sus disciplinas. La teoría de los nudos es una ciencia matemática compleja que permite explicar cosas muy simples de la vida. Cuando se tira del hilo de un ovillo de lana enmarañada, unas veces se deshace de golpe, otras veces se enreda aún más. Es como la vida: pequeños gestos pueden tener grandes consecuencias. Y a veces el mismo gesto no tiene el mismo efecto.

Los peces exóticos de Boris Bogdanov le permitían reflexionar sobre su nueva teoría. Un pez en un acuario siempre sigue el mismo recorrido, tira de su propio hilo. Lo desenrolla en función de la presencia de los demás peces, amigos o enemigos, en el acuario. Asimismo, debe modificar su camino ritual cuando llega un nuevo inquilino. Para Boris, estos itinerarios eran hilos que se anudaban y se desanudaban.

—Tú no escoges tu camino, los demás lo hacen por ti.

Su tesis de doctorado estaba ahí, ante él, en un agua que mantenía a treinta y dos grados. Aquello era vital. Su supervivencia universitaria dependía de que siguiera a la misma temperatura. Si descendía, algunos peces podrían modificar su camino y echar por tierra toda la teoría defendida en su tesis.

Sus trabajos no habían dejado indiferente al presidente de la Sociedad Matemática de Canadá, con sede en Calgary, en Alberta, donde hace tanto frío.

—Venga a vernos cuando termine con sus peces. ¡Las matemáticas térmicas serán un cambio para nosotros!”

La topología se divide a su vez en varias ramas, entre las que nos encontramos la topología algebraica, la teoría de grafos, o la teoría de nudos. A esta última pertenece la investigación que está realizando el matemático Boris Bogdanov con sus peces. La trayectoria cerrada que realizan los peces, en el acuario de Bogdanov, es un nudo, un nudo matemático.

Un nudo matemático esencialmente es un nudo realizado sobre una cuerda que tiene los extremos pegados y que por lo tanto no se puede desanudar. Por supuesto, matemáticamente nos interesa la línea que describe la cuerda y no el grosor de la misma o su trenzado. Es decir, un nudo matemático es una curva cerrada en el espacio. El nudo más simple es la circunferencia, en la que no existe nudo, podríamos decir que es el no-nudo.

Como estamos hablando de nudos en topología, podemos deformar estirando la línea y cambiándola de forma, lo cual no altera el nudo, siempre que no se corte o pegue. Así, en la siguiente imagen, los dos primeros nudos son el mismo, son el no-nudo. Mientras que el tercer nudo de la imagen ya no es un no-nudo, es el nudo más simple después de este, es el nudo trébol.

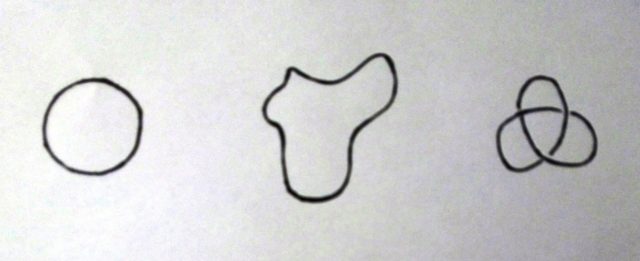
La teoría de nudos estudia cuántos nudos distintos, es decir, topológicamente diferentes, existen, así como propiedades topológicas de los mismos. En particular, se desarrollan herramientas matemáticas para saber si dos nudos aparentemente diferentes son iguales (topológicamente), o no. Por ejemplo, se puede demostrar que el complejo nudo que aparece en la siguiente imagen, y que se conoce como nudo gordiano de Haken, es topológicamente equivalente al no-nudo, es decir, no hay nudo, solamente está enmarañado. Es (topológicamente) el no-nudo.

Los nudos, que son curvas cerradas en el espacio, se suelen representar como un diagrama plano (como en las imágenes anteriores), que sería como dejar caer la cuerda anudada, y cerrada, sobre una mesa, indicando con un trazo discontinuo cuando la línea va por abajo, como se ve en las imágenes anteriores, y en las siguientes. Un mismo nudo puede tener diferentes diagramas planos, y una información importante en el estudio de los nudos es el número de cruce, es decir, el menor número de cruces posibles en todos los diagramas posibles de un nudo. Así en el no-nudo el número de cruce el 0, ya que aunque el diagrama conocido como nudo gordiano de Haken tiene muchísimos cruces, la representación simple, la circunferencia, no tiene ninguno.

El nudo trébol tiene número de cruce 3, de hecho, es el único nudo con número de cruces igual a 3. De igual forma, solo existe un nudo con número de cruce igual a 4, el nudo de Saboya, que podemos ver en la siguiente imagen. Para números de cruce pequeños no existen muchos nudos distintos, pero la cantidad aumenta rápidamente. En la siguiente imagen vemos los 14 nudos con 7 cruces o menos, salvo el no-nudo, mientras que hay 1.388.705 nudos topológicamente diferentes con número de cruce igual a 16.

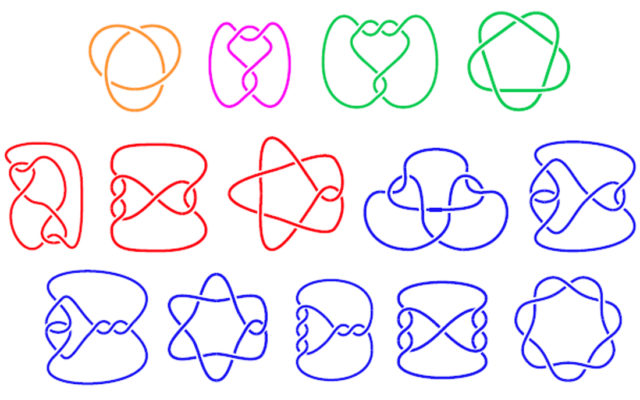
En la siguiente tabla podemos observar cómo crece rápidamente la cantidad de nudos topológicamente diferentes según va creciendo el número de cruces.

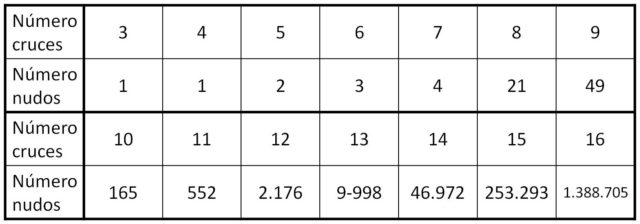
Si pensamos de nuevo en la historia del libro “El frío modifica la trayectoria de los peces” y en el personaje del matemático Boris Bogdanov debemos de reconocer que lo importante es el carácter del ruso, su relación con Julie y en lo que respecta a su investigación matemática, que esta es una metáfora del mensaje que se encierra en la novela, pero no es importante que su investigación no sea, desde una perspectiva matemática, creíble, o cuando menos no queda claro en la novela en qué consiste.

En la novela se cuenta que en su investigación Boris se dedica a mantener su pecera con cuatro peces exóticos a una misma temperatura, 32 grados, y a comprobar que los cuatro peces mantienen las mismas trayectorias cerradas a esa temperatura, trayectorias que como hemos leído en el segundo fragmento dependen las unas de las otras. Y al final de la novela, descubre que el frío modifica la trayectoria de sus peces, pero más aún, con el frío empiezan a nadar en parejas. Solo con esa información parece en realidad una tesis doctoral de ictiología.

No hay nada en la novela que muestre qué tipo de estudio topológico, de teoría de cuerdas, realiza el matemático ruso. Si se trata de una investigación topológica, de teoría de cuerdas, debería estudiar por ejemplo qué tipo de nudos son las trayectorias de los peces o cuáles son sus propiedades topológicas, aunque no hay ninguna evidencia de que así sea. Aunque qué más da, supongamos que realmente eso es lo que está haciendo, o algo similar, pero que en la novela no es relevante contarlo.

Eso sí, las pocas matemáticas que realiza Boris y que aparecen mencionadas son realmente cálculos, como se ve en este fragmento.

“Boris Bogdanov […] cogió del suelo la primera hoja que vio. Por la parte de delante estaba llena de cálculos. Le dio la vuelta, estaba en blanco. Cogió del escritorio una regla milimetrada y un lápiz. Rápidamente dibujó una vista isométrica del acuario. Midió el formato exacto. Con algunos cálculos sacó el volumen. Para Boris Bogdanov, aquel tipo de cálculos era a la aritmética lo que la apertura de piernas para una bailarina: rutina.

A continuación Boris Bogdanov se lanzó a realizar cálculos térmicos. En una tabla que trazó rápidamente anotó con cuidado el tiempo que el acuario tardaría en enfriarse, considerando la temperatura ambiente.

Pudo definir un algoritmo que determinaba la cantidad de agua caliente que debería añadir en el acuario en caso de que la temperatura bajase. Si sacaba un litro de agua a treinta y un grados, tendría que añadir cuatrocientos cincuenta y nueve mililitros de agua a noventa y ocho grados para que la totalidad del acuario recuperara los treinta y dos grados. Continuó con sus cálculos, incluyendo diversas presiones atmosféricas posibles, si el agua caía a veintinueve, veintiocho, veintisiete, veintiséis, veinticinco, veinticuatro, veintitrés y veintidós grados. No se atrevió a contemplar la posibilidad de una temperatura más baja.”

Para terminar, el autor de la novela, Pierre Szalowski, quiere transmitir que la tesis topológica del matemático ruso fue una gran tesis doctoral que le convirtió en un excepcional matemático, como podemos leer hacia el final del libro.

“Boris había cambiado mucho desde que era doctor en matemáticas en la Universidad McGill. Eminencia mundial en topología, publicaba regularmente el resultado de sus trabajos en la revista Nature, la referencia mundial. Cuando recibió la medalla Fields, recompensa suprema del matemático, tuvo la convicción de que pasaba a formar parte de la dinastía de los grandes investigadores del eximperio soviético y que se unía a sus héroes de infancia, glorias del régimen comunista, cuyos pasos había querido seguir.”

Bibliografía

1.- Pierre Szalowski, El frío modifica la trayectoria de los peces, Grijalbo, 2009.

2.- María Teresa Lozano, La teoría de nudos en el siglo XX, Un paseo por la Geometría 1998/99, UPV-EHU, 1999. [Versión on-line en www.divulgamat.net]

3.- Ian Stewart, La cuadratura del cuadrado, Crítica, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica