El ritual de los Musgrave –recogido en Memorias de Sherlock Holmes– es un relato corto deArthur Conan Doyle en el que aparecenel famoso detective y la familia Musgrave, una de más antiguas de Inglaterra.

En este relato corto, Reginald Musgrave –un compañero de colegio de Sherlock Holmes– contrata al detective para que investigue la desaparición de Richard Brunton –el mayordomo– y de Rachel Howells –la segunda doncella–.

Musgrave ha encontrado unos días antes al mayordomo fisgando unos papeles en la biblioteca y le ha despedido, dándole el plazo de una semana para irse de la casa. Pero Brunton desaparece y poco más tarde la doncella enamorada del mayordomo, que la ha abandonado por otra.

El papel que el mayordomo leía en la biblioteca era el Ritual de los Musgrave:

“– ¿De quién era?

– Del que se ha marchado.

– ¿Quién la tendrá?

– El que vendrá.

– ¿Dónde estaba el sol?

– Sobre el roble.

– ¿Dónde estaba la sombra?

– Bajo el olmo.

– ¿Con qué pasos se medía?

– Al norte por diez y por diez, al este por cinco y por cinco, al sur por dos y por dos, al oeste por uno y por uno, y por debajo.

– ¿Qué daremos por ella?

– Todo lo que poseemos.

– ¿Por qué deberíamos darlo?

– Para responder a la confianza.”

El detective –con gran acierto– piensa que en el ritual debe estar la clave del misterio, y que Brunton –un hombre inteligente– debía haberse empeñado en encontrar el secreto escondido entre aquellas extrañas palabras:

“Fue perfectamente obvio para mí, al leer el Ritual de los Musgrave, que las medidas habían de referirse sin duda a algún punto al que aludía el resto del documento, y que si podíamos encontrar ese punto estaríamos en buen camino para saber cuál era aquel secreto que los antiguos Musgrave habían juzgado necesario enmascarar de un modo tan curioso y peculiar. Para comenzar se nos daban dos guías: un roble y un olmo. En cuanto al roble, no podía haber la menor duda. Directamente ante la casa, a la izquierda del camino que llevaba a la misma, se alzaba un patriarca entre los robles, uno de los árboles más magníficos que yo haya visto jamás.

– ¿Ya estaba aquí cuando se redactó vuestro Ritual? –pregunté al pasar delante de él.

– Según todas las probabilidades, ya lo estaba cuando se produjo la conquista normanda –me respondió–. Tiene una circunferencia de veintitrés pies.

Así quedaba asegurado uno de mis puntos de partida.

– ¿Tenéis algún olmo viejo? –inquirí.

– Antes había uno muy viejo, pero hace diez años cayó sobre él un rayo y sólo quedó el tocón.

– ¿Puedes enseñarme dónde estaba?

– Ya lo creo.

– ¿Y no hay más olmos?

– Viejos no, pero abundan las hayas.

– Me gustaría ver dónde crecía.

Habíamos llegado en un dog-cart, y mi cliente me condujo en seguida, sin entrar en la casa, a una cicatriz en la hierba que marcaba donde se había alzado el olmo. Estaba casi a mitad de camino entre el roble y la casa. Mi investigación parecía progresar.

– Supongo que es imposible averiguar qué altura tenía el olmo –quise saber.

– Puedo decírtelo en seguida. Medía sesenta y cuatro pies.

– ¿Cómo lo sabes? –pregunté sorprendido.

– Cuando mi viejo profesor me planteaba un problema de trigonometría, siempre consistía en una medición de alturas. Cuando era un mozalbete calculé las de todos los árboles y edificios de la propiedad. Había sido un inesperado golpe de suerte y mis datos acudían a mí con mayor rapidez de la que yo hubiera podido esperar razonablemente.”

¿Un olmo que ya no está pero del que Holmes –y también el mayordomo– conoce su altura, además de las indicaciones dadas por el ritual? Las deducciones continúan:

“Miré el sol. Estaba bajo en el cielo, y calculé que en menos de una hora se situaría exactamente sobre las ramas más altas del viejo roble, y se cumpliría entonces una condición mencionada en el Ritual. Y la sombra del olmo había de referirse al extremo distante de la sombra, pues de lo contrario se habría elegido como guía el tronco. Por consiguiente, había de averiguar dónde se encontraba el extremo distante de la sombra cuando el sol estuviera exactamente fuera del árbol.

– Esto debió de ser difícil, Holmes, dado que el olmo ya no estaba allí

– Pero al menos sabía que, si Brunton pudo hacerlo, yo también podría. Además, de hecho no había dificultad. Fui con Musgrave a su estudio y me confeccioné esta clavija, a la que até este largo cordel, con un nudo en cada yarda. Cogí después dos tramos de caña de pescar, que representaban exactamente seis pies, y volví con mi cliente allí donde había estado el olmo. El sol rozaba ya la copa del roble. Aseguré la caña de pescar en el suelo, marqué la dirección de la sombra y la medí. Su longitud era de nueve pies.

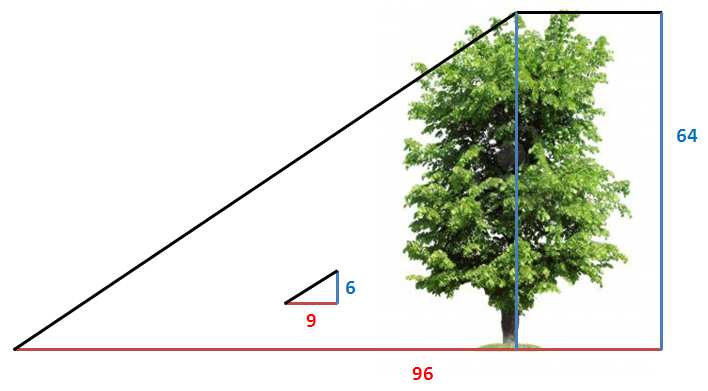
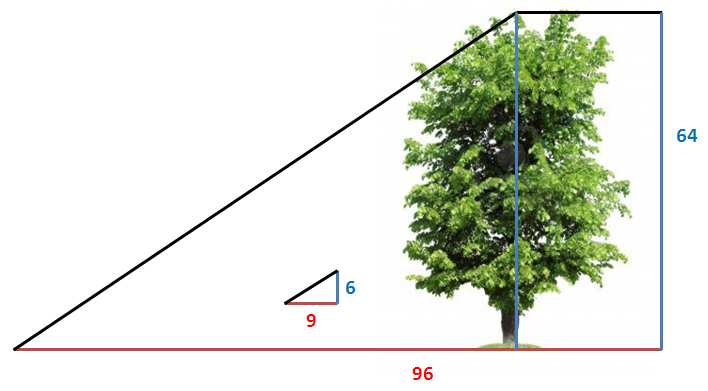
Desde luego, el cálculo era ahora de lo más sencillo. Si una caña de seis pies proyectaba una sombra de nueve, un árbol de sesenta y cuatro pies proyectaría una de noventa y seis, y ambas tendrían la misma dirección. Medí la distancia, lo que me llevó casi hasta la pared de la casa, y fijé una clavija en aquel punto.”

Tras encontrar el punto definido por la sombra –gracias al teorema de proporcionalidad de triángulos de Thales, perfectamente descrito por Holmes–queda por utilizar la última parte del ritual:

“Al norte por diez y por diez, al este por cinco y por cinco, al sur por dos y por dos, al oeste por uno y por uno, y por debajo.”

Siguiendo estas instrucciones, Holmes y Musgrave descubren una cava bajo la casa… y allí el cadáver del mayordomo –probablemente asesinado por la agraviada sirvienta, celosa de la nueva amante de Brunton– y la corona de los reyes de Inglaterra confiada a la custodia de la familia, y que por alguna razón el heredero del trono no había recuperado…

“– ¿De quién era?

– Del que se ha marchado.

– ¿Quién la tendrá?

– El que vendrá.”

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.