La conjetura de Goldbach
El pasado mes de mayo (de 2013) se difundió velozmente a través de la red que había sido demostrada la conjetura débil de Goldbach, llegando incluso a ser recogida la noticia por medios de comunicación más tradicionales, como por ejemplo el periódico ABC, “Un matemático peruano resuelve un problema de hace casi tres siglos”. La conjetura débil de Goldbach dice que…
“todo número mayor que cinco puede escribirse como
suma de tres números primos”.
El autor de la demostración de este problema abierto desde hace más de dos siglos y medio, es el matemático peruano Harald Andrés Helfgott (Centre National de la Recherche Scientifique – CNRS, París, Francia), quien colgó, el día 13 de mayo de 2013, su artículo Major arcs for Goldbach’s theorem en la base de preprints ArXiv, completando así su trabajo anterior, Minor arcs for Goldbach’s theorem.
Con este resultado parece que queda más cerca la posible resolución de la famosa conjetura (fuerte) de Goldbach,
“todo número par mayor que dos puede escribirse como
suma de dos números primos”
Pero intentemos empezar por el principio de esta historia, por su autor Christian Goldbach (1690-1764) y las conjeturas que llevan su nombre (la fuerte y la débil). Este matemático nació en la prusiana ciudad de Königsberg (actualmente Kaliningrado, perteneciente a Rusia) en 1690. Viajó mucho por Europa y conoció a matemáticos como Gottfried W. Leibniz, Leonhard Euler o Daniel Bernoulli. En 1725 se fue a trabajar de historiador y profesor de matemáticas a la recién creada Academia de las Ciencias de San Petersburgo, y 3 años más tarde se iría a Moscú para ser tutor de Pedro II de Rusia. Allí moriría en 1764, a la edad de 74 años.
La formulación de la llamada conjetura de Goldbach se gestó en la correspondencia entre el propio Goldbach y su amigo, el gran matemático suizo Leonhard Euler. En una carta de Goldbach a Euler, del 7 de junio de 1742, el autor de la misma le plantea una conjetura relacionada con los números primos, que simplificándola podría expresarse como que “todo número que se puede representar como suma de dos números primos, entonces se puede representar como suma de tres números primos.”
Así vemos que
6 = 3 + 3 = 2 + 2 + 2
7 = 5 + 2 = 3 + 2 + 2
8 = 5 + 3 = 3 + 3 + 2
9 = 7 + 2 = 5 + 2 +2 = 3 + 3 + 3
10 = 7 + 3 = 5 + 5 = 5 + 3 + 2
11 = 7 + 2 +2 = 5 + 3 + 3
y de paso, observamos que 11 no se puede escribir como suma de dos números primos, aunque sí de tres números primos. Luego, dos preguntas interesantes que rápidamente se nos ocurren relacionadas con esto serían ¿qué números se pueden escribir como suma de dos números primos? y ¿pueden todos los números ser escritos como suma de tres números primos?
En su respuesta, Euler le contesta que la conjetura de su carta sería cierta –y él tiene una demostración sencilla- si fuese cierta la observación que Goldbach le había hecho en una carta anterior “todo número par mayor que dos puede escribirse como suma de dos números primos” (¡y ahí tenemos la conjetura!)
Este fue el punto de inicio de lo que se ha dado en llamar la conjetura de Goldbach (o también la conjetura fuerte de Goldbach). Siendo la conjetura débil de Goldbach… “todo número mayor que cinco puede escribirse como suma de tres números primos”. Y la demostración que Euler mencionaba en su carta (podéis verla en el libro [1] de la bibliografía) establecería que si es cierta la conjetura fuerte, entonces es cierta la débil (que es el resultado que el matemático prusiano mencionaba en la carta de junio de 1742).
Por cierto, en esa misma carta Goldbach escribe lo siguiente…
“No creo que sea totalmente inútil plantear aquellas proposiciones que son muy probables aunque falte una verdadera demostración, pues aun cuando se descubra que son incorrectas, pueden conducir al descubrimiento de una nueva verdad.”
Esta es una reflexión muy interesante sobre las matemáticas en sí mismas. Pero vayamos de nuevo a la conjetura de Goldbach…
“todo número par mayor que dos puede escribirse como suma de dos números primos”
Podemos ver qué pasa con los primeros números…
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
16 = 3 + 13 = 5 + 11 …
… una primera cuestión que se observa es que esa descomposición, si existe, no es única… como puede observarse en los números 10, 14 o 16. Pero si observamos el número 22 este puede ser expresado de tres formas distintas, 22 = 11+11 = 17+5 = 19+3.
Como comentan Carlos Sánchez y Rita Roldán, en su libro “Goldbach, una conjetura indomable”, un método para ver si un número, por ejemplo el 22, se puede descomponer como suma de dos números primos sería poner dos filas una con los números del 1 hasta la mitad del número (en nuestro caso el 11, que es la mitad de 22) y otra fila del número menos 1 (en nuestro ejemplo, 21) hasta la mitad (de nuevo, 11), de forma que cada columna suma siempre el número (en nuestro caso el 22)…
| Primera fila | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Segunda fila | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 |
| Suma | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
Ahora, como en la criba de Eratóstenes para los números primos, se tachan las columnas con números compuestos (es decir, no primos), quedando únicamente las sumas con factores primos. Y para el 22 nos quedaría que como habíamos comentado anteriormente…
22 = 3 + 19 = 5 + 17 = 11 + 11
Pero este método empieza a ser un mal método para los números grandes, y además podrá ser útil para saber si un número par en concreto se puede escribir como suma de dos primos, pero no resuelve para nada la conjetura.
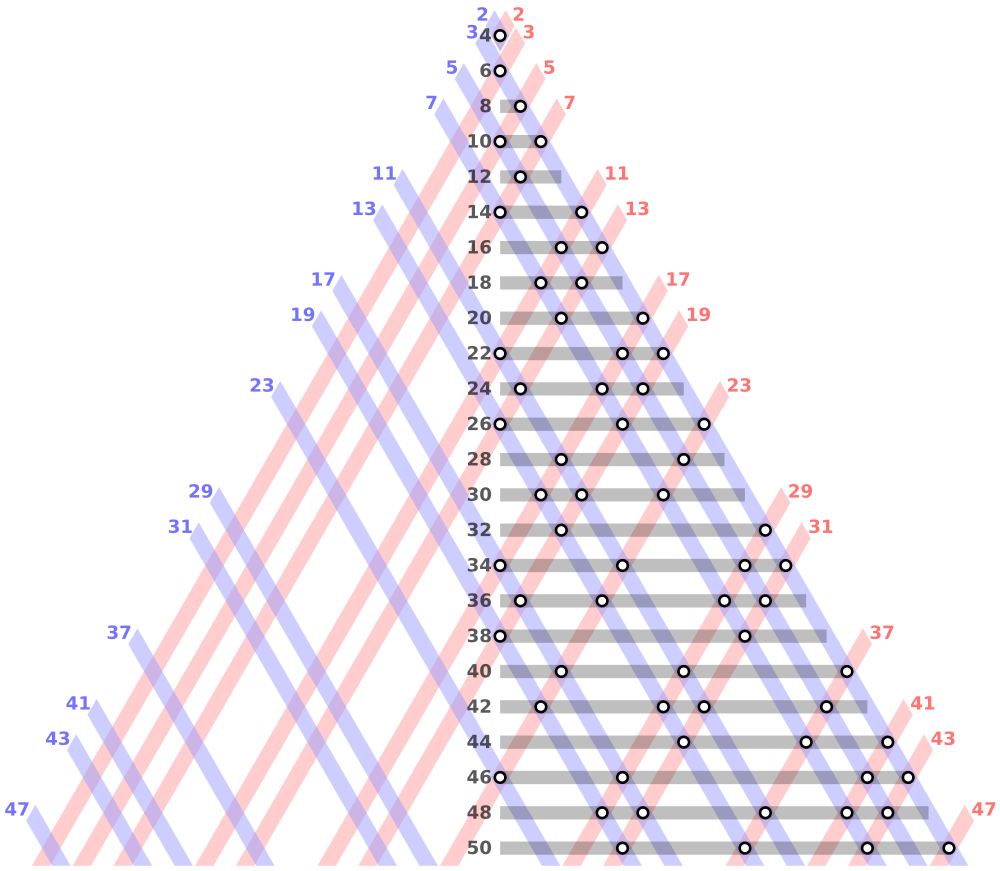
Otro posible método podría ser plantearlo al revés, es decir, coger todas las sumas de dos números primos (empezando por abajo, 2, 3, 5, 7,…) y ver si recorren todos los números pares. Aunque este nos conduce a otro problema complejo sobre la distribución de los números primos…
Desde su formulación este problema (conocido hoy como la conjetura de Goldbach) ha interesado, además de a Euler, a muchos grandes matemáticos como Georg Cantor, Lev Schnirelman, Geoffrey H. Hardy o Ivan Vinogradov, entre muchos otros, lográndose grandes avances (tanto en la conjetura fuerte, como en la débil) pero sin conseguir la tan ansiada demostración del mismo.
Entre los avances que se han conseguido están:
A. La comprobación de la conjetura hasta números pares muy grandes, para lo cual se han utilizado algoritmos eficientes y ordenadores potentes, en particular,…
| Autor | año | límite superior |
| A. Desboves | 1855 | 10.000 |
| N. Pipping | 1940 | 100.000 |
| M. K. Shen | 1964 | 3,3 ´ 107 |
| Stein – Stein | 1965 | 108 |
| A. Granville etal. | 1989 | 2 ´ 1010 |
| … | … | … |
| Richstein | 2001 | 4 ´ 1014 |
| … | … | … |
| Oliveira e Silva | 2008 | 12 ´ 1017 |
¡¡ en 2012 se comprobó hasta el número 4 x 1018
(es decir, números con 19 cifras) !!
Aunque el avance computacional no resuelve por sí solo el problema, ya que hay infinitos números.
B. También se ha demostrado que la conjetura de Goldbach es cierta para casi todos los números pares, que en este contexto matemático, esta expresión quiere decir que el límite del cociente entre el número de pares menores que m para los que se cumple la conjetura y el número de todos los pares menores que m, es igual a 1 (cuando m tiende a infinito). Intuitivamente, podríamos decir, que para números pares muy, muy grandes, sería raro que no se cumpliera la conjetura.
C. Otro resultado interesante que se ha conseguido probar es que todo número par puede escribirse como suma de, como mucho, 6 primos. (Olivier Ramaré, CNRS, Université des Sciences et Technologies de Lille.)
D. Y por último, como decíamos al principio del artículo, este mismo año 2013 el matemático peruano Harald Andrés Helfgott ha conseguido demostrar la conjetura débil de Goldbach… recordemos que “todo número mayor que cinco puede escribirse como suma de tres números primos”. Y la resolución de la conjetura débil de Goldbach implica un resultado relacionado con la conjetura fuerte, y es que todo número par puede expresarse por tanto como suma de, como mucho, 4 primos.
Para terminar vayamos brevemente a la presencia de la conjetura de Goldbach en la cultura. En el año 2000 se publicaría en varios países la novela “El tío Petros y la conjetura de Goldbach” del griego Apostolos Dioxiadis, que tenía como uno de sus elementos principales la conjetura de Goldbach, puesto que el tío Petros era un matemático que en su tiempo había intentado demostrarla. Para dar publicidad a esta novela, las editoriales Faber and Faber (inglesa) y Bloomsbury (americana) ofrecieron un premio de un millón de dólares para quien resolviera este problema matemático antes de abril de 2002, pero nadie reclamó el premio…
Esta conjetura aparece también en las películas La habitación de Fermat (película española de 2007, dirigida por Rodrigo Sopeña y Luis Piedrahita… al principio de la película se explica la conjetura, y uno de los protagonistas va a presentar una demostración… ) y la Verdad Oculta (de 2005, dirigida por John Madden, y basada en la magnífica obra de teatro Proof de David Aurburn), y se menciona en la segunda película de Futurama (la bestia de un millón de espaldas)…
[https://www.youtube.com/watch?v=GjElx-fZX8s]
Bibliografía:
[1] Carlos Sánchez y Rita Roldán, Goldbach, Una conjetura indomable, Nivola, 2009.
[2] Javier Cilleruelo Mateo, La conjetura de Goldbach, La Gaceta de la RSME, volumen 3, n. 3, 2000.
[3] Entrevista a Harald Andrés Helfgott, realizada por Juanjo Rué y Ágata A. Timón (ICMAT), para el blog “Matemáticas y sus fronteras”
Sobre el autor: Esta anotación ha sido realizada por Raúl Ibáñez, profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica





La conjetura de Goldbach | Mates_mv | Scoop.it
[…] El pasado mes de mayo (de 2013) se difundió velozmente a través de la red que había sido demostrada la conjetura débil de Goldbach, llegando incluso a ser recogida la noticia por medios de comunica… […]
Luis GSA
No he podido leer en ninguna parte un asomo de respuesta a mi pregunta a mí mismo desde hace mucho: ¿por qué diablos nadie se refiere jamás a la conjetura de Golbach bajo su forma claramente equivalente “todo entero mayor que 4 equidista de dos primos”? Me parece tan bonito y sugerente este enunciado que me extraña mucho que nadie lo pronuncie. A veces he llegado a pensar que debo estar equivocado con esa evidente equivalencia.
Rbl
Si es cierta la conjetura de Goldbach cualquier numero entero es equidistante a dos primos.
Me
La conjetura habla de números pares, no te todos los enteros… c:
Ricardo Gutiérrez.
Perdonen mi ignorancia pero estoy de acuerdo con Luis GSA, porque se trata de una expresión muy interesante. Mi pregunta concreta es: ¿Por qué una conjetura es equivalente a la otra?
Lo Mejor de la Semana (23-29 de junio) | Hablando de Ciencia | Artículos
[…] La historia completa de la conjetura de Goldbach. […]
Ramón Ruiz
Una demostración de la conjetura de Goldbach con un planteamiento original y con unas pocas fórmulas muy sencillas se puede ver en: http://viXra.org/abs/1406.0026
dolores bermudo
Siempre he estado obsesionada con losnumeros primos. Lagran ilusion de mi vida con la a muchas noches he soñado es descubrir la teoria de lo numeros primos. Quizas en la otra vida lo logre.
La conjetura de Goldbach |
[…] artículo La conjetura de Goldbach de Raúl Ibáñez Torres (Departamento de Matemáticas, ZTF-FCT) se publicó en el blog Cuaderno de […]
Uno que pasaba por aquí
Si consideramos conocidos los números pares en el intervalo (0,n) y puramente aleatorios y que cumplen la ley de los números primos a los números primos comprendidos en el intervalo (n,2n), podemos plantear el problema de la siguiente manera:
2n=3+impar1 2n=5+impar2 2n=7+impar3 2n=primo+imparn
De está forma se ven claramente dos cuestiones:
1) La probabilidad de que uno de nuestros impares sea primo es cada vez más pequeña, pero nunca es cero. Y gracias a la ley de los números primos sabemos cuantos números primos tenemos aproximadamente en el intervalo (n,2n)
2) El número de comprobaciones a realizar es cada vez mayor. ¿La sufiente?
En una analogía sencilla, los números primos conocidos son los boletos de lo lotería que hemos comprado. Y los números primos por descubrir, los premios.
Pero no estamos hablando de que nos toque el gordo, estamos hablando de que nos toque la pedrea del sorteo de Navidad…
Todo el mundo sabe cuantos boletos hay que comprar para que te toque la pedrea del sorteo de Navidad, pero, ¿Y si cambian las condiciones del sorteo un poquito?
Una vez que te ha tocado un sorteo, la única forma de que te vuelva a tocar seguro es comprar un número de billetes suficiente para compensar la caída de la probabilidad.
Si esto lo hacemos para cada 2n, donde la probabilidad cae de forma fija y conocida, lo que tenemos es un problema de cálculo.
La derivada de la función cantidad de números primos crece al mismo ritmo que desciende la probabilidad, y por tanto, ambos efectos se compensan… Es decir, en todo momento estamos comprando boletos al mismo ritmo que bajan las probabilidades de que nos toque. Y como nos ha tocado el primero, nos tocan todos.
Todo esto se aprecia muy bien en el cometa. Lo que tenemos es la representación de un montón de sorteos donde toca de forma segura un mínimo o más. Por eso se aprecia un mínimo, no hay excepciones, o no se pasa de 50 formas a 1000 y de nuevo a 10 en un intervalo.
Los números de la suerte — Cuaderno de Cultura Científica
[…] de la suerte. La conocida conjetura de Goldbach (sobre la que podéis leer más en la entrada La conjetura de Goldbach) nos dice […]