El físico Niels Bohr nació el mismo año en el que el matemático y maestro Johann Jakob Balmer publicó una fórmula (ver [1]) que asombró a la comunidad científica, y que el propio Bohr consiguió esclarecer veintiocho años más tarde.

En 1882, una vieja iglesia en Basilea (Suiza) –cerca de la casa de Balmer– comenzaba sus reformas. El maestro, prácticamente jubilado, se entretenía midiendo las proporciones del edificio. La razón de anchura entre altura, anchura entre longitud, y longitud del coro entre longitud de la nave eran, respectivamente, 2/7, 3/7 y 5/9.

Balmer estaba dando vueltas a un pequeño enigma que le acababa de proponer su amigo, el físico Eduard Hagenbach-Bischof: el espectro visible del hidrógeno está formado por cuatro líneas luminosas –llamadas hoy en día series de Balmer– cuyo orden obedece una regla.

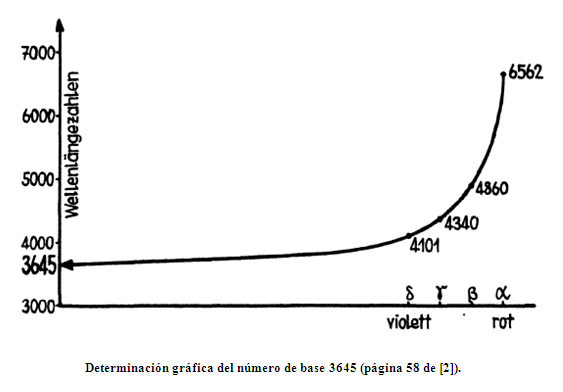
Los números 6562, 4860, 4340 y 4101 representan, en ångström, las longitudes de onda de la luz visible emitida por el hidrógeno.

Si se aplica la razón 5/9 –la razón más grande obtenida en la iglesia– a la mayor de las longitudes de onda, se obtiene el número 3645, a partir del cual pueden obtenerse las otras tres longitudes al multiplicar por 16/12, 25/21 y 36/32:

1. 3645 x 9/5 = 6562,
2. 3645 x 16/12 = 4860,
3. 3645 x 25/21 = 4340, y
4. 3645 x 36/32 = 4101.

Pero aún hay más: 9/5 = 9/(9-4), y si se escribe en términos de cuadrados, se obtiene:

1. 9/5 = 3²/(3²-2²)
2. 16/12 = 4²/(4²-2²)
3. 25/21 = 5²/(5²-2²)
4. 36/32 = 6²/(6²-2²)

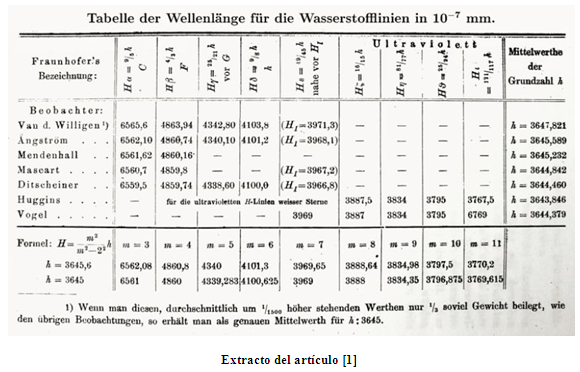
La fórmula de Balmer –obtenida por el maestro de manera empírica– para la longitud de onda λ de las líneas espectrales visibles del átomo de hidrógeno es:

donde n = 2, h = 3645 ångström, y m es un entero mayor o igual a 3.

En su artículo [1], Balmer denomina h –llamada hoy en día la constante de Balmer– ‘número fundamental del hidrógeno’.

Según Hagenbach, Balmer no era (ver [3]):

ni un matemático inspirado, ni un experimentador sutil, sino un arquitecto. […] Para él, el mundo, la naturaleza y el arte estaban en una armonía unificada, y el objetivo de la vida era encontrar la expresión numérica de estas relaciones armónicas.

La formula de Balmer fue una incógnita durante 28 años. Se descubrieron otras líneas espectrales del hidrógeno, que se integrarían perfectamente en la fórmula; otros físicos la completaron y refinaron, pero ninguno fue capaz de explicar la razón por la que el átomo de hidrógeno produce una luz tan simple aritméticamente.

En 1913, Niels Bohr pensaba que el modelo del átomo de Rutherford no tenía sentido. A principios de febrero, un colega le mostró la fórmula de Balmer, que Bohr decía no conocer. Apenas un mes más tarde publicó el artículo revolucionario en el que presentaba el modelo atómico de Bohr: “En cuanto vi la fórmula de Balmer, todo se me apareció inmediatamente claro.” (ver [3]). Bohr fue capaz entonces de explicar de forma teórica la fórmula de Balmer, de explicitar todos sus términos. Por ejemplo, el misterioso ‘número fundamental del hidrógeno’, se obtiene combinando varias constantes físicas –entre ellas la masa y la carga del electrón–.

El físico León Rosenfeld escribiría (ver [3]):

Asistimos a un increíble proceso creativo, en el cual, una vez puesta la última pieza del puzle [la fórmula de Balmer], todo el saber que Bohr había acumulado, todas sus hipótesis sobre la estructura del átomo cristalizan y repentinamente se colocan perfectamente en su lugar, proporcionándole una vista completa de conjunto.

Referencias:

[1] Johann Jakob Balmer, Notiz über die Spektralliniendes Wasserstofs, Annalen der Physik 25, 80-87, 1885.

[2] Heinz Balmer, Johann Jakob Balmer, Elemente der Mathematik 16 (3), 49-60, 1961.

[3] Nicolas Witkowski, Une histoire sentimentale des sciences, Seuil, 2003.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Esta anotación participa en la edición LI del Carnaval de la Física cuyo blog anfitrión es ::ZTFNews y en la Edición 5.3: Felix Klein del Carnaval de Matemáticas cuyo anfitrión es Juegos Topológicos.