El problema de Molyneux (ver [3]) es un experimento mental planteado por el filósofo William Molyneux a John Locke: en él se especula sobre la reacción que tendría un ciego de nacimiento al recuperar la vista de adulto. Si mirara un cubo y una esfera –figuras geométricas que reconocía gracias al sentido del tacto–, ¿distinguiría con la mirada lo que ya sabía identificar con las manos?

Molyneux expuso por vez primera este dilema en su trabajo Dioptrica nova, planteándolo en forma de problema a John Locke en una carta del 2 de marzo de 1693:

Soy de la opinión de que el ciego no podría, a primera vista, decir con certeza cuál es el globo y cuál el cubo, mientras sólo los viera, aunque por el tacto pudiera nombrarlos sin equivocarse y con toda seguridad supiera distinguirlos por las diferencias de sus formas tentadas.

El problema fue muy controvertido, aunque parece que Molyneux tenía razón en parte, según aseguran recientes estudios (ver [1]).

El matemático Alexei Sossinsky (1937-) insiste en esta idea; puede leerse en la página 37 de [7] –traducido del francés por la autora de esta anotación–:

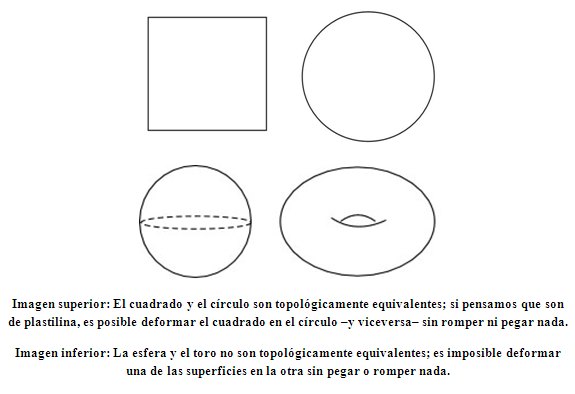
[…] al igual que no es nada sorprendente el hecho de que casi todos los matemáticos ciegos son (o han sido) geómetras. La intuición del espacio que tenemos el resto de nosotros, los que vemos, está sobre todo basada en la imagen del mundo que se proyecta sobre nuestra retina; es por lo tanto una imagen en dos (y no en tres) dimensiones la que nuestro cerebro analiza. La intuición del espacio de un invidente, por el contrario, proviene sobre todo de una experiencia táctil y operacional. ¡Es mucho más profunda, en el sentido propio como el figurado! […] Para terminar esta digresión, notemos que trabajos biológico-matemáticos bastante recientes (basados en en estudio de niños y adultos nacidos ciegos y habiendo recuperado la vista después) han probado que las estructuras matemáticas más profundas, por ejemplo las estructuras topológicas, son innatas, mientras que las estructuras más finas, como las estructuras lineales, son adquiridas. […] Así, un ciego recuperando la visión no distingue, al principio, el cuadrado del círculo: sólo ve su equivalencia topológica. Sin embargo, ve también que el toro no es una esfera. En cuanto a nosotros, nuestra tendencia a hacer absoluto lo que vemos nos hace a menudo concebir el mundo de una manera más bien plana y superficial.

Ha habido –y hay– efectivamente, muchos matemáticos ciegos: he elegido cuatro de ellos para ilustrar las anteriores opiniones.

1. Nicholas Saunderson (1682-1739) perdió la vista al enfermar de viruela con tan solo un año. Su ceguera le permitió adquirir un excepcional sentido del oído y del tacto y una increíble agilidad mental para los cálculos matemáticos (ver [4]).

2. Leonhard Euler (1707-1783) tuvo graves problemas de vista, y quedó ciego los últimos diecisiete años de su vida. Sin embargo, su producción matemática no se vio afectada.

3. Louis Antoine (1888-1971) perdió la vista en 1917 debido a una herida sufrida durante la guerra. Sus contribuciones a la topología en dimensión 3 fueron fundamentales, construyendo un bellísimo ejemplo de conjunto de Cantor en el espacio tridimensional, el collar de Antoine. ¿Cómo pudo ‘visualizar’ y construir un objeto tan complejo? (ver [5]).

4. Lev Semenovich Pontryagin (1908-1988) perdió la vista con 14 años debido a la explosión de una estufa; a pesar de ello se convirtió en uno de los grandes matemáticos del siglo XX, realizando importantes contribuciones en topología algebraica y diferencial (ver [6]).

¿Habrían conseguido los mismos éxitos científicos con una visión normal?

Referencias:

[1] Richard Held, Yuri Ostrovsky, Beatrice de Gelder, Tapan Gandhi, Suma Ganesh, Umang Mathur and Pawan Sinha, The newly sighted fail to match seen with felt, Nature Neuroscience 14 (2011) 551–553

[2] Allyn Jackson, The World of Blind Mathematicians, Notices of the AMS vol. 49, no. 10 (2002) 1246-1251

[3] Marta Macho Stadler, El problema de William Molyneux, ::ZTFNews, 2013

[4] Marta Macho Stadler, Nicholas Saunderson, extraordinario calculador, ::ZTFNews, 2013

[5] Marta Macho Stadler, Louis Antoine y su fabuloso collar, ::ZTFNews, 2013

[6]Marta Macho Stadler, Pontryagin, un genio matemático a pesar de su ceguera, ::ZTFNews, 2013

[7] Alexei Sossinsky, Noeuds. Genèse d’une théorie mathématique, Seuil, París, 199

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.