La triscaidecafobia es el miedo al número 13 y la parascevedecatriafobia es el temor irracional al viernes y 13 –no tan arraigado en nuestra cultura, pero si en la anglosajona–.

A pesar de los ejemplos que podamos recordar de variadas tragedias ocurridas en viernes y 13, ¿tiene algún fundamento lógico la parascevedecatriafobia? ¿Tienen algo de especial los viernes y 13? Vamos a ver que, realmente, son singulares en cierto sentido.

El calendario gregoriano –el que utilizamos– posee una característica notable: es periódico. Su período es de 400 años, es decir, en ese momento comienza exactamente la misma secuencia de días, semanas y meses.

El calendario gregoriano distingue entre años comunes –de 365 días–, años bisiestos –de 366 días–, y años seculares –terminados en 00–.

Un año es bisiesto si es múltiplo de 4, exceptuando los años seculares que no sean múltiplos de 400. Por ejemplo, 1900 y 2100 no son bisiestos porque no son divisibles por 400 –aunque sean múltiplos de 4–; sin embargo, 2000 sí lo es. Así, en un período de 400 años, hay 100-3=97 años bisiestos.

¿Cuántos días hay en 400 años? Son

(97 x 366) + (303 x 365) = 35.502 + 110.595 = 146.097.

El número 146.097 es múltiplo de 7 (146.097 = 7 x 20.871): hay 20.871 semanas en un período de 400 años. Cada uno de los 4.800 meses que conforman esos 400 años posee un día 13: pero 4.800 no es divisible por 7 (4.800/7=685,713), por lo que deducimos que no puede haber la misma cantidad de días de la semana que caigan en 13.

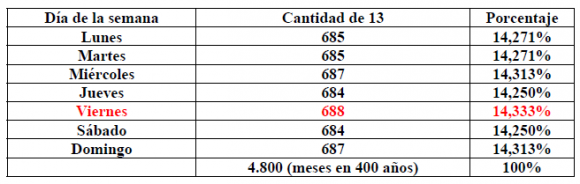
El profesor de matemáticas B. H. Brown (Darmouth) demostró (ver [2]) que el día 13 cae más veces en viernes que cualquier otro día de la semana. La distribución de los días 13 de cada mes –en un ciclo de 400 años– se resume en la siguiente tabla:

Efectivamente, los viernes y 13 son especiales, su porcentaje de aparición es ligeramente superior al del resto de días 13. Brown hizo su cálculo a mano, con un poco de paciencia; pero existen programas que permiten comprobar estos datos, por ejemplo el dado en [3].

Referencias:

[1] Calendario gregoriano

[2] B. H. Brown, Solution to Problem E36, American Mathematical Monthly 40 (1933) 607.

[3] Friday the Thirteenth, Wolfram Research

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Esta entrada participa en la Edición 5.4: Martin Gardner del Carnaval de Matemáticas cuyo anfitrión es Gaussianos